Контроль и ревизия конспект лекций

Задача 4. Решение

Задача 3. Решение

Задача 2. Решение

Задача 1. Решение

Таблица 1.

Записать итоговый результат Rрасч обработки.

Сравнить в графической форме эмпирическую F_e (DR_к) и теоретическая F(R) функция распределения

a_ф = 0.5 (варианты 1…10), a_ф = 0.7 (варианты 11…20).

i
Ri, Ом	11.368	11.364	11.383	11.349	11.339	11.357	11.347	11.355
i
Ri, Ом	11.376	11.359	11.356	11.348	11.367	11.362	11.363

а) Располагаем значения (R_i) в порядке возрастания

i
Ri, Ом	11.339	11.347	11.348	11.349	11.355	11.356	11.357	11.359
i
Ri, Ом	11.362	11.363	11.364	11.367	11.368	11.376	11.383

б) Делим диапазон D = R_max - R_min на шесть равных интервалов с границами (DR_к)

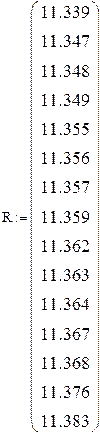
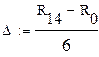
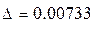
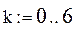
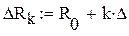
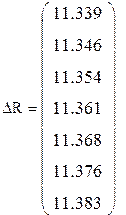
Границы

Определяем n_к – число измерений, приходящиеся на интервалы

(k = 0 … 5)

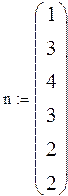
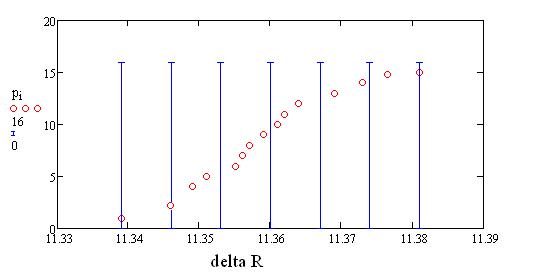
Иллюстрация Правила включения точек, лежащих на границе интервала (включение в интервал точки, лежащей на левой границе)

в) Рассчитываем локальную вероятность P_к = n_к / N для каждого к – интервала. Решающую функцию назначаем в следующем виде: вдолю n_k включаются все точки + левая граница из k – интервала; в последнюю группу (k= 5) включается точка правой границы.

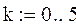
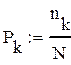
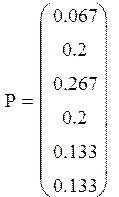
Строим гистограммы:

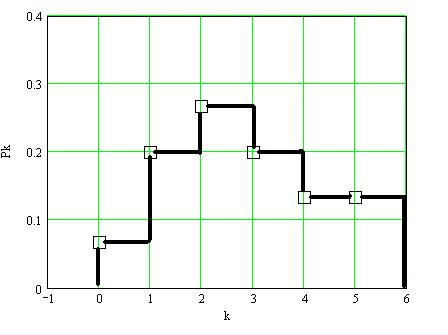
Рис. 1. Гистограмма P_i (ΔR_k)

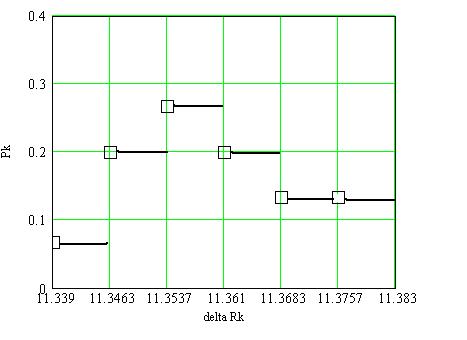
Рис. 2. Гистограмма P_i (ΔR_k)

г) Рассчитываем эмпирическую плотность вероятности f_к для интервала (к = 3)

(1/Ом)

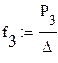
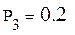
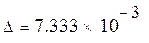
а) Вычисляем эмпирическую функцию распределения F_e (DR_к) в заданных точках

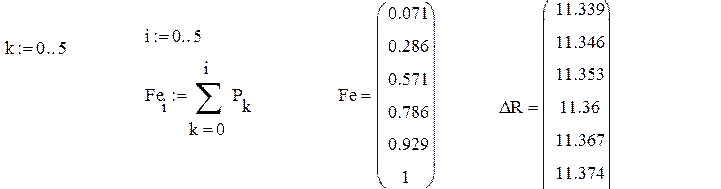
б) Строим эмпирическую функцию распределения F_e (DR_к)

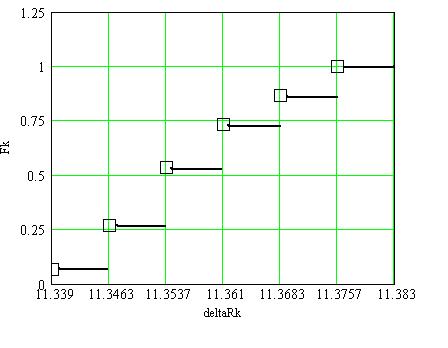
Рис. 3. Эмпирическая функция распределения F_e (DR_к)

а) Оцениваем параметры A, D и s, приняв гипотезу нормального распределения:

X = R = (R_i)Î N (A,s ² ).

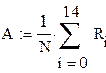
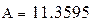Ом

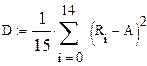
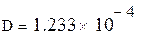
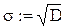
Ом

б) Определяем фиксированные значения z _ф – относительные отклонения для точек

R = (R _ср, R _ср+ s, R _ср + 2 s, R _ср + 3 s):

z _{ф i} = (R_i - R _ср)/ s = (0, 1, 2,3), i = 0… 3.

Определяем функцию Лапласа Ф_i в заданных точках (i = 0…3) (Рабинович С.Г., Погрешность измерений, Табл. П1 и П2 (стр. 246, 247))

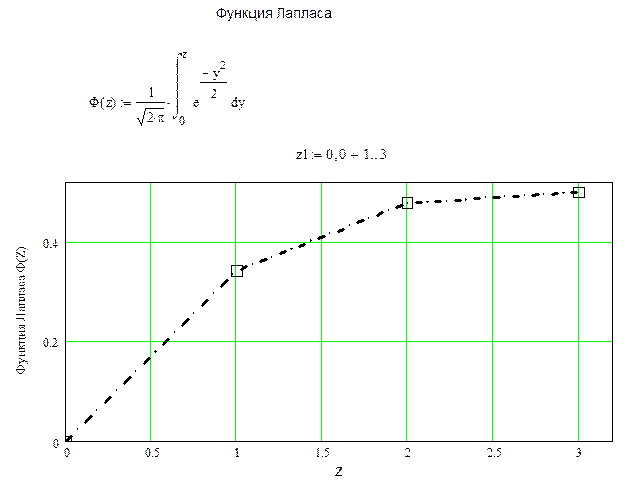
Рис. 4. Функция Лапласа Ф_i

в) Определяем значения теоретической функции распределения F_i при i = -3…+3 в фиксированных точках. Используя (z _{ф i}, Ф_i), вычисляем фиксированные аргументы X_fi и F_{f i} при R ≥ R _ср (i = 0…3)

X_fi = R _ср + z _{ф i}s =

= (R _ср, R _ср+ s, R _ср + 2 s, R _ср + 3),

F_{f i} = 0.5 + Ф_i .

Вычисляем фиксированные аргументы X_{f i} и F_{f i} при R < R _ср
(i = - 1…-3)

X_{f (- i )} = R _ср – z _фis =

= (R_ср – s, R _ср – 2 s, R _ср – 3 s),

F_{f (- i)} = 0.5 - Ф_i .

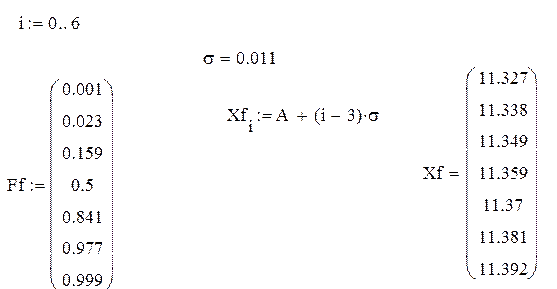
г) Строим теоретическую функцию распределения F в точках X_{f i}

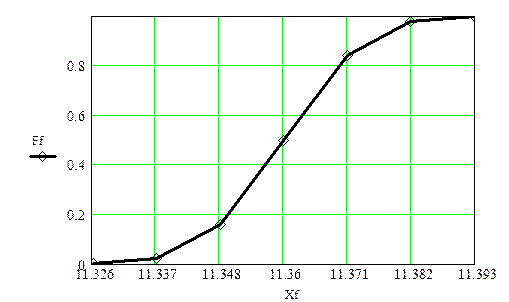
Рис. 5. Теоретическая функция распределения F

а) Определяем доверительный интервал D _ф случайной погрешности для индивидуального результата при условии, что доверительная вероятность задана как a_ф = 0.5.

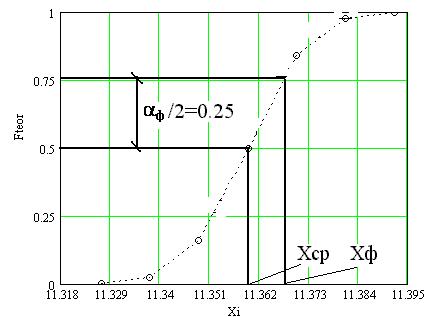
Рис. 6. Фиксированные интервалы

б) вычисляем: F _ф = 0.5 + a_ф/2 = 0.75; Х _ф(F _ф) = 11.670; определяем допуски

D _ф(R) = Х _ф - Х _ср = 0.011 Ом, d _случ(R) = D _ф/ Х _ср = 0.1%.

в) записываем ответ для индивидуального результата измерения

R _расч = А± D _ф = Х _ср ± D _ф = (11.670± 0.011) Ом при a_ф = 0.5.

г) строим функции распределения: экспериментальную F_e (DR_к) и теоретическую F(R) на одном графике

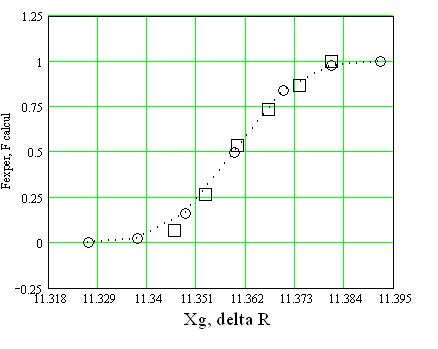
Рис. 7. Варианты функции распределения

□– Fexper, эмпирическая функция распределения,
○– Fcalcul, теоретическая функция распределения.