2014-02-02
697
| Значение r | Характер связи | Интерпретация связи |
| r = 0 | Отсутствует | Изменение x не влияет на изменения y |
| 0 < r < 1 | Прямая | С увеличением x увеличивается y |
| -1 > r > 0 | Обратная | С увеличением x уменьшается y и наоборот |
| r = 1 | Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного |
Значимость линейного коэффициента корреляции проверяется на основе t- критерия Стьюдента. Для этого определяется фактическое значение критерия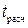 
:
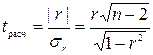, (6.3)
Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
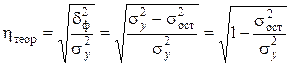, (6.4)
где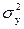 
– общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;
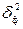– факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;
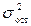– остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.
По правилу сложения дисперсий:
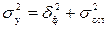, т.е. 
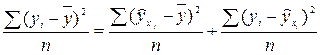. (6.5)
Оценка связи на основе теоретического корреляционного отношения проходил по шкале Чэддока (тема 4).
Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = | r|.
Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками.
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
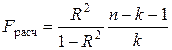, (6.7)
где R 2 – коэффициент множественной детерминации (R 2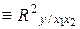 
);
k – число факторных признаков, включенных в уравнение регрессии.
ТЕМА 7. Ряды динамики
