Таблица 7.1 Уровни (показатели) ряда динамики
Анализ динамических рядов
Динамический ряд представляет собой хронологическую последовательность числовых значений статистических показателей.
Виды рядов динамики (РД):
1) моментные (моментальные) РД;
2) интервальные РД;
3) РД с нарастающими итогами;
4) производные РД.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности.
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями в результатах развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяца, квартала, года и т.д.).
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные.
Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики:
- характеристика уровней развития изучаемых явлений во времени;
- измерение динамики изучаемых явлений посредством системы статистических показателей;
- выявление и количественная оценка основной тенденции развития (тренда);
- изучение периодических колебаний;
- экстраполяция и прогнозирование.
| Показатель | Формула | |
| Базисные | Абсолютный прирост | Δ = yi – у 0 (7.1) = yi – у 0 (7.1)
|
| Темп роста | 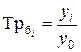 (7.2) (7.2)
| |
| Темп прироста | 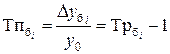 (7.3) (7.3)
| |
| Цепные | Абсолютный прирост | Δ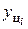 = yi – yi -1 (7.4) = yi – yi -1 (7.4)
|
| Темп роста | 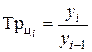 (7.5) (7.5)
| |
| Темп прироста | 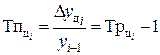 (7.6) (7.6)
| |
| Абсолютное значение 1% прироста | 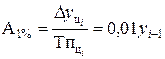 (7.7) (7.7)
| |
| Средние | Абсолютный прирост | 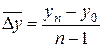 = = 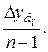 (7.8) (7.8)
|
| Темп роста | 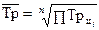  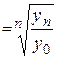 (7.9) (7.9)
| |
| Темп прироста | 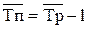 (7.10) (7.10)
|
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
Средний уровень интервального ряда определяется по формуле средней арифметической простой:
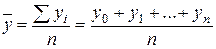 , (7.11)
, (7.11)
где n – число уровней.
В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:
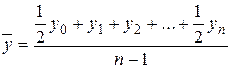 . (7.12)
. (7.12)
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:
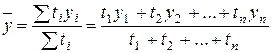 , (7.13)
, (7.13)
где уi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti.
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
 ;
;  . (7.14)
. (7.14)
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. Методы выявления тренда:
1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
2) Метод скользящей средней заключается в том, что исчисляется средней уровень из определенного числа (обычно нечетного) первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы “скользит” по ряду динамики, передвигаясь на один срок.
Сглаженный ряд урожайности по трехлетиям короче фактического на один элемент ряда в начале и в конце ряда.
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени.
Общая тенденция развития рассчитывается как функция времени:
ŷt = f (t), (7.15)
где ŷt – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней ŷt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a 0, a 1 – параметры уравнения; t – время):
Линейная функция (прямая) ŷt = a 0 + a 1· t. (7.16)
Показательная функция  . (7.17)
. (7.17)
Степенная функция (парабола) ŷt = a 0 + a 1· t + a 2· t 2. (7.18)
 2014-02-02
2014-02-02 520
520








