Аналитический метод

Методы решения уравнения движения поезда.

Анализ уравнения движения поезда.

Чтобы решить уравнение движения поезда, нужно найти удельные ускоряющие и замедляющие силы, которые определяют из удельных сил тяги, удельных сил сопротивления движению и удельных тормозных сил во всех диапазонах скоростей движения.

При движении поезда ускоряющая сила изменяется в связи с изменением режимов работы локомотива, плана и профиля пути. Наиболее общим случаем является ускоренное или замедленное движение и только в частных случаях – равномерное.

Ускоренное движение можно получить как в режиме тяги, так и в режиме выбега и торможения при следовании на спусках, когда составляющие от веса поезда окажутся больше сил сопротивления движения или суммы сил сопротивления движения и тормозной силы.

Равномерное движение наступает при равенстве этих сил.

Замедленное движение может быть и в режиме тяги при следовании по подъему, когда сила тяги окажется меньше сил основного и дополнительного сопротивлений движению.

При решении уравнения движения поезда определяют скорости движения, путь пройденный поездом за любой промежуток времени или время, необходимое для прохождения отрезков пути, в том числе и перегонов.

1) f_y > 0 – ускоренное движение, f_y = const > 0 равноускоренное

2) f_y < 0 – замедленное движение, f_y = const < 0 равнозамедленное

3) f_y = 0 – равномерное движение

Уравнение движения поезда:

для режима тяги: a = 120(f_k - ω₀ - ω_д)

для режима выбега: a = 120(- ω₀ - ω_д)

для режима механического торможения: a = 120(- в _т- ω₀ - ω_д)

Используются три метода решения уравнения движения поезда:

1. Аналитический.

2. Метод установившихся скоростей.

3. Графический.

При решении уравнения движения поезда любым способом необходимо иметь диаграмму удельных ускоряющих и удельных замедляющих сил.

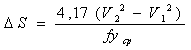
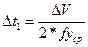
Принимается определенный интервал скорости Δ V, пусть равный 10 км/ч. В каждом интервале скорости от 0 до 10 км/ч, от 10 до 20 км/ч и так далее по диаграмме удельных ускоряющих и удельных замедляющих сил определяем f_{y ср}. Например, в интервале от 10 до 20 км/ч (Н/кН), затем необходимо учесть величину уклона данного профиля пути, при ξ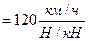 подсчитываем:

Аналогичным способом подсчитывают для другого профиля пути. Далее все Δ t складываем и находим время, например, для разгона поезда. Складывая всеΔ S, определяется путь, проходимый, например, при разгоне поезда.

С учетом полученных данных Δ V, Δ t, Δ S можно построить графические зависимости V (S) и t (S).