Общая модель парной регрессии

ЛЕКЦИЯ №4

После того, как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными, обычно переходят к математическому описанию конкретного вида зависимостей с помощью регрессионного анализа. С этой целью подбирают класс функций, связывающих результативный показатель 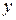и аргументы 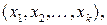отбирают наиболее информативные среди них аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют точность полученного уравнения.

Основная модель регрессии − это модель парной или однофакторной регрессии, которая называется полиномом первой степени.

Модель парной регрессии применяется для характеристики процессов, равномерно развивающихся во времени.

Допустим - доход семьи, 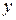- расход на питание.

Общий вид модели парной регрессии:

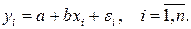(1)

где 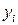- результативная (объясняемая, зависимая) переменная; 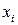- факторная (объясняющая, независимая) переменная или регрессор. Так же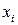- неслучайная (детерминированная) величина; 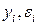- случайные величины; 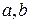- неизвестные параметры модели парной регрессии, которые необходимо найти, 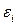- случайная ошибка регрессионной модели.

Уравнение (1) − регрессионное уравнение. Случайная ошибка модели парной регрессии возникает на основе объективных условий таких как:

1. условия нерепрезентативной выборки, при которой в парную регрессионную модель включается только один фактор, не способный полностью объяснить изменение результативной переменной;

2. условия ошибочного измерения переменных, участвующих в регрессионной модели;

3. агрегирование переменных;

часто рассматриваемая зависимость (1) − это попытка объединить вместе некоторое число макроэкономических явлений. Например, функция суммарного потребления есть выражение совокупности решений отдельных индивидов о расходах. Ясно, что эта функция неточна.

Агрегированная переменная – комплексная величина, поскольку концентрирует в себе совокупные результаты.

В макроэкономике рассматриваются следующие агрегированные экономические переменные: совокупный выпуск, потребление, инвестиции, импорт, экспорт;

4. неправильная спецификация.

Модель может иметь вид: 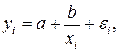или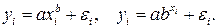

Примеры регрессионной модели (1).

1. Темпы инфляции в экономике 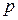(%), вызванные ростом зарплаты (%):

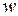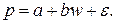
2. 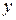- величина спроса на какой либо товар, 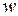- доход: 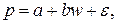где - случайная величина с некоторой функцией распределения вероятности.

Параметр 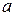в модели парной регрессии − это среднее значение зависимой переменной 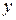при условии, что независимая переменная равна нулю (если значения 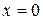имеет экономический смысл). Параметр 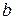в модели парной регрессии − это коэффициент модели регрессии. Значение параметра 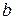характеризует, насколько в среднем изменится зависимая переменная 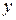при изменении факторной переменной на единицу своего измерения.

Знак коэффициента модели регрессии, в модели парной регрессии указывает на направление связи между изучаемыми переменными.

Если 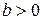, то связь между переменными прямая, т.е. с увеличением переменной увеличивается и переменная 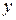и наоборот.

Если коэффициент 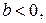то связь между переменными обратная, т.е. с увеличением переменной переменная 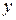уменьшается и наоборот.