Модель информационного управления

С теоретико-игровой точки зрения задача управления состоит в том, чтобы сформировать для управляемых субъектов (агентов) такую игру, чтобы ее исход был наиболее благоприятным для управляющего органа (центра). Соответственно, задачу информационного управления можно неформально (качественно) сформулировать следующим образом: найти такую структуру информированности, чтобы исход рефлексивной игры (см. раздел 6.2) агентов (информационное равновесие) был бы наиболее благоприятен для центра.

Перейдем к формальной постановке задачи. Пусть на множестве действий реальных агентов и структур информированности задана целевая функция центра Ф(x, I). Пусть, далее, центр может сформировать любую структуру информированности из некоторого множества . При структуре информированности вектор действий реальных агентов является элементом множества равновесных векторов 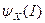. Множество 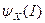может быть пустым, тогда центр, ввиду отсутствия равновесия, не может рассчитывать на тот или иной исход игры. Поэтому введем множество допустимых структур, для которых существует хотя бы одно равновесие: .

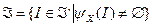Если при заданной структуре множество равновесных векторов 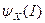состоит более чем из одного элемента, то обычно принимается одно из следующих двух предположений:

1) гипотеза благожелательности (ГБ), состоящая в том, что у центра есть возможность обеспечить выбор агентами «нужного» равновесия;

2) принцип максимального гарантированного результата (МГР), состоящий в том, что центр рассчитывает на наихудшее для себя равновесие игры агентов.

В соответствии с ГБ и МГР получаем, соответственно, постановку задачи информационного управления в двух вариантах:

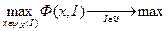; (6.1)

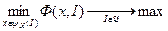. (6.2)

Разумеется, в случае, когда для любого множество 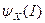состоит ровно из одного элемента, (6.1) и (6.2) совпадают.

Задачу (6.1) (либо (6.2)) будем называть задачей информационного управления в форме целевой функции.

Опишем теперь задачу информационного управления в несколько иной постановке, не зависящей от целевой функции центра. Пусть центр стремится добиться от агентов выбора вектора действий 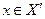. Зададимся вопросом: для каких векторов х и каким образом (то есть при помощи формирования какой структуры I) центр может это сделать? Иначе говоря, вторая возможная постановка задачи информационного управления состоит в нахождении множества достижимости - множества векторов 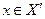, для каждого из которых множество структур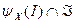

(6.3) непусто,

либо

(6.4) состоит ровно из одного элемента,

а также соответствующих допустимых структур информированности 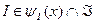для каждого такого вектора х. Условие (6.3) соответствует ГБ, условие (6.4) - МГР.

Задачу (6.3) (либо (6.4)) будем называть задачей информационного управления в форме множества достижимости.

Еще раз подчеркнем, что вторая постановка не зависит от целевой функции центра и отражает лишь его возможность при помощи информационного управления привести систему в то или иное состояние.

Как в первой, так и во второй постановке центр может либо интересоваться, либо не интересоваться стабильностью (см. раздел 6.3) получившегося информационного равновесия. Если требуется осуществить стабильное информационное управление, то есть привести систему в стабильное информационное равновесие, то в приведенных выше постановках требуется заменить 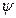на 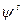, а термины «равновесие» и «равновесный» – на «стабильное равновесие» и «стабильно-равновесный» соответственно.

Моделирование информационного управления. Предлагаемая модель информационного управления представлена на рис. 6.1.

Модель включает в себя агента (агентов) и управляющий орган – центр. Каждый агент характеризуется циклом «информированность агента 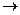действие агента 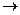наблюдаемый агентом результат 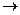информированность агента», и у разных агентов эти три компоненты цикла являются, вообще говоря, различными. В то же время, и это отражает надпись «Агент (ы)» на рис.6.1, можно считать этот цикл общим для всей управляемой подсистемы, то есть для всего набора агентов.

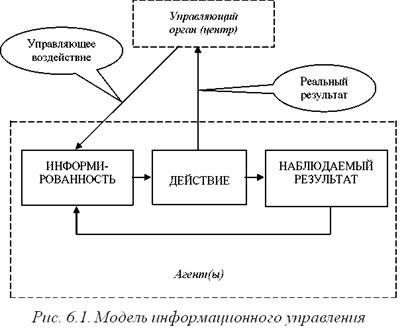
Что касается взаимодействия агента (агентов) и центра, то оно характеризуется:

1) информационным воздействием центра, формирующим ту или иную информированность агента (агентов);

2) реальным результатом действия агента (агентов), который оказывает влияние на интересы центра.

Обсудим модель, изображенную на рис. 6.1, более подробно.

Математическим аппаратом, моделирующим теоретико-игровое взаимодействие агентов, являются рефлексивные игры, в которых агенты выбирают действия на основе своих структур информированности – иерархии представлений о существенных параметрах ситуации («состоянии природы»), представлений о представлениях оппонентов (других агентов) и т.д. Таким образом, в терминах рефлексивных игр информированность агента моделируется при помощи его структуры информированности (соответственно, информированность всей управляемой подсистемы моделируется при помощи структуры информированности игры, являющейся объединением структур информированности агентов).

Исходя из своей структуры информированности, агент выбирает то или иное действие. Для заданной структуры информированности действия агентов являются компонентами информационного равновесия, являющегося решением рефлексивной игры. Информационное равновесие является обобщением равновесия Нэша – наиболее распространенной концепции решения некооперативных игр. Информированность агента о ситуации и о представлениях оппонентов может быть, вообще говоря, неадекватной. Поэтому наблюдаемый агентом результат рефлексивной игры может как соответствовать его ожиданиям, так и не соответствовать им. Соответствие определяется двумя факторами:

1) насколько адекватно информирован агент на момент выбора своего действия;

2) насколько подробную информацию о результатах игры он наблюдает.

Например, наблюдаемым результатом может быть значение его целевой функции, действия оппонентов, истинное значение неопределенного параметра и пр. В общем случае агент наблюдает значение некоторой функции, зависящей от состояния природы и действий оппонентов. Эта функция называется функцией наблюдения, и воздействие ее значения на информированность отображено на рисунке фрагментом «наблюдаемое действие информированность». Если все агенты наблюдают именно тот результат, на какой рассчитывают (то есть реальное значение функции наблюдения каждого агента равно ожидаемому), то естественным является предположение о том, что структура информированности не меняется. В этом случае информационное равновесие является стабильным (см. ниже).

Рассмотрим теперь взаимодействие агентов с центром. Осуществляя информационное управление, центр стремится к максимизации своей полезности (разумеется, это относится и к другим типам управления). Если считать, что центр может сформировать любую структуру информированности из некоторого допустимого множества, то задачу информационного управления можно сформулировать следующим образом: найти такую структуру информированности из допустимого множества структур, чтобы полезность центра в информационном равновесии была максимальной (быть может, с учетом затрат центра на формирование структуры).

Подчеркнем следующее важное обстоятельство: в рамках предлагаемой модели мы исходим из предположения о том, что центр может сформировать у агентов любую структуру информированности. За рамками наших рассмотрений остается вопрос о том, каким образом центру следует «убедить» агентов в том, что имеют место те или иные состояния природы и представления оппонентов.

Можно, однако, в рамках рассматриваемой модели классифицировать способы управляющего воздействия на информированность агентов для формирования той или иной структуры. Такими способами являются:

1) информационное регулирование – целенаправленное влияние на информацию о состоянии природы;

2) рефлексивное управление – целенаправленное влияние на информацию о представлениях оппонентов;

3) активный прогноз – целенаправленное сообщение информации о будущих значениях параметров, зависящих от состояния природы и действий агентов.

Классификация задач информационного управления. В лекции рассматриваются двухуровневые ОС с одним центром и многими агентами в условиях неполной информированности агентов – каждый из субъектов может иметь свои представления о природе.

Задачу информационного управления будем рассматривать:

1) в форме целевой функции либо множества достижимости;

2) с использованием гипотезы благожелательности (ГБ) либо принципа максимально гарантированного результата (МГР);

3) с требованием стабильности или без требования стабильности.

Выбор одного из этих восьми вариантов определяется конкретной моделируемой ситуацией. Однако в любом случае необходимым (и, как показывает опыт, наиболее сложным и трудоемким для исследователя) этапом является установление связи между структурой информированности и вектором действий агентов, то есть исследование информационного равновесия.