2014-02-02
1093
Рассмотрим организационную систему, состоящую из центра и одного агента. Центр продает агенту некий товар в количестве q за сумму t. Функция полезности центра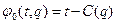 
. Функция C (q) – стоимость производства товара для центра – дважды дифференцируемая выпуклая функция, C’ (0)=0, C’ (∞)=∞. Функция полезности агента 
. 
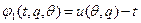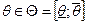– положительный параметр, тип агента. Функция 
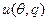– полезность товара для агента – возрастает и вогнута по q и возрастает по 
.
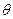Центру известно множество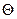 
и вероятностное распределение типа агента на этом множестве, причем интегральная функция распределения 
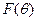дифференцируема - 
.
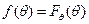Задача центра - максимизировать свою ожидаемую полезность:
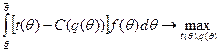
На основании принципа выявления строится неманипулируемый механизм - «меню» контрактов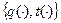 
, зависящий от сообщаемой агентом оценки своего типа. (Принцип выявления – западный аналог принципа открытого управления (см. выше). Для систем с одним агентом эти принципы эквивалентны).
Необходимые условия неманипулируемости механизма имеют следующий вид:
|
|
|
При выполнении условий Спенса-Мирлиса:
,
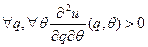доказано, что функция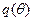 
является неубывающей функцией своего аргумента.
Предполагается, что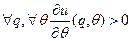 
. Вводится функция прибыли агента при использовании оптимального неманипулируемого механизма в зависимости от его типа - 
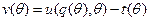.Причем, при выполнении условия IC 1, 
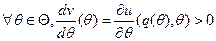. Поэтому, выполнение условий индивидуальной рациональности агента 
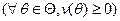может быть обеспечено следующим образом 
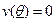, из чего следует, что: 
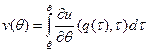, и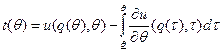 
.
Задача центра (построение механизма, максимизирующего его прибыль) сводится к решению следующего уравнения:
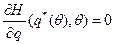
при условии
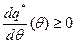б (5.3)
где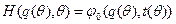 
.
Возможны два случая: ограничение (5.3) выполняется всюду как строгое неравенство или при некоторых 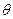ограничение (5.3) выполняется как равенство.
Первый случай очень прост: множитель Лагранжа при ограничении (5.3) равен нулю и 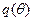определяется из условия 
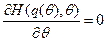, то есть:
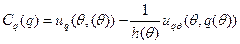, (5.4.)
где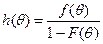 
.
Каждый тип агентов получает свой контракт (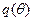строго возрастает по 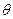). Таким образом, все типы, кроме самого высокого, получают уровень q меньше оптимального, а самый высокий тип получает эффективное количество.
Если же хотя бы при некоторых 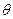в ограничение (5.3) выполняется как равенство, ситуация гораздо сложнее. Для решения задачи нужно использовать принцип максимума Понтрягина. Рассмотрим динамическую задачу максимизации:
,
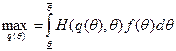где θ - аналог времени, q - фазовая переменная, изменяющаяся по закону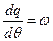 
, а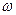 
– управление, ограниченное снизу: 
.
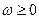Как правило, задачу решают следующим образом. Сначала предполагают, что контракт разделяющий, и вычисляют 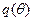из (5.4). Если полученная функция 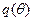не убывает, то задача решена, оптимальный контракт разделяющий. Если же полученная функция имеет убывающие участки, но необходимо решать изложенную выше задачу оптимального управления. При этом некоторые агенты с различными типами получат одинаковые контракты, то есть равновесие частично смешивающее.
|
|
|
Пример 5.4. Пусть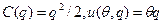 
,а тип агента распределен равномерно на множестве допустимых значений -
.
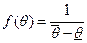Тогда получаем, что
,
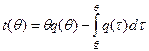а 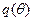определяется из решения уравнения 5.4:
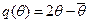
С учетом требований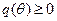 
- покупателю может продаваться лишь положительное количество товара получаем следующее меню контрактов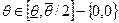: для 
, для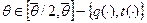 
:
,
где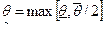 
.
Итак, стандартная модель теории контрактов, рассмотренная выше, может быть применена для формирования гибкой шкалы цен на товар производителя - монополиста. Выставляя на продажу различные модификации своей продукции по различным ценам (что и является тем самым «меню» контрактов) производитель охватывает различные группы пользователей. Классический пример такого товара - вино. Чем дольше срок его выдержки, тем выше качество вина. Ценители вина готовы покупать более качественное вино по более высокой цене, неискушенные потребители готовы довольствоваться менее качественным продуктом по более низкой цене.
Используя модель теории контрактов, производитель может оптимизировать свой ожидаемый доход от продажи своего товара.
Но, варьироваться может не только качество товара, но и его объем. Чем большее количество товара приобретает покупатель, тем ниже его удельная стоимость. Зависимость цены товара от приобретаемого количества и является тем самым меню контрактов, которое может быть получено с помощью стандартной модели теории контрактов. Основной проблемой, возникающей при решении практических задач, является идентификация понятия типа покупателя и возможных пределов его значений.
