Рефлексивные игры

Рассмотрим множество N= {1, 2, …, n } агентов. Если в ситуации присутствует неопределенный параметр 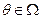(будем считать, что множество 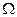является общим знанием), то структура информированности I_i (как синоним будем употреблять термины информационная структура и иерархия представлений) i -го агента включает в себя следующие элементы. Во-первых, представление i -го агента о параметре 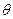– обозначим его 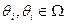. Во-вторых, представления i -го агента о представлениях других агентов о параметре 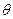– обозначим их 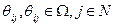. В-третьих, представления i -го агента о представлении j -го агента о представлении k- го агента – обозначим их 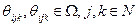. И так далее.

Таким образом, структура информированности I_i i -го агента задается набором всевозможных значений вида 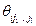, где l пробегает множество целых неотрицательных чисел, 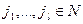, а .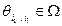

Аналогично задается структура информированности I игры в целом – набором значений 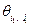, где l пробегает множество целых неотрицательных чисел, 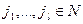, а 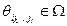. Подчеркнем, что структура информированности I «недоступна» наблюдению агентов, каждому из которых известна лишь некоторая ее часть (а именно – I_i).

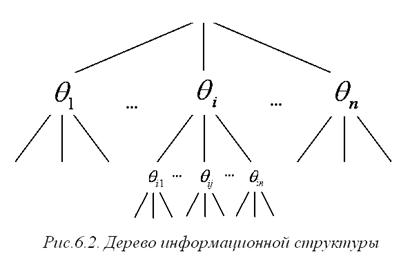
Таким образом, структура информированности - бесконечное n- дерево (то есть тип структуры постоянен и является n -деревом), вершинам которого соответствует конкретная информированность реальных и фантомных агентов.

Рефлексивной игрой Г_I называется игра, описываемая следующим кортежем:

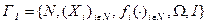, (6.5)

где N - множество реальных агентов, X_i - множество допустимых действий i -го агента, 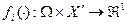- его целевая функция, 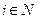, 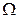- множество возможных значений неопределенного параметра, I - структура информированности.

Таким образом, рефлексивная игра является обобщением понятия игры в нормальной форме, задаваемой кортежем 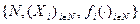, на случай, когда информированность агентов отражена иерархией их представлений (информационной структурой I). В рамках принятого определения «классическая» игра в нормальной форме является частным случаем рефлексивной игры - игры с общим знанием. В «предельном» случае - когда состояние природы является общим знанием - предлагаемая в настоящей работе концепция решения рефлексивной игры (информационное равновесие - см. ниже) переходит в равновесие Нэша.

Совокупность связей между элементами информированности агентов можно изобразить в виде дерева (см. рис. 6.2). При этом структура информированности i -го агента изображается поддеревом, исходящим из вершины .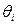

Сделаем важное замечание: в данной лекции мы ограничимся рассмотрением «точечной» структуры информированности, компоненты которой состоят лишь из элементов множества 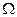. (Более общим случаем является, например, интервальная или вероятностная информированность.)

Стратегическая и информационная рефлексия. Итак, рефлексивной является игра, в которой информированность игроков не является общим знанием. С точки зрения теории игр и рефлексивных моделей принятия решений целесообразно разделять стратегическую и информационную рефлексию.

Информационная рефлексия – процесс и результат размышлений игрока о том, каковы значения неопределенных параметров, что об этих значениях знают и думают его оппоненты (другие игроки). При этом собственно «игровая» компонента отсутствует, так как никаких решений игрок не принимает.

Иными словами, информационная рефлексия относится к информированности агента о природной реальности (какова игра), и о рефлексивной реальности (какой видят игру другие). Информационная рефлексия логически предшествует рефлексии несколько иного рода – стратегической рефлексии.

Стратегическая рефлексия – процесс и результат размышлений игрока о том, какие принципы принятия решений используют его оппоненты (другие игроки) в рамках той информированности, которую он им приписывает в результате информационной рефлексии. Таким образом, информационная рефлексия имеет место только в условиях неполной информированности, и ее результат используется при принятии решений (в том числе – при стратегической рефлексии). Стратегическая рефлексия имеет место даже в случае полной информированности, предваряя принятие игроком решения о выборе действия (стратегии). Другими словами, информационная и стратегическая рефлексии могут изучаться независимо, однако в условиях неполной информированности обе они имеют место.

Далее для формулировки некоторых определений и свойств нам понадобятся следующие обозначения:

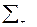– множество всевозможных конечных последовательностей индексов из N;

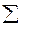– объединение 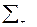с пустой последовательностью;

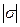– количество индексов в последовательности 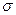(для пустой последовательности принимается равным нулю), которое выше было названо длиной последовательности индексов.

Если 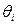- представления i -го агента о неопределенном параметре, а 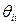- представления i -го агента о собственном представлении, то естественно считать, что 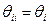. Иными словами, i -й агент правильно информирован о собственных представлениях, а также считает, что таковы и другие агенты и т.д. Формально это означает, что выполнена аксиома автоинформированности, которую далее будем предполагать выполненной:

.

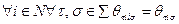Эта аксиома означает, в частности, что, зная 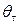для всех 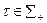таких, что 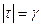, можно однозначно найти 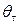для всех 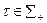таких, что .

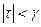Наряду со структурами информированности I_i, 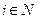, можно рассматривать структуры информированности I_ij (структура информированности j -го агента в представлении i -го агента), I_ijk и т.д. Отождествляя структуру информированности с характеризуемым ею агентом, можно сказать, что, наряду с n реальными агентами (i-агентами, где 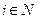)со структурами информированности I_i, в игре участвуют фантомные агенты ( 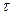-агенты, где 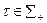, 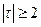) со структурами информированности 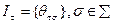. Фантомные агенты, существуя в сознании реальных агентов, влияют на их действия, о чем пойдет речь далее.

Определим фундаментальное для дальнейших рассмотрений понятие тождественности структур информированности.

Структуры информированност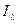и и 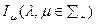называются тождественными если выполнены два условия

1) 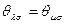для любого ;

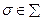2) последние индексы в последовательностях 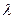и 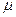совпадают.

Будем обозначать тождественность структур информированности следующим образом: .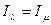

Первое из двух условий в определении тождественности структур прозрачно, второе же требует некоторых пояснений. Дело в том, что далее мы будем обсуждать действие 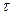-агента в зависимости от его структуры информированности 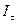и целевой функции f_i, которая как раз определяется последним индексом последовательности 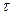. Поэтому удобно считать, что тождественность структур информированности означает в том числе и тождественность целевых функций.

Назовем 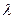-агента 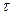-субъективно адекватно информированным о представлениях 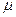-агента (или, короче, о 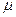-агенте), если

.

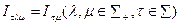Будем обозначать 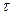-субъективную адекватную информированность 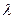-агента о 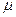-агенте следующим образом: .

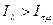Понятие тождественности структур информированности позволяет определить их важное свойство – сложность. Заметим, что наряду со структурой I имеется счетное множество структур 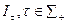, среди которых можно при помощи отношения тождественности выделить классы попарно нетождественных структур. Количество этих классов естественно считать сложностью структуры информированности.

Будем говорить, что структура информированности I имеет конечную сложность v=v(I), если существует такой конечный набор попарно нетождественных структур 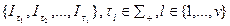, что для любой структуры 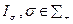, найдется тождественная ей структура 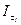из этого набора. Если такого конечного набора не существует, будем говорить, что структура I имеет бесконечную сложность: .

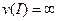Структуру информированности, имеющую конечную сложность, будем называть конечной (еще раз отметим, что при этом дерево структуры информированности все равно остается бесконечным). В противном случае структуру информированности будем называть бесконечной.

Ясно, что минимально возможная сложность структуры информированности в точности равна числу участвующих в игре реальных агентов (напомним, что по определению тождественности структур информированности они попарно различаются у реальных агентов).

Любой набор (конечный или счетный) попарно нетождественных структур 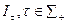, такой, что любая структура 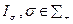, тождественна одной из них, называется базисом структуры информированности I.

Если структура информированности I имеет конечную сложность, то можно определить максимальную длину последовательности индексов 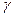такую, что, зная все структуры 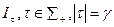, можно найти и все остальные структуры. Эта длина в определенном смысле характеризует ранг рефлексии, необходимый для описания структуры информированности.

Будем говорить, что структура информированности I, 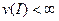, имеет конечную глубину 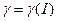, если:

1) для любой структуры 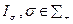, найдется тождественная ей структура ;

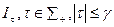2) для любого целого положительного числа 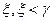, существует структура 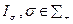, не тождественная никакой из структур .

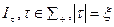Если 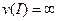, то и глубину будем считать бесконечной: .

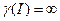Понятия сложности и глубины структуры информированности игры можно рассматривать 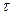-субъективно. В частности, глубину структуры информированности игры с точки зрения 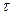-агента, 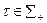, будем называть рангом рефлексии 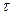-агента.

Граф рефлексивной игры. Если структура информированности имеет конечную сложность, то можно построить граф рефлексивной игры, наглядно показывающий взаимосвязь между действиями агентов (как реальных, так и фантомных), участвующих в равновесии.

Вершинами этого ориентированного графа являются действия 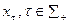, отвечающие попарно нетождественным структурам информированности 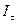, или компоненты структуры информированности 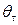, или просто номер 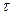реального или фантомного агента, .

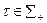Между вершинами проведены дуги по следующему правилу: к каждой вершине 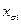проведены дуги от (n –1) вершин, отвечающих структурам 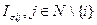. Если две вершины соединены двумя противоположно направленными дугами, будем изображать одно ребро с двумя стрелками.

Подчеркнем, что граф рефлексивной игры соответствует системе уравнений (6.6) (то есть определению информационного равновесия), в то время как решения ее может и не существовать.

Итак, граф G_I рефлексивной игры Г_I (см. определение рефлексивной игры выше), структура информированности которой имеет конечную сложность, определяется следующим образом:

1) вершины графа G_I соответствуют реальным и фантомным агентам, участвующим в рефлексивной игре, то есть попарно нетождественным структурам информированности;

2) дуги графа G_I отражают взаимную информированность агентов: если от одного агента (реального или фантомного) существует путь к другому агенту, то второй адекватно информирован о первом.

Если в вершинах графа G_I изображать представления соответствующего агента о состоянии природы, то рефлексивная игра Г_I с конечной структурой информированности I может быть задана кортежем 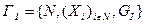, где N - множество реальных агентов, X_i - множество допустимых действий i -го агента, 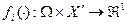- его целевая функция, 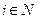, G_I - граф рефлексивной игры.

Отметим, что во многих случаях рефлексивную игру более удобно (и наглядно) описывать именно в терминах графа G_I, а не дерева информационной структуры (см. ниже примеры графов рефлексивных игр).