Если задана структура I информированности игры, то тем самым задана и структура информированности каждого из агентов (как реальных, так и фантомных). Выбор 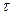 - агентом своего действия
- агентом своего действия 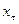 в рамках гипотезы рационального поведения определяется его структурой информированности
в рамках гипотезы рационального поведения определяется его структурой информированности 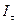 , поэтому, имея перед собой эту структуру, можно смоделировать его рассуждения и определить это его действие. Выбирая свое действие, агент моделирует действия других агентов (осуществляет рефлексию). Поэтому при определении исхода игры необходимо учитывать действия как реальных, так и фантомных агентов.
, поэтому, имея перед собой эту структуру, можно смоделировать его рассуждения и определить это его действие. Выбирая свое действие, агент моделирует действия других агентов (осуществляет рефлексию). Поэтому при определении исхода игры необходимо учитывать действия как реальных, так и фантомных агентов.
Набор действий 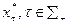 , называется информационным равновесием, если выполнены следующие условия:
, называется информационным равновесием, если выполнены следующие условия:
1) структура информированности I имеет конечную сложность v; (6.6)
2) 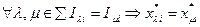 ;
;
3) 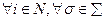
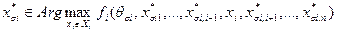 .
.
Первое условие в определении информационного равновесия означает, что в рефлексивной игре участвует конечное число реальных и фантомных агентов.
Второе условие отражает требование того, что одинаково информированные агенты выбирают одинаковые действия.
И, наконец, третье условие отражает рациональное поведение агентов - каждый из них стремится выбором собственного действия максимизировать свою целевую функцию, подставляя в нее действия других агентов, которые оказываются рациональными с точки зрения рассматриваемого агента в рамках имеющихся у него представлений о других агентах.
В соответствии с условием 2, для определения информационного равновесия требуется решить, казалось бы, бесконечное (счетное) число уравнений и получить столько же значений 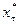 . Однако оказывается, что на самом деле число уравнений и значений конечно.
. Однако оказывается, что на самом деле число уравнений и значений конечно.
Утверждение 6.1. Если информационное равновесие 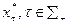 , существует, то оно состоит из не более чем v попарно различных действий, а в системе (6.6) содержится не более чем v попарно различных уравнений.
, существует, то оно состоит из не более чем v попарно различных действий, а в системе (6.6) содержится не более чем v попарно различных уравнений.
Доказательство. Пусть 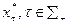 , - информационное равновесие. Тогда из конечности структуры информированности и условия 2 сразу следует, что попарно различных чисел
, - информационное равновесие. Тогда из конечности структуры информированности и условия 2 сразу следует, что попарно различных чисел 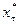 не более v.
не более v.
Рассмотрим две любые тождественные структуры информированности: 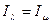 . Соответственно, имеем
. Соответственно, имеем 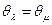 , и
, и 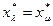 . Далее, для любого
. Далее, для любого 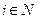 справедливо
справедливо  , следовательно,
, следовательно, 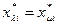 . Поэтому два уравнения системы (6.6), у которых в левой части стоят действия
. Поэтому два уравнения системы (6.6), у которых в левой части стоят действия 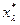 и
и 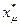 , тождественно совпадают. Так как имеется v попарно различных структур информированности, количество попарно различных условий (6.6) не превышает v.
, тождественно совпадают. Так как имеется v попарно различных структур информированности, количество попарно различных условий (6.6) не превышает v. 
Таким образом, для нахождения информационного равновесия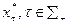 , достаточно записать v условий (6.6) для каждого из v попарно различных значений
, достаточно записать v условий (6.6) для каждого из v попарно различных значений 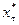 , отвечающих попарно различным структурам информированности
, отвечающих попарно различным структурам информированности 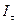 .
.
Если все агенты являются одинаково информированными, то сложность структуры информированности минимальна и равна числу агентов. В этом случае система (6.6) переходит в определение равновесия Нэша, а информационное равновесие - в равновесие Нэша.
Итак, в случае, когда все реальные агенты являются одинаково информированными (то есть рефлексивная реальность является общим знанием), информационное равновесие переходит в равновесие Нэша (фантомных агентов «не возникает»).
Информационное равновесие (см. (6.6)) является достаточно громоздкой конструкцией, и сразу увидеть связь между информационной структурой и информационным равновесием зачастую бывает затруднительно. Удобным языком описания взаимной информированности агентов и выразительным средством анализа свойств информационного равновесия является граф рефлексивной игры, описанный выше.
Рассмотрим несколько примеров нахождения информационного равновесия с помощью графа рефлексивной игры.
Примеры 6.1, 6.2. В этих примерах участвуют три агента с целевыми функциями следующего вида:
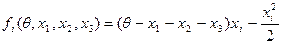 ,
,
где 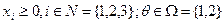 .
.
Содержательно, xi - объем выпуска продукции i -м агентом, 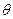 - спрос на производимую продукцию. Тогда первое слагаемое в целевой функции может интерпретироваться как произведение цены на объем продаж - выручка от продаж, а второе слагаемое - как затраты на производство.
- спрос на производимую продукцию. Тогда первое слагаемое в целевой функции может интерпретироваться как произведение цены на объем продаж - выручка от продаж, а второе слагаемое - как затраты на производство.
Для краткости будем называть агента, считающего, что спрос низкий 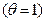 , пессимистом, а считающего, что спрос высокий
, пессимистом, а считающего, что спрос высокий 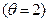 - оптимистом. Таким образом, в примерах 6.1, 6.2 ситуации различаются лишь вследствие различных структур информированности.
- оптимистом. Таким образом, в примерах 6.1, 6.2 ситуации различаются лишь вследствие различных структур информированности.
Пример 6.1. Пусть первые два агента оптимисты, а третий - пессимист, причем все трое одинаково информированы.
В соответствии со свойством 2 определения информационного равновесия, аналогичные соотношения выполняются для равновесных действий 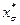 .
.
Видно, что любая структура информированности тождественна одной из трех, образующих базис: { I 1, I 2, I 3}. Поэтому сложность данной структуры информированности равна трем, а глубина равна единице. Граф рефлексивной игры изображен на рис. 6.3.
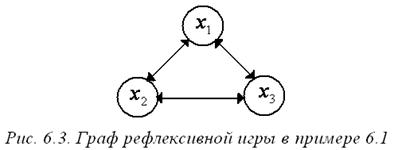
Для нахождения информационного равновесия надо решить следующую систему уравнений (см. (6.6)):
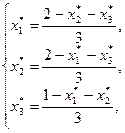
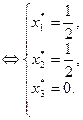
Таким образом, действия агентов в ситуации информационного равновесия будут следующими:
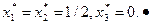
Пример 6.2. Пусть первые два агента оптимисты, а третий – пессимист, который считает всех трех агентов одинаково информированными пессимистами. Первые два агента одинаково информированы, причем оба они адекватно информированы о третьем агенте.
Сложность данной структуры информированности равна пяти, а глубина равна двум. Граф рефлексивной игры изображен на рис. 6.4.
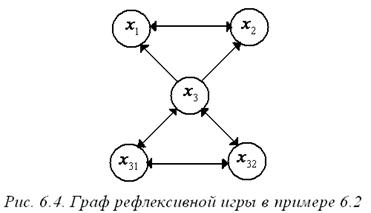
Для нахождения информационного равновесия надо решить следующую систему уравнений (см. (6.6)):
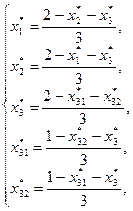
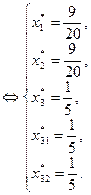
Таким образом, действия реальных агентов в ситуации информационного равновесия будут следующими: 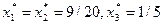 .
.
Отметим, что лишь изменением информированности (переходом от информационной структуры рис. 6.3 к структуре рис. 6.4) удалось увеличить как суммарный объем выпускаемой агентами продукции, так и их суммарный выигрыш.
Стабильное информационное равновесие. Одной из особенностей «классического» равновесия Нэша является его самоподдерживающийся характер – если игра повторяется несколько раз и все игроки, кроме i -го, выбирают одни и те же равновесные действия, то и i -му нет резона отклоняться от своего равновесного действия. Это обстоятельство очевидным образом связано с тем, что представления всех игроков о реальности адекватны – значение состояния природы является общим знанием.
В случае информационного равновесия ситуация, вообще говоря, может быть иной. Действительно, в результате однократного разыгрывания игры может оказаться, что какие-то из игроков (или даже все) наблюдают не тот результат, на который они рассчитывали. Это может быть связано как с неверным представлением о состоянии природы, так и с неадекватной информированностью о представлениях оппонентов. В любом случае, самоподдерживающийся характер равновесия нарушается – если игра повторяется, действия игроков могут измениться.
Однако в некоторых случаях самоподдерживающийся характер равновесия может иметь место и при различных (и, вообще говоря, неверных) представлениях агентов. Говоря неформально, это происходит тогда, когда каждый агент (как реальный, так и фантомный) наблюдает тот результат игры, которого ожидает. Для формального изложения нам понадобится дополнить описание рефлексивной игры.
Напомним, что рефлексивная игра задается кортежем 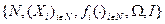 , где N= {1,2, …, n } - множество участников игры (игроков, агентов), Xi - множество допустимых действий i -го агента,
, где N= {1,2, …, n } - множество участников игры (игроков, агентов), Xi - множество допустимых действий i -го агента, 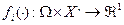 - его целевая функция,
- его целевая функция, 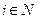 , I - структура информированности. Дополним эту конструкцию набором функций
, I - структура информированности. Дополним эту конструкцию набором функций 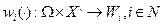 , каждая из которых отображает вектор
, каждая из которых отображает вектор 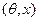 в элемент wi некоторого множества Wi. Этот элемент wi и есть то, что i -й агент наблюдает в результате разыгрывания игры.
в элемент wi некоторого множества Wi. Этот элемент wi и есть то, что i -й агент наблюдает в результате разыгрывания игры.
Функцию 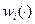 будем называть функцией наблюдения i -го агента. Будем считать, что функции наблюдения являются общим знанием среди агентов.
будем называть функцией наблюдения i -го агента. Будем считать, что функции наблюдения являются общим знанием среди агентов.
Если 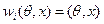 , то есть
, то есть 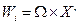 , то i -й агент наблюдает как состояние природы, так и действия всех агентов. Если, напротив, множество Wi состоит из одного элемента, то i -й агент ничего не наблюдает.
, то i -й агент наблюдает как состояние природы, так и действия всех агентов. Если, напротив, множество Wi состоит из одного элемента, то i -й агент ничего не наблюдает.
Пусть в рефлексивной игре существует информационное равновесие 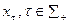 (напомним, что
(напомним, что 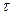 - произвольная непустая конечная последовательность индексов из N). Зафиксируем
- произвольная непустая конечная последовательность индексов из N). Зафиксируем 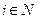 и рассмотрим i -го агента. Он ожидает в результате игры пронаблюдать величину:
и рассмотрим i -го агента. Он ожидает в результате игры пронаблюдать величину:
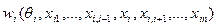 . (6.7)
. (6.7)
На самом же деле он наблюдает величину:
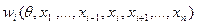 (6.8)
(6.8)
Поэтому требование стабильности для i -агента означает совпадение величин (6.7) и (6.8) (напомним, что эти величины являются элементами некоторого множества Wi).
Пусть величины (6.7) и (6.8) равны, то есть i -агент и после разыгрывания игры не сомневается в истинности своих представлений. Однако является ли это достаточным основанием для того, чтобы он и в следующий раз выбрал то же действие xi? Ясно, что ответ отрицательный, что продемонстрируем на следующем примере.
Пример 6.3. Пусть в рефлексивной биматричной игре, где 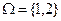 , выигрыши заданы биматрицами (агент 1 выбирает строку, агент 2 - столбец, то есть Х1 = Х2 ={1;2}), приведенными на рис. 6.5,
, выигрыши заданы биматрицами (агент 1 выбирает строку, агент 2 - столбец, то есть Х1 = Х2 ={1;2}), приведенными на рис. 6.5,
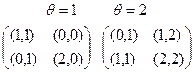
Рис. 6.5. Матрицы выигрышей в примере 6.3
а граф рефлексивной игры имеет вид, изображенный на рис. 6.6.
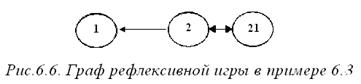
Пусть при этом 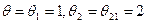 , и каждый агент наблюдает свой выигрыш (то есть функция наблюдения агента совпадает с его функцией выигрыша). Ясно, что информационным равновесием является набор х1 = х2 = х21 =2, то есть первый и второй агенты, а также 21-агент и все прочие фантомные агенты выбирают вторые действия. Однако реальное состояние природы
, и каждый агент наблюдает свой выигрыш (то есть функция наблюдения агента совпадает с его функцией выигрыша). Ясно, что информационным равновесием является набор х1 = х2 = х21 =2, то есть первый и второй агенты, а также 21-агент и все прочие фантомные агенты выбирают вторые действия. Однако реальное состояние природы 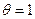 становится известным второму агенту после розыгрыша игры (и получения им выигрыша 0 вместо ожидаемого 2). Поэтому в следующий раз второй агент выберет действие х2 =1, что побуждает и первого агента изменить свое действие (выбрать х 1 =1).
становится известным второму агенту после розыгрыша игры (и получения им выигрыша 0 вместо ожидаемого 2). Поэтому в следующий раз второй агент выберет действие х2 =1, что побуждает и первого агента изменить свое действие (выбрать х 1 =1).
Таким образом, для стабильности равновесия необходимо чтобы и ij -агент, 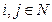 , наблюдал «нужную» величину. Он ожидает в результате игры пронаблюдать:
, наблюдал «нужную» величину. Он ожидает в результате игры пронаблюдать:
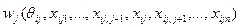 . (6.9)
. (6.9)
На самом же деле (то есть i -субъективно, ведь ij -агент существует в сознании i -агента) он наблюдает величину:
 . (6.10)
. (6.10)
Поэтому требование стабильности для ij -агента означает совпадение величин (6.9) и (6.10).
В общем случае, то есть для 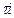 -агента,
-агента, 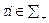 , условие стабильности определим следующим образом.
, условие стабильности определим следующим образом.
Информационное равновесие 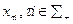 , будем называть стабильным при заданной структуре информированности I, если для любого
, будем называть стабильным при заданной структуре информированности I, если для любого 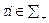 выполняется
выполняется
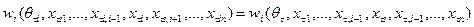 . (6.11)
. (6.11)
Информационное равновесие, не являющееся стабильным, будем называть нестабильным. В частности, информационное равновесие в примере 6.3 является нестабильным.
Утверждение 6.2. Пусть структура информированности I имеет сложность v и существует информационное равновесие 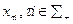 . Тогда система соотношений (6.11) содержит не более чем v попарно различных условий.
. Тогда система соотношений (6.11) содержит не более чем v попарно различных условий.
Доказательство. Рассмотрим две любые тождественные структуры информированности: 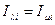 . Поскольку
. Поскольку 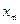 - равновесие, имеем
- равновесие, имеем 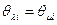 ,
, 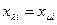 ,
, 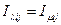 ,
, 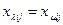 для любого
для любого 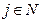 . Поэтому условия стабильности (6.11) для
. Поэтому условия стабильности (6.11) для 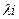 - и
- и 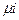 -агентов тождественно совпадают. Так как имеется v попарно различных структур информированности, количество попарно различных условий (6.11) не превышает v.
-агентов тождественно совпадают. Так как имеется v попарно различных структур информированности, количество попарно различных условий (6.11) не превышает v. 
Истинное и ложное информационные равновесия. Стабильные информационные равновесия будем разделять на два класса - истинные и ложные равновесия. Определение предварим примером.
Пример 6.4. Рассмотрим игру, в которой участвуют три агента с целевыми функциями:
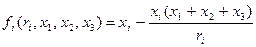 ,
,
где 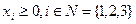 . Целевые функции являются общим знанием с точностью до типов агентов - параметров ri >0. Вектор r=(r 1, r 2, r 3) типов агентов может интерпретироваться как состояние природы. При этом здесь и далее подразумевается, что свой собственный тип известен каждому агенту достоверно.
. Целевые функции являются общим знанием с точностью до типов агентов - параметров ri >0. Вектор r=(r 1, r 2, r 3) типов агентов может интерпретироваться как состояние природы. При этом здесь и далее подразумевается, что свой собственный тип известен каждому агенту достоверно.
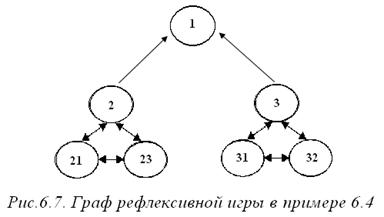
Граф рефлексивной игры имеет вид, изображенный на рис. 6.7, при этом r 2= r 3= r, r 21= r 23= r 31= r 32 =c. Общим знанием является следующее: каждый игрок знает свой тип и наблюдает сумму действий оппонентов.
Нетрудно вычислить единственное информационное равновесие этой игры:
x 2 =x 3=(3 r -2 c)/4, (6.12)
x 21= x 23= x 31= x 32=(2 c - r)/4,
x 1=(2 r 1-3 r +2 с)/4.
Условия стабильности (см. (6.11)) в данном случае выглядят следующим образом:
x 21+ x 23= x 1+ x 3, x 31+ x 32= x 1+x2. (6.13)
Записаны условия для 2- и 3-агентов, поскольку для 1-, 21-, 23-, 31-, 32-агентов они тривиальны.
Подставляя (6.12) в (6.13), получаем, что необходимым и достаточным условием стабильности является равенство:
2 c = r 1+ r. (6.14)
Пусть условие (6.14) выполнено. Тогда равновесные действия реальных агентов таковы:
x 2= x 3=(3 r – r 1)/4, x 1=(3 r 1–2 r)/4. (6.15)
Предположим теперь, что типы агентов стали общим знанием (см. рис. 6.8).
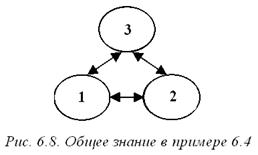
Нетрудно убедиться, что в случае общего знания единственным равновесием будет (6.15).
Таким образом, при выполнении условия (6.14) имеет место несколько парадоксальная ситуация. Представления второго и третьего агентов не соответствуют действительности (рис. 6.7), однако их равновесные действия (6.15) в точности такие, как были бы в случае одинаковой информированности (рис. 5.8). Назовем такое стабильное информационное равновесие истинным.
Пусть набор действий 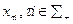 , является стабильным информационным равновесием. Будем называть его истинным равновесием, если набор (x 1, …, xn) является равновесием в условиях общего знания о состоянии природы
, является стабильным информационным равновесием. Будем называть его истинным равновесием, если набор (x 1, …, xn) является равновесием в условиях общего знания о состоянии природы 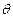 (или о наборе (r 1, …, rn) типов агентов).
(или о наборе (r 1, …, rn) типов агентов).
Из определения, в частности, следует, что в условиях общего знания любое информационное равновесие является истинным. Рассмотрим еще один случай, когда этот факт имеет место.
Утверждение 6.3. Пусть целевые функции агентов имеют вид:
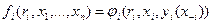 ,
,
а функции наблюдения - вид 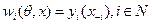 . Содержательно это означает следующее: выигрыш каждого агента зависит от его типа, его действия и функции наблюдения, зависящей от действий остальных агентов (но не от их типов). Тогда любое стабильное равновесие является истинным.
. Содержательно это означает следующее: выигрыш каждого агента зависит от его типа, его действия и функции наблюдения, зависящей от действий остальных агентов (но не от их типов). Тогда любое стабильное равновесие является истинным.
Доказательство. Пусть 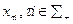 , - стабильное информационное равновесие, и условия утверждения выполнены. Тогда для любого
, - стабильное информационное равновесие, и условия утверждения выполнены. Тогда для любого 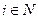 имеем:
имеем:
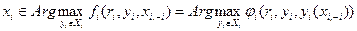 .
.
В силу стабильности справедливо равенство:
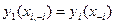 ,
,
поэтому:
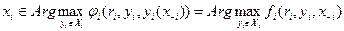 .
.
Последнее соотношение означает (в силу произвольности 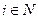 ), что набор (x 1, …, xn) является равновесным при полной информированности.
), что набор (x 1, …, xn) является равновесным при полной информированности.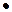
Стабильное информационное равновесие, не являющееся истинным, называется ложным.
Таким образом, ложное равновесие - это такое стабильное информационное равновесие, которое не является равновесием в случае одинаковой информированности агентов (в условиях общего знания).
Пример 6.5. Пусть в рефлексивной биматричной игре, где 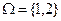 , выигрыши заданы биматрицами (агент 1 выбирает строку, агент 2 - столбец, то есть X1=X2 ={1;2}) на рис. 6.9.
, выигрыши заданы биматрицами (агент 1 выбирает строку, агент 2 - столбец, то есть X1=X2 ={1;2}) на рис. 6.9.
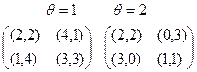
Рис. 6.9. Матрицы выигрышей в примере 6.5
Пусть, далее, в реальности 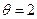 , однако оба агента считают общим знанием
, однако оба агента считают общим знанием 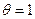 . Каждый агент наблюдает пару (x 1, x 2), которая и является функцией наблюдения.
. Каждый агент наблюдает пару (x 1, x 2), которая и является функцией наблюдения.
Информационным равновесием является выбор каждым агентом действия 1. Если бы общим знанием было бы реальное состояние природы, равновесным был бы выбор каждым агентом действия 2. Таким образом, выигрыши агентов в информационном равновесии оказываются бóльшими, чем если бы общим знанием было реальное состояние природы .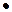
Информационные воздействия. В данном пункте выделены некоторые способы осуществления центром информационного воздействия на агентов с целью формирования той или иной структуры информированности. Эти способы - информационное регулирование, рефлексивное управления, активный прогноз.
Таким образом, в контексте описанной ранее модели информационного управления данный пункт соответствует цепи «центр 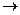 информированность агента (агентов)» (см. рис. 6.1). Отдавая себе отчет в тех ограничениях, которые присущи математическому моделированию человеческого поведения (и, в частности, теоретико-игровому подходу к информационному управлению), рассмотрим возможные виды информационных воздействий.
информированность агента (агентов)» (см. рис. 6.1). Отдавая себе отчет в тех ограничениях, которые присущи математическому моделированию человеческого поведения (и, в частности, теоретико-игровому подходу к информационному управлению), рассмотрим возможные виды информационных воздействий.
Существует следующая классификация информационных воздействий:
1) входные данные - «сухие» факты;
2) входные данные - логически обоснованные выводы, аналитические суждения, опирающиеся на определенный набор фактов;
3) входные данные - эмоционально окрашенные утверждения, опирающиеся на «хорошо/плохо», «морально/аморально», «нравственно/безнравственно» и т. п.
Новая информация, на основании которой агенты принимают решения, делится на:
4) жесткую, содержащую только реальные данные и факты;
5) мягкую, которая включает прогнозы и оценки.
Очевидна аналогия между пунктами (1) и (4), а также (2) и (5). О них речь пойдет несколько ниже, а сейчас остановимся подробнее на пункте (3).
В пункте (3) речь идет, по сути дела, об этическом аспекте информации и, соответственно, об этическом аспекте тех или иных решений. По-видимому, единственной пока попыткой формального описания этого аспекта являются работы В.А Лефевра, а также других авторов, развивающих предложенную им модель этического выбора. В этих работах предполагается, что принимающий решение агент осуществляет рефлексию первого рода, то есть занимает позицию наблюдателя по отношению к своему поведению, своим мыслям и чувствам. В агенте существует несколько соотнесенных друг с другом уровней, в частности, уровень, «отвечающий» за этический аспект выбора. Итоговое решение агента определяется как влиянием внешней среды, так и состоянием этих уровней.
В теории игр (а также и в данной работе) агент понимается как индивид, то есть «неделимый», и осуществляет рефлексию второго рода – относительно принятия решений оппонентами. Поэтому, оставив пункт (3) за рамками наших рассмотрений, обратимся к пунктам (1), (4) и (2), (5).
Структура информированности i -го агента (см. выше) включает в себя представления:
1) о состоянии природы 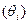 ;
;
2) о представлениях оппонентов 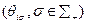 .
.
Сообщение как первого, так и второго может быть элементом информационного воздействия. Иными словами, центр может сообщить агенту (агентам) информацию как о состоянии природы (то есть о значении неопределенного параметра), так и о представлениях оппонентов.
Соответственно, получаем следующие виды информационных воздействий:
(I) информационное регулирование;
(II) рефлексивное управление.
Они примерно соответствуют пунктам (1), (4).
Что касается пунктов (2), (5), то им примерно соответствует такой вид информационного воздействия, как
(III) активный прогноз, представляющий собой сообщение информации о будущих значениях неких параметров, зависящих от состояния природы и действий агентов.
 2014-02-02
2014-02-02 1257
1257
