Механизмы экспертизы

Экспертиза – выявление свойств объекта, процесса, явления путем опроса экспертов. Руководитель, принимающий решения, не может быть универсалом, обладать исчерпывающей информацией обо всех сторонах жизни, поэтому ему приходится привлекать экспертов.

Эксперты имеют свои предпочтения, поэтому может сложиться ситуация, когда при проведении экспертизы эксперт будет сообщать недостоверную информацию.

Это может происходить, например, в следующих случаях. Пусть собрались эксперты для принятия решения в некоторой области. В ходе обсуждения один из экспертов видит, что решение, которое они собираются принять, сильно отличается от того, что он считает нужным сделать. Например, принимают решения, куда вкладывать деньги университета. Один из деканов считает, что нужно покупать вычислительную технику. Но чувствует, что сейчас примут решение о ремонте. И если этот декан раньше считал, что 30 % можно потратить на ремонт, а 70 % – на закупку техники, то он скажет: «Ничего не нужно на ремонт, давайте все отдадим на компьютерную технику». Тем самым исказив информацию (сообщив не свое истинное мнение).

Это тем более существенно, если эксперты решают (или готовят информацию для принятия решений), как разделить деньги между ними или субъектами, интересы которых они лоббируют. Искажение может происходить по благородным и неблагородным мотивам. С точки зрения математического моделирования важно, что искажение информации может иметь место, если каждый из экспертов заинтересован в том, чтобы результат экспертизы (коллективное решение) был как можно ближе к его мнению.

Предположим, что результатом экспертизы является величина 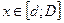, s_i - сообщение i -го эксперта, 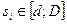, r_i- истинное мнение эксперта, 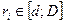. Результат экспертизы - известная функция от мнения экспертов - отображение (процедура экспертизы) 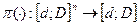множества возможных сообщений во множество возможных решений.

Условия, налагаемые на механизм экспертизы:

1) непрерывность;

2) монотонность;

3) условие единогласия: 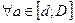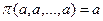. Если все эксперты сообщили одно и то же мнение, то это мнение должно быть принято в качестве коллективного решения.

Рассмотрим сначала пример, а потом приведем общие результаты.

Пример 5.3. Пусть результат экспертизы лежит на отрезке [0;1], и имеются три эксперта. Мнение первого эксперта - оцениваемая величина равна 0,3, второго - 0,5, третьего - 0,7. Процедура экспертизы: берется среднее арифметическое мнений экспертов. Такая функция удовлетворяет всем трем требованиям: легко убедиться, что среднее арифметическое непрерывно, монотонно и удовлетворяет условию единогласия. Итак:

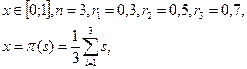
Эксперты будут действовать следующим образом. Пусть все эксперты сообщили правду: 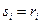. Тогда принимаемое решение будет 0,5 (среднее арифметическое) 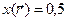. Посмотрим на поведение отдельных экспертов. Каждый эксперт хочет, чтобы результат экспертизы был как можно ближе к его мнению. Второй эксперт абсолютно удовлетворен, так как результат совпадает с тем, что он хочет. Первый недоволен, так как ему требуется меньший результат. Третий эксперт также недоволен, так как он хочет, чтобы результат был больше.

Следовательно, так как функция монотонна, то первый эксперт будет уменьшать сообщение, а третий - увеличивать. Пусть первый говорит 0, второй - 0,5, третий - 1. Тогда результат - 0,5, то есть не изменился, так как насколько первый уменьшил свое сообщение, настолько третий увеличил: s₁= 0, s₂= 0,5, s₃= 1.

Данный вектор сообщений является равновесием Нэша игры экспертов, так как второй эксперт сообщение менять не будет, первый хотел бы сделать результат поменьше, но сделать этого не может, так как сообщает минимум, третий хотел бы сделать результат побольше, но сделать этого не может, так как сообщает максимум. Аналогично в других ситуациях равновесия: кто хочет меньше - не может, так как «упирается» в нижнее ограничение; кто хочет больше - не может, так как «упирается» в верхнее ограничение.

Значит, в общем случае агенты сообщают недостоверную информацию. Спрашивается, можно ли сделать что-то, чтобы побудить их сообщать свои истинные мнения?

Утверждение 5.3. (аналогично утверждению 5.1 для механизмов распределения ресурса).

1) если в равновесии решение оказывается больше, чем мнение некоторых экспертов: x^*>r_i, то эти эксперты в равновесии будут сообщать минимальную оценку: s_i^*=d;

2) если в равновесии решение оказывается меньше, чем мнение некоторых экспертов: x^*<r_i, то эти эксперты в равновесии будут сообщать максимум: s_i ^*= D;

3) если в равновесии некоторые эксперты сообщают мнение, не равное границам отрезков: 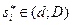, то это значит, что принимаемое решение их устраивает: x^*=r_i.

Опираясь на утверждение 5.3, можно построить равновесие в механизме экспертизы и исследовать его.

Упорядочим экспертов по возрастанию их мнений: . В ситуации, если на отрезке [d;D] было принято некоторое решение, то в соответствии с утверждением 5.3 те эксперты, мнения которых расположены левее принятого решения, будут сообщать нижнюю границу, те, кто правее - верхнюю. Значит, вектор равновесных сообщений будет иметь вид:

s^*=(d,d,...,d,s_k ^*, D,D,...,D).

Эксперты с «маленькими» номерами хотят сдвинуть равновесие влево и сообщают минимальные заявки; быть может, какой-то эксперт с номером k сообщает s_k ^*из отрезка [d;D], эксперты с большими номерами хотят сдвинуть равновесие вправо и сообщают максимальные заявки.

Равновесное сообщение s_k ^* должно быть таким, чтобы выполнялось: .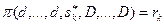

Данное уравнение позволяет найти вектор равновесных сообщений агентов. Но здесь неизвестно, на какой позиции находится s_k: сколько агентов сообщают максимальное значение, а сколько - минимальное, а какой (один или ни одного) эксперт сообщает отличную от границ оценку. Если центр будет это знать, то, подставив s_k, решив это уравнение, он сможет найти вектор равновесных сообщений.

В рассмотренном выше примере k-ым экспертом является второй. Он рассчитывает, если первый говорит - 0, а третий - 1, то, что необходимо сказать ему, чтобы итоговое решение было 0,5? Сообщение должно быть 0,5. Такой эксперт называется диктатором. Чтобы найти его номер в общем случае, введем последовательность чисел:

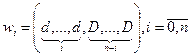Фиксируем число экспертов, сообщающих минимальные мнения, остальные сообщают максимальные. Варьируя число экспертов, которые сообщают минимальные заявки, от 0 до n, получаем убывающую последовательность точек. Точка w₀ совпадает с правой границей D, поскольку, если все сообщили правую границу, то в силу условия единогласия такое решение и будет принято. Аналогично, если все сообщили нижнюю оценку d, то решение равно w_n = d.

Имеются две последовательности чисел: первая – возрастающая последовательность истинных мнений экспертов { r_i }; вторая – убывающая последовательность точек { w_i }. Утверждается, что рано или поздно эти последовательности пересекутся. Найдем крайнюю правую точку пересечения этих последовательностей, то есть нужно взять минимум из этих двух чисел, соответствующих одному и тому же номеру, и взять максимум по всем номерам. Следовательно, существует эксперт с номером: .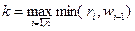

В рассмотренном выше примере: для первого агента – минимум из его мнения и его действия равен r ₁, для второго – r ₂, для третьего агента происходит «поворот» – минимум равен 1/3. Максимум из этих трех точек равен 0,5. Значит, формула дает номер того эксперта, который будет диктатором. В примере k =2.

Предположим, что используется не исходный – 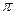– механизм, а экспертам предлагается следующий прямой механизм экспертизы: итоговое мнение будет определяться по вашим сообщениями 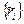в соответствии с процедурой (где сообщения 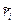сначала упорядочиваются по возрастанию): .