Задачи формирования организационных иерархий

Лекция 7. Механизмы формирования оптимальных структур управления

В лекции формулируются и решаются задачи анализа и синтеза структур управления; в том числе, описываются: задача формирования организационных иерархий (раздел 7.1), модели организационных структур (раздел 7.2), общая модель иерархии управления (раздел 7.3), методы поиска оптимальных древовидных структур (раздел 7.4).

Как изучать организации? Этот на первый взгляд простой и даже странный вопрос (ведь организации изучаются с античных времен) при ближайшем рассмотрении оказывается совсем не простым и вполне уместным. Дело в том, что организации – пожалуй, самая сложная, разнообразная, изменчивая и, как следствие, наименее изученная из известных в настоящее время «форм жизни».

Разнообразие типов, видов, форм организаций растет постоянно и ускоренно, что не позволяет создать в настоящее время сколько-нибудь общей концепции или теории. Даже наиболее постоянные из известных типов организаций, такие как семья, этнос, государство, претерпевают в последние десятилетия столь значительные изменения, что описывающие их теории часто противоположны.

Что же касается организаций, связанных с производственной деятельностью, то их изменение является прямым следствием их существования, точнее – следствием расширенного воспроизводства. Стремительно развивающиеся в последние десятилетия глобальные сетевые (в том числе, виртуальные) организации, на наших глазах объединяющиеся в интернет-сообщества, создающие интернет-экономику и интернет-культуру, то есть – глобальный интернет-социум, служат ярким примером сказанного.

Формальные модели организаций начали активно разрабатываться с середины XX века вследствие, с одной стороны, практической потребности управления все усложняющимися экономическими, социальными и военными организациями, а с другой стороны, – появления новой научной методологии исследования сложных систем – системного подхода и системного анализа. С этого времени организации являются предметом приложения и источником развития математических методов (таких как методы оптимизации, исследование операций, теория игр и др.).

Происшедшая в то же время компьютерная революция создала техническую базу нового математического метода – математического моделирования с его новым исследовательским аппаратом – численным экспериментом, и одной из задач численных экспериментов стало моделирование функционирования организаций.

Созданные к настоящему времени модели организаций, в основном, можно разделить на «экономические» и «инженерные».

В течение первой половины XX века происходил непрерывный процесс формализации экономической науки, который в результате привел к созданию развернутой математической теории экономического равновесия. Однако довольно скоро стало ясно, что эта теория, во-первых, не может объяснить многих наблюдаемых на реальных рынках эффектов, а, во-вторых, почти не рассматривает закономерности внутренней организации экономических субъектов – фирм. Последовательное совершенствование экономической теории во второй половине XX века привело к осознанию важности информационных аспектов функционирования экономических систем, таких, например, как асимметричная информированность агентов и ограниченные их возможности по обработке информации и принятию решений. В числе прочего неоклассическая экономическая теория позволила пролить свет на роль и место иерархических организаций в процессах производства и распределения благ.

Параллельно с развитием математической экономики первая половина XX века была отмечена бурным прогрессом теории управления техническими системами. Развитие авиации и ракетной техники, связанное с созданием и эксплуатацией сложнейших технических систем, породило насущную необходимость в формальных моделях организации их разработки и функционирования. Моделирование сложной технической системы невозможно без ее декомпозиции на более простые подсистемы, позволяющей сначала исследовать поведение изолированных подсистем, а затем описать их взаимосвязи. Многоуровневая декомпозиция позволяет представить сложный объект в виде иерархии вложенных друг в друга более простых частей, задающих его структуру, и от того, насколько удачно выбрана структура проектируемой системы, во многом зависят и ее эксплуатационные характеристики. Поэтому количество исследований, посвященных методам оптимизации структуры технических систем, непрерывно росло. Успешное применение результатов этих работ в практике проектирования и управления техническими системами породило стремление расширить область их применения на организационные и биологические системы, что, в числе прочего, и было реализовано в ходе развития новых научных направлений – кибернетики и теории систем.

В настоящее время наблюдается сближение позиций экономического и инженерного направлений в моделировании организаций. Не последнюю роль в этом сыграло развитие информационных технологий и вычислительной техники. Оказалось, что связанная с обработкой информации работа распределенных вычислительных систем во многом напоминает работу менеджеров в организациях, и в настоящее время многие экономисты используют при моделировании организационных иерархий терминологию и результаты, пришедшие из инженерных наук, в частности, информатики. Таким образом, можно говорить о появлении синтетических теорий, объединяющих достоинства инженерного и экономического подходов.

Любая экономическая система состоит из множества организованных некоторым образом агентов (сотрудников). Благодаря организации сотрудники действуют на основе определенных процедур и правил (механизмов), что позволяет достичь цели системы.

Специализация сотрудников организации повышает их эффективность по сравнению с множеством одиночных (неорганизованных) агентов. Однако взаимодействие сотрудников с различной специализацией должно быть скоординировано для достижения общей цели. Это фундаментальная проблема любой организации, поскольку координация требует усилий, направленных на планирование совместной работы, контроль ее результатов, согласование целей отдельных сотрудников и т.д. Для реализации управленческих функций в организации создается иерархия (сотрудники на более высоких уровнях иерархии обладают бóльшими правами, чем сотрудники нижних уровней, что позволяет системе достичь цели даже в случае конфликтов.).

С одной стороны, иерархия повышает эффективность взаимодействия сотрудников, например, с помощью планирования и контроля материальных, информационных и других потоков. С другой стороны, реализация управленческих функций требует затрат. В современных экономических системах доля менеджеров, выполняющих только управленческие функции, достигает 40 %. Поэтому одним из ключевых факторов эффективности экономической системы является оптимальность иерархии управления.

В реальных организациях возможности эксперимента со структурой управления очень ограничены, поэтому важное значение приобретают модели, которые позволяют выбрать эффективную организационную иерархию, а также обосновать необходимость и направление ее реформирования при изменении условий функционирования организации.

Классификация моделей иерархических структур. Подходы к формулировке и решению задач формирования организационных иерархий весьма разнообразны. Не в последнюю очередь это связано со сложностью описываемого объекта. Разобраться во всем многообразии моделей помогает их классификация. В литературе встречаются несколько принципов систематизации моделей формирования организационных структур. Так, ряд классификаций основывается на формальных характеристиках моделей: используемом математическом аппарате, типах рассматриваемых структур и т.п.

Например, выделяются четыре основных подхода к построению моделей формирования организационных структур. Первый подход основан на построении графа декомпозиции целей и задач организации.В общей теории систем считается, что структура организации во многом обусловлена структурой этого графа. Задача формирования организационной структуры при этом сводится к решению задачи назначения – распределения подцелей по подразделениям и сотрудникам организации. Во втором подходе считается, что задача организации состоит в максимизации некоторого критерия эффективности – ее «целевой функции». В силу сложности этой функции, задачу максимизации приходится декомпозировать и поручать решение частных задач отдельным подразделениям организации. Формирование организационной структуры сводится к поиску допустимой декомпозиции, минимизирующей потери эффективности. В третьем подходе строится функция, напрямую определяющая зависимость эффективности функционирования организации от структурных характеристик организационной иерархии и ищется иерархия, максимизирующая/минимизирующая эту функцию. Четвертый подход связан с количественной оценкой взаимосвязей между элементами системы и иерархической группировкой наиболее сильно связанных элементов в подразделения.

Еще одна система классификации, основана на таких формальных характеристиках моделей, как цель исследования, целенаправленность системы и отдельных ее элементов, однородность элементов, количество уровней организационной структуры, и т.п. Эта довольно подробная система классификаций позволяет разбить все множество моделей на большое количество классов и анализировать, например, степень похожести моделей по различным признакам классификации.

Другие известные системы классификации базируются не на формальных, а на содержательных характеристиках моделей. Наиболее типичным признаком классификации являются задачи, решаемые менеджерами – элементами иерархии управления. Задачи, решаемые менеджерами, могут быть положены в основу классификации моделей формирования иерархий потому, что в рамках одной модели обычно рассматривается только один из видов управленческой работы – тот, который авторы модели принимают за наиболее важный. Среди этих задач Р. Раднер выделяет следующие:

1) наблюдение за внешней средой и результатами предыдущих действий;

2) обработка и передача информации;

3) принятие решений;

4) контроль;

5) решение кадровых вопросов;

6) обучение и разъяснение;

7) планирование;

8) решение проблем;

9) убеждение, принуждение и целеполагание.

Далее в настоящей лекции на примере модели надстройки иерархии управления над технологической сетью проиллюстрируем основные термины и понятия, связанные с организационными структурами.

З адача надстройки иерархии управления над технологической сетью. Пусть N ={ w ₁,…, w_n } – множество исполнителей, которые могут взаимодействовать друг с другом. Через w_env будем обозначать внешнюю среду, взаимодействующую с исполнителями. Иногда исполнители будут обозначаться через .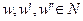

Функцией потока называется следующая функция:

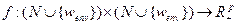(7.1)

то есть для каждой пары исполнителей 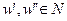вектор 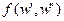определяет интенсивность потоков между и . Этот вектор содержит p неотрицательных компонент. Каждая компонента определяет интенсивность одного типа взаимодействия исполнителей (материальный, информационный или прочий тип потока). Таким образом, технология взаимодействия исполнителей определяет функцию потока f или взвешенную технологическую сеть (N, f). Технологическая сеть считается неориентированной, то есть .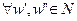

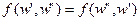Будем говорить, что между парой исполнителей отсутствует связь тогда и только тогда, когда поток между исполнителями нулевой. Предполагаем, что сеть не содержит петель, то есть для любого исполнителя w выполнено f (w, w)= 0.

Рассмотрим пример. Пусть N={w ₁, w₂, w₃} и p= 1, то есть имеются трое исполнителей и потоки одного типа. Будем считать, что в технологической сети имеются четыре связи 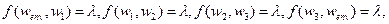, где 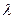- вектор интенсивности потока. Эта технологическая сеть изображена на рисунке 7.1. Данный пример может соответствовать производственной линии («бизнес-процессу»). Исполнитель w₁ принимает сырье от поставщика, проводит первичную обработку и передает результат исполнителю w₂. Тот выполняет очередную технологическую операцию и передает результат далее. Последний исполнитель (в примере - w₃), выполнив последнюю технологическую операцию, отгружает продукцию потребителю.

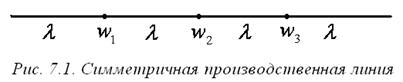
Сеть с исполнителями N = {w ₁, …, w_n} и потоками 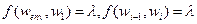для всех 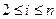, 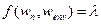будем ниже называть симметричной производственной линией (все остальные потоки подразумеваются равными нулю), а 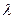- интенсивностью линии.

Обозначим через M конечное множество менеджеров, управляющих взаимодействием исполнителей. Менеджеры обычно будут обозначаться через .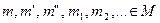

Пусть 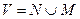- все множество сотрудников организации (исполнителей и менеджеров). Рассмотрим множество ребер подчиненности 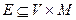. Ребро 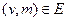означает, что сотрудник 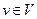является непосредственным подчиненным менеджера 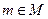, а m - непосредственным начальником сотрудника v. Таким образом, ребро направлено от непосредственного подчиненного к его непосредственному начальнику.

Сотрудник 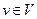является подчиненным менеджера 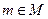(менеджер m является начальником сотрудника v), если существует цепочка ребер подчиненности из v в m. Будем также говорить, что начальник управляет подчиненным, или подчиненный управляется начальником. Дадим строгое определение иерархии.

Определение 7.1. Ориентированный граф 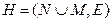с множеством менеджеров M и множеством ребер подчиненности 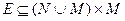назовем иерархией, управляющей множеством исполнителей N, если граф H ацикличен, любой менеджер имеет подчиненных и найдется менеджер, которому подчинены все исполнители. Через 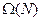обозначим множество всех иерархий.

Ацикличность означает, что не существует «порочного круга» подчиненности, в котором каждый менеджер является одновременно и начальником, и подчиненным всех остальных. Определение 7.1 также исключает ситуации, в которых имеются «менеджеры» без подчиненных, так как это противоречит роли менеджера, который должен управлять некоторыми сотрудниками.

Существование менеджера, которому подчинены все исполнители, означает, что у любого множества исполнителей найдется общий начальник, то есть иерархия способна управлять взаимодействием всех исполнителей.

Рис. 7.2 иллюстрирует введенное определение. Исполнители на нем изображены темными кружками и пронумерованы арабскими цифрами, а менеджеры изображены светлыми кружками и пронумерованы латинскими цифрами. Графы а)-в) являются иерархиями, управляющими множеством исполнителей N ={1, …, 4}. Определенные таким образом иерархии позволяют описывать часто встречающиеся в практике управления эффекты, например, межуровневое взаимодействие, когда менеджер непосредственно управляет и другими менеджерами, и исполнителями (менеджер II иерархии б), а также множественное подчинение, когда сотрудник имеет более одного непосредственного начальника (менеджер I в иерархии б), исполнитель 3 в иерархии в). Определение 7.1 допускает наличие в иерархии нескольких менеджеров, не имеющих начальников (менеджеры II и III иерархии б), а также менеджеров, имеющих единственного непосредственного подчиненного (менеджер III иерархии б).

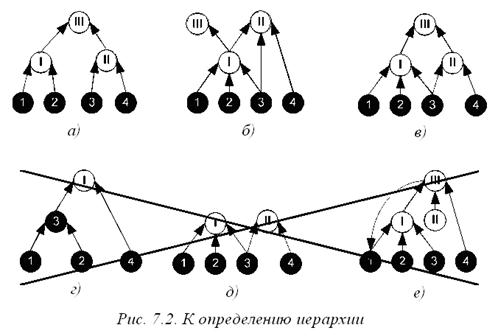
В то же время, графы г)-е) иерархиями не являются. В графе г) исполнитель с номером 3 имеет подчиненных, в графе д) нет топ-менеджера, который управлял бы всеми исполнителями, в графе е) менеджер II не имеет подчиненных, кроме того, этот граф содержит цикл .

Определим несколько частных видов иерархии и введем важное понятие нормы управляемости.

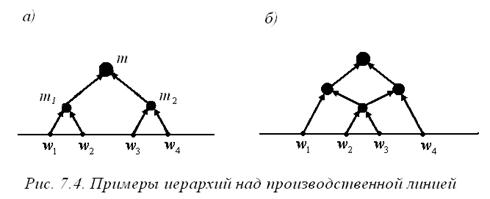
Определение 7.2. Иерархию назовем деревом, если в ней только один менеджер m не имеет начальников, а все остальные сотрудники имеют ровно одного непосредственного начальника. Менеджера m будем называть корнем дерева.

На рисунке 7.4 a) изображен пример дерева. Напротив, иерархия 7.4 б) деревом не является, так как в ней один менеджер имеет двух непосредственных начальников.

Определение 7.3. Иерархию назовем r -иерархией, если у каждого ее менеджера не более r непосредственных подчиненных, где r >1 – целое число. r -иерархию, которая является деревом, назовем r- деревом.

В литературе по менеджменту часто используется термин «норма управляемости» – максимальное количество непосредственных подчиненных, которыми может управлять один менеджер. Определение r -иерархии соответствует норме управляемости, равной r. В силу леммы 7.2 в дереве норма управляемости не превосходит n. Максимальную среди всех деревьев норму управляемости имеет двухуровневая иерархия, в которой одному менеджеру непосредственно подчинены все исполнители.

Определение 7.4. Двухуровневой ( веерной ) иерархией называется иерархия с единственным менеджером, который непосредственно управляет всеми исполнителями.

Определение 7.5. Последовательной иерархией называется 2-иерархия, в которой каждый менеджер непосредственно управляет, как минимум, одним исполнителем.

Основным для организационных структур понятием является понятие сферы ответственности менеджера (его обязанностей). Для формализации «роли» менеджера в организации введем понятие группы, управляемой менеджером.

Группой исполнителей 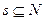называется любое непустое подмножество множества исполнителей.

По определению 7.1 в любой иерархии H каждый менеджер имеет, по крайней мере, одного непосредственного подчиненного. Начав с любого менеджера m, мы можем двигаться по иерархии «сверху вниз» к подчиненным менеджера m. В итоге можно определить множество исполнителей, подчиненных менеджеру m. Будем называть это множество подчиненной группой исполнителей и обозначать 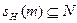. Будем также говорить, что менеджер m управляет группой исполнителей s_H (m). Ниже в обозначении группы s_H (m) будем опускать нижний индекс, если ясно, о какой иерархии идет речь.

Также будем считать, что исполнитель 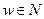«управляет» простейшей группой s_H (w)={ w }, состоящей из него самого.

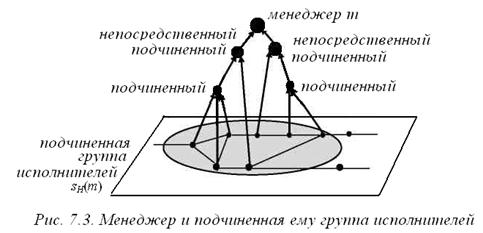
На рис. 7.3. плоскость соответствует технологической сети, над которой надстраивается иерархия. Над плоскостью изображена часть иерархии, подчиненная менеджеру m. Она состоит из непосредственных подчиненных менеджера m и подчиненных, которыми менеджер m не управляет непосредственно. Подчиненная группа исполнителей s_H (m) обведена на рисунке эллипсом.

Сформулируем простую лемму, необходимую для дальнейшего изложения.

Лемма 7.1. Для любой иерархии H и любого менеджера 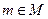выполнено , где v ₁, …, vk - все непосредственные подчиненные менеджера m. Для любого подчиненного v менеджера m выполнено .

Проиллюстрируем результат леммы на примере. На рисунке 7.4 a) менеджеру m непосредственно подчинены менеджеры m₁ и m ₂. Менеджеру m подчинена группа s (m)={ w ₁, w ₂, w ₃, w ₄}. Менеджерам m₁ и m ₂ подчинены группы s(m₁)={w ₁, w₂} и s (m ₂)={ w ₃, w₄} соответственно. Таким образом, группа s(m) разбивается на две подгруппы s (m₁) и s (m ₂): 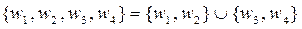. В данном примере подгруппы не пересекаются. В общем случае, как показано на рисунке 7.4 б), пересечения могут иметь место.

Сформулируем полезную лемму – критерий древовидности иерархии.

Лемма 7.2. Пусть в иерархии H только один менеджер не имеет начальников. Иерархия H будет деревом тогда и только тогда, когда непосредственные подчиненные любого менеджера управляют непересекающимися группами исполнителей.

Таким образом, при наличии единственного менеджера без начальников в дереве и только в нем непосредственные подчиненные любого менеджера не «дублируют» обязанности друг друга, то есть не управляют одним и тем же исполнителем.

В рассматриваемой модели объем выполняемой менеджером работы определяется потоками технологической сети между исполнителями управляемой им группы и потоками между управляемой группой исполнителей и остальной организацией. Считается, что любой менеджер выполняет обязанности двух типов:

1) Управляет теми потоками внутри подчиненной группы, которые не управляются подчиненными менеджерами. Например, на рисунке 7.4 а) менеджер m управляет потоком f (w ₂, w ₃).

2) Участвует в управлении потоками между подчиненной группой и всеми остальными исполнителями, внешней средой. Эта компонента потока указана в приведенных выше выражениях в скобках. Например, на рисунке 7.4 а) менеджер m ₁ участвует в управлении потоками f (w_env, w ₁) и f (w ₂, w ₃).

Введем формальное определение обязанностей менеджера.

Определение 7.6. В иерархии менеджер m выполняет обязанности двух типов:

1) Управляет потоками 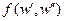между подчиненными исполнителями 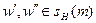, которые не управляются ни одним из подчиненных менеджера m. Сумму таких потоков назовем внутренним потоком менеджера m и обозначим F_H ^int (m).

2) Участвует в управлении потоками f(w ', w '' ) между подчиненным исполнителем 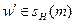и неподчиненным исполнителем 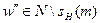или внешней средой w '' =w_env. Сумму таких потоков назовем внешним потоком менеджера m и обозначим F_H^ext(m).

Таким образом, менеджер управляет внутренним потоком и участвует в управлении внешним. Потоком менеджера назовем сумму его внутренних и внешних потоков.

Из определения 7.6 следует, что внешний поток менеджера m равен:

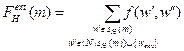. (7.2)

Величина внутреннего потока определяется следующей леммой.

Лемма 7.3. Пусть v₁, …, v_k - все непосредственные подчиненные менеджера m в иерархии H. Тогда внутренний поток менеджера m равен:

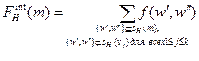. (7.3)

Таким образом, при суммировании потоков f(w ', w '' ) внутри группы s_H(m) достаточно проверить, чтобы поток не входил в группы, управляемые непосредственными подчиненными. В этом и только в этом случае поток не будет управляться ни одним подчиненным менеджера, то есть будет входить в его внутренний поток.

Получим, что при заданных N и f внутренний и внешний поток менеджера m зависит только от s_H (v ₁),..., s_H (v_k), то есть от групп исполнителей, которыми управляют непосредственные подчиненные менеджера m.

По определению 7.1 в любой иерархии H найдется менеджер m, управляющий всеми исполнителями (топ-менеджер). Поэтому каждый поток внутри технологической сети управляется либо топ-менеджером, либо его подчиненными. Таким образом, любая иерархия обеспечивает управление всеми потоками.

Однако в различных иерархиях различается количество менеджеров и «нагрузка» каждого из менеджеров. Поэтому из всего множества иерархий 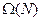необходимо выбрать иерархию, наилучшую с точки зрения некоторого критерия. В качестве такого критерия рассмотрим управленческие расходы - суммарные затраты на содержание всех менеджеров иерархии. В базовой модели будем считать, что затраты на содержание менеджера зависят только от суммы потоков, которыми он управляет, и в управлении которыми он участвует. Сформулируем строгое определение.

Определение 7.7. Затратами менеджера 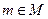в иерархии 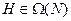назовем величину:

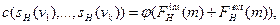(7.4)

где v ₁, …, v_k - все непосредственные подчиненные менеджера m, s_H (v ₁), …, s_H (v_k) - управляемые ими группы, 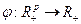- монотонно неубывающая по всем переменным функция, ставящая в соответствие вектору 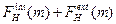затраты менеджера.

Суммарные затраты всей иерархии складываются из затрат менеджеров. Оптимальной будет та иерархия, которая минимизирует суммарные затраты. Дадим строгое определение.

Определение 7.8. Затратами иерархии 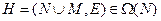назовем сумму затрат всех ее менеджеров:

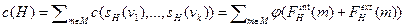, (7.5)

где v ₁, …, v_k - все непосредственные подчиненные менеджера m.

Оптимальной иерархией назовем иерархию H^*, затраты которой минимальны: .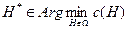

Считаем, что после нахождения оптимальной иерархии можно принять на работу менеджеров, которые будут выполнять свои обязанности, если им компенсировать их затраты (например, выплачивать зарплату), затраты могут включать не только зарплату менеджера, но и затраты на организацию его работы – рабочее место, обслуживающий персонал и т.д. Разумеется, для этого необходима полная информация о функции затрат. Ниже функция 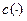затрат менеджера предполагается известной. Эта функция может определяться непосредственно по данным о затратах менеджеров. Кроме того, можно рассматривать некоторые «типичные» функции затрат (например, ниже исследуется степенная функция). При этом подбираются параметры, при которых значения функции в наибольшей степени соответствуют реальным затратам менеджеров. Затраты могут измеряться, например, в денежном эквиваленте приложенных усилий, исходя из средней заработной платы менеджеров на соответствующих позициях

Очевидно, что даже в простейших случаях множество всевозможных иерархий настолько обширно, что отыскание оптимальной иерархии методом перебора всех вариантов требует огромных вычислительных ресурсов. Ниже будут изложены методы, которые при определенных ограничениях позволяют найти оптимальную иерархию, либо сузить множество иерархий, в котором содержится оптимальная.

Утверждение 7.1. Для любой иерархии 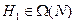найдется иерархия 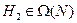, имеющая не бóльшие затраты 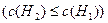, и удовлетворяющая следующим свойствам:

I. все сотрудники управляют различными группами исполнителей;

II. только один менеджер не имеет начальников. Этому менеджеру подчинены все остальные менеджеры и все исполнители;

III. среди сотрудников, непосредственно подчиненных одному менеджеру, ни один не управляет другим.

Если H ₁ – r- иерархия, дерево или r- дерево, то и H ₂ будет соответственно r- иерархией, деревом или r- деревом.

Доказательство утверждения 7.1 основано на последовательном перестроении H ₁ без увеличения затрат. В итоге перестроений получаем иерархию H ₂, которая удовлетворяет условиям (I-III). Для r -иерархии, дерева и r- дерева перестроения не изменяют вида иерархии.

Условие (I) означает отсутствие полного дублирования, при котором два менеджера управляют одной и той же группой исполнителей. На рисунке 7.5 а) приведен пример подобного дублирования. Два менеджера управляют одной и той же группой { w ₁, w ₂, w ₃}. При этом один них может быть удален, а всем его непосредственным начальникам можно подчинить другого менеджера без увеличения затрат. В частности, из условия (I) следует, что у любого менеджера имеется не менее двух непосредственных подчиненных (иначе в силу леммы 7.1 он управлял бы той же группой, что и его единственный непосредственный подчиненный).

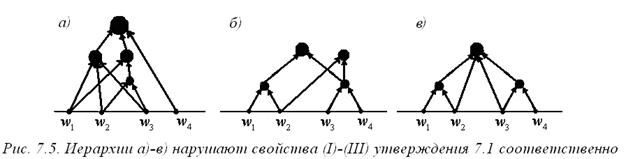
В соответствии с условием (II) найдется только один менеджер m, который не имеет начальников. Этому менеджеру подчинены все исполнители 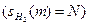ивсе остальные менеджеры иерархии. Будем называть m высшим менеджером или топ-менеджером.

Условие (II) соответствует практике построения организаций, при которой только один высший менеджер может принимать решения, обязательные для всех сотрудников (например, может разрешить конфликт между любыми сотрудниками). На рисунке 7.5 б) приведен пример, в котором два менеджера не имеют начальников, то есть нарушается условие (II). Очевидно, что «лишний» менеджер может быть удален без увеличения затрат иерархии.

Условие (III) можно интерпретировать следующим образом. Пусть менеджер m ₁ непосредственно подчинен менеджеру m. Тогда m непосредственно не управляет подчиненными менеджера m₁. Это соответствует «нормальному» функционированию организации, при котором менеджер управляет всеми подчиненными сотрудниками через непосредственных подчиненных, а не напрямую. На рисунке 7.5 в) приведен пример, в котором высший менеджер m непосредственно управляет исполнителями w₂ и w₃, несмотря на то, что ими уже управляют непосредственные подчиненные m ₁ и m₂ менеджера m. Ребра (w₂, m) и (w₃, m) могут быть удалены без увеличения затрат иерархии.

Из утверждения 7.1 следует, что найдется оптимальная иерархия, удовлетворяющая условиям (I)-(III)³³. Этот факт позволяет в ряде случаев значительно упростить задачу поиска оптимальной иерархии, поскольку можно не рассматривать иерархии, нарушающие хотя бы одно из условий (I)-(III).

Кроме того, утверждение 7.1 позволяет доказать следующий факт. Если существует оптимальная r -иерархия, дерево или r- дерево, то существует оптимальная иерархия соответствующего вида, удовлетворяющая условиям (I)-(III).

Рассмотрим условие, при котором оптимальна простейшая двухуровневая иерархия.

Утверждение 7.2. Пусть функция затрат 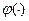субаддитивна, то есть для всех 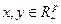выполнено неравенство . Тогда оптимальна двухуровневая иерархия.

Условие субаддитивности означает, что затраты 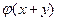одного менеджера на управление суммарным потоком x+y не больше, чем затраты двух менеджеров на управление частями этого потока x и y. В этом случае оптимальна простейшая двухуровневая иерархия, в которой все потоки управляются одним менеджером.

Из утверждения 7.2 следует, что вогнутость функции затрат влечет оптимальность двухуровневой иерархии, если все потоки технологической сети однотипны (то есть вектор потока содержит одну компоненту).

В небольших организациях весьма распространены двухуровневые иерархии (так называемые «простые структуры»). При росте организации единственный менеджер чрезмерно загружен, что вынуждает его принимать на работу «помощников» - переходить к многоуровневой иерархии.

Одним из интересных вопросов является оптимальность древовидной иерархии, которая встречается в реальных организациях наиболее часто. Пример 7.1 ниже показывает, что иногда оптимальная иерархия не является деревом.

Пример 7.1 (снижение затрат при множественном подчинении для несимметричной линии). Пусть в несимметричной производственной линии имеется четыре исполнителя и потоки f (w_env, w ₁)=3, f (w ₁, w₂)=1, f (w ₂, w ₃)=5, f (w ₃, w ₄)=1, f (w ₄, w_env)=3. Рассмотрим следующую функцию затрат менеджера: 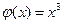(x - величина потока менеджера) - см. выражение (7.4). Оптимальная иерархия для этого примера изображена на рисунке 7.6. Обозначим ее через H. У менеджера m₁ два непосредственных начальника, то есть в оптимальной иерархии имеет место множественное подчинение.

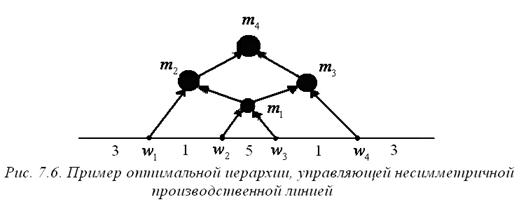
Определим потоки каждого менеджера:

;

;

;

.

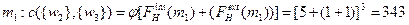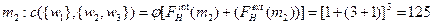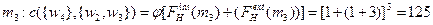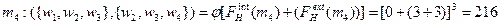Таким образом, затраты всей иерархии составят:

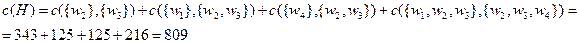
Убедимся, что найденные затраты являются минимально возможными. Пусть H^* – оптимальная иерархия, удовлетворяющая условиям (I)-(III) утверждения 7.1. В H^* должен быть хотя бы один менеджер m нижнего уровня, которому не подчинены другие менеджеры.

Если m управляет тремя или более исполнителями, то величина потока m не менее 10. Таким образом, затраты m не менее 1000, что больше, чем c (H)=809. Следовательно, m управляет ровно двумя исполнителями.

Если m управляет двумя исполнителями, идущими в производственной линии не подряд (например, w ₁ и w ₃), то 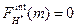, то есть m не управляет ни одним внутренним потоком, а лишь участвует в управлении внешними. Тогда можно удалить менеджера m, подчинив исполнителей из 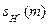непосредственным начальникам m, причем их затраты не изменятся, что противоречит оптимальности H^*. Таким образом, менеджеру m могут быть подчинены только два исполнителя, идущие в линии подряд.

Если менеджеру m подчинены исполнители w ₁ и w ₂ (или w ₃ и w ₄), то его затраты составляют 9³ = 729. Кроме того, высший менеджер по крайней мере участвует в управлении внешними потоками, следовательно его затраты не менее 6³=216. То есть в этом случае с (H^*)>729+216=945, что противоречит оптимальности H^*. Таким образом, в H^* имеется ровно один менеджер m нижнего уровня. Менеджер m управляет исполнителями w ₂ и w ₃, то есть наибольшим потоком f (w ₂, w ₃)=5.

Рассматриваемый пример иллюстрирует общее правило: потоки наибольшей интенсивности должны управляться на нижних уровнях иерархии. Это правило отмечается во многих работах по менеджменту на основании опыта исследования реальных организаций. В примере рассмотрен предельный случай, в котором для управления наибольшим потоком специально должен быть выделен менеджер нижнего уровня.

Так как m - единственный менеджер нижнего уровня, то он подчинен всем остальным менеджерам иерархии(каждому отличному от m менеджеру m' непосредственно подчинен некоторый менеджер m'' (иначе m' – менеджер нижнего уровня, то есть m'= m). Если m''¹ m, то можно повторить рассуждения. В итоге дойдем до m, то есть докажем его подчиненность менеджеру m'.). Тогда исполнители w₂ и w ₃ непосредственно подчинены только менеджеру m, так как иначе нарушается условие (III) утверждения 7.1. То есть после назначения менеджера m оптимальная иерархия H* надстраивается над 3 сотрудниками: w ₁, m, w₄. Тогда кроме иерархии H (см. рисунок 7.6.) имеем три варианта иерархии, удовлетворяющие условиям (I)-(III) утверждения 7.1. Эти иерархии изображены на рисунке 7.7.

Легко вычислить, что с (H ₁)= с (H ₃)=811, c (H ₂)=855. В силу того, что с (H)=809, все иерархии на рисунке 7.7 неоптимальны, следовательно, H = H^* – единственная оптимальная иерархия.

Итак, рассмотренный пример показывает, что для технологической сети общего вида среди деревьев может не быть оптимальных иерархий. Ниже оптимальность древовидной иерархии доказана для симметричной производственной линии. Кроме того, в общей модели найдено достаточное условие оптимальности древовидной иерархии. В этих условиях найти оптимальную иерархию позволяют алгоритмы поиска дерева с минимальными затратами.

Пример 7.2. Снижение управленческих затрат при росте организации. Рассмотрим несимметричную производственную линию из четырех исполнителей с потоками f (w_env, w ₁)=1, f (w ₁, w ₂)=5, f (w ₂, w ₃)=1, f (w ₃, w ₄)=5, f (w ₄, w_env)=1 и функцией затрат иерархии 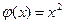(x – величина потока менеджера). Сначала предположим, что к организации относятся только исполнители w ₂ и w ₃, то есть рассмотрим технологическую сеть N ={ w ₂, w ₃}. Тогда существует только одна иерархия, удовлетворяющая условиям утверждения 7.1. Эта иерархия изображена на рисунке 7.8 a).

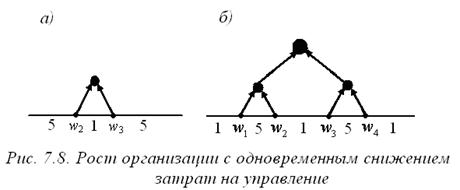
Предположим, что мы имеем возможность расширить организацию, включив в нее еще двух исполнителей w₁ и w₄. Содержательно это можно интерпретировать следующим образом. Например, крупная компания оптовой торговли покупает фирму-производителя товара («исполнителя» w₁)и сеть розничных магазинов («исполнителя» w ₄), стремясь управлять всей линией от производства до конечной реализации товаров. Большой поток f (w ₁, w₂) = 5 может соответствовать, например, потоку информации, который связан с проблемами компании при взаимодействии с производителем (скажем из-за большого количества брака). Аналогично, большой поток f (w₃, w₄)=5 может быть связан с проблемами взаимодействия с розничной сетью, например, с большим числом возвратов товара покупателями.

Таким образом, после расширения организация будет управлять технологической сетью N= { w ₁, w₂, w₃, w₄ }. При этом имеется возможность перестроить иерархию управления так, как показано на рисунке 7.8 б). То есть нанять двух менеджеров нижнего уровня, которые будут ответственны за управление большими потоками. Сравним затраты иерархий:

a) (5 + 1 + 5)² = 121,

b) (1 + 5 + 1)² + (1 + 5 + 1)² + (1 + 1 + 1)² = 49 + 49 + 9 = 107.

Таким образом, затраты на управление могут снизиться при расширении технологической сети (включении новых исполнителей - части внешней среды). Это может служить одной из причин покупки нового бизнеса, который неприбылен сам по себе, но позволяет снизить расходы на управление основным бизнесом. На практике имеется множество подобных фактов. Например, в России в 90-х годах XX века многие заводы пищевой промышленности трансформировались в вертикально интегрированные агропромышленные компании после покупки сельхозпредприятий своего региона, которые не были прибыльными, но позволяли обеспечить бесперебойную поставку дешевого сырья.

Пример 7.3 (многокомпонентные потоки). В силу утверждения 7.2 двухуровневая иерархия оптимальна при вогнутой функции затрат и однокомпонентных потоках. Покажем, что для многомерных потоков это в общем случае не так. Рассмотрим двухкомпонентный поток (p= 2). Первая компонента соответствует материальным потокам, вторая - информационным. Предположим, что N= { w ₁, w₂, w₃, w₄ }и технологическая сеть выглядит так, как показано на рисунке 7.9.

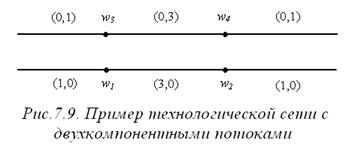
Исполнитель w₁ получает сырье, выполняет технологическую операцию и передает полуфабрикаты исполнителю w₂, который производит сборку готового продукта и его отгрузку клиенту. Величина потока может, например, соответствовать количеству наименований передаваемых материалов. Исполнитель w ₁ получает сырье одного типа и производит из него три типа деталей. Исполнитель w₂ получает эти детали, собирает их и отгружает один тип продукта. Таким образом, внутренний поток f (w ₁, w ₂) превосходит внешние потоки f (w_env, w ₁) и f (w ₂, w_env).

Исполнитель w₄ ведет переговоры с заказчиками, готовит и заключает договора поставки продукции, учитывает оплату и отгрузку продукции и т.п.

Данные о необходимом объеме производства исполнитель w₄ передает исполнителю w₃. На основании полученных данных исполнитель w ₃ размещает заказы сырья, ведет учет его поступления, обеспечивает расчеты и т.п. Также исполнитель w₃ может передавать исполнителю w₄ информацию, необходимую для расчета стоимости и срока выполнения заказа.

Внутренний поток информации f (w ₃, w₄) может превышать внешние потоки f (w_env, w₃) и f (w ₄, w_env), например, за счет большого количества внутренних документов.

Предположим, что функция затрат менеджера имеет вид 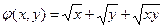, где (x, y) - вектор потока менеджера. Эта функция вогнута, что может соответствовать ситуации, в которой менеджеры не сильно загружены и увеличение управляемого потока снижает затраты на единицу потока. Слагаемое 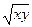может соответствовать специализации менеджеров. Оно равно нулю, если менеджер управляет только потоком одного типа, например производством или документооборотом. В этом случае менеджер становится специалистом в соответствующей области и может управлять потоком с минимальными затратами. Если же менеджер вынужден управлять потоками обоих типов, то его затраты повышаются за счет снижения специализации.

На рисунке 7.10 a) изображена двухуровневая иерархия H ₁. В ней поток единственного менеджера равен (5, 5), то есть затраты иерархии равны .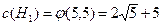

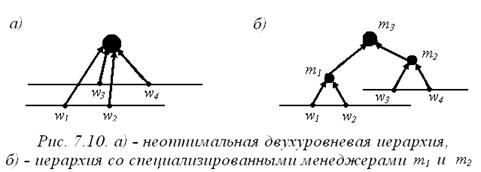
Рассмотрим иерархию H ₂ с тремя менеджерами, которая изображена на рисунке 7.10 б). Менеджер m ₁ управляет только производством, то есть исполнителями w₁ и w₂. Поток менеджера m₁ равен (5, 0). Затраты менеджера m₁ равны 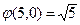. Аналогично, менеджер m₂ управляет только документооборотом, то есть исполнителями w₃ и w₄. Поток менеджера m₂ равен (0, 5). Затраты менеджера m₂ равны 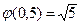. Высшему менеджеру m₃ подчинены менеджеры m₁ и m₂. Менеджер m₃ не вникает в детали потоков внутри технологической сети, а лишь участвует в управлении потоками между технологической сетью и внешней средой, то есть взаимоотношениями с клиентами и поставщиками. Затраты менеджера m₃ равны 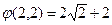. Таким образом, .

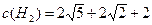В итоге имеем c(H₂) < c(H ₁ ), то есть при многокомпонентных потоках за счет назначения нескольких специализированных менеджеров можно снизить затраты иерархии даже в случае вогнутой функции затрат .

Описанная модель управления технологическими потоками позволяет в ряде случаев аналитически исследовать изменение иерархии, управляющей относительно простой технологической сетью. Не вдаваясь в детали исследования конкретной модели, перейдем к систематическому обзору подходов к математическому моделированию иерархий.