Оптимальные древовидные структуры

Класс секционных функций затрат на управление.

Определение 7.9. Пусть задано множество исполнителей N. Функция затрат менеджера называется секционной, если она зависит только от групп исполнителей, которыми управляют его непосредственные подчиненные.

Таким образом, если менеджер m в иерархии H имеет r непосредственных подчиненных v ₁, v ₂, …, v_r, то его затраты можно записать в виде:

c (m, H)= c (s_H (v ₁), …, s_H (v_r)).

Число аргументов секционной функции затрат равно количеству непосредственных подчиненных менеджера и функция определяется для любого их количества. Значение секционной функции затрат не зависит от порядка следования ее аргументов (групп) и не изменяется при их перестановке. Таким образом, секционная функция затрат ставит в соответствие произвольному непустому множеству групп исполнителей число – затраты менеджера, непосредственные подчиненные которого управляют этими группами исполнителей.

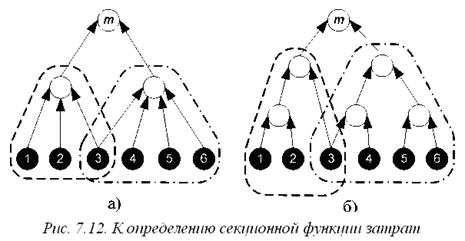
При секционной функции затраты менеджера не зависят от того, как «внутри» организована работа его непосредственных подчиненных, а зависят только от групп исполнителей, которыми те управляют. Так, затраты менеджера m в иерархиях на рисунках 7.12 а) и 7.12 б) одинаковы, поскольку в обеих иерархиях менеджер m имеет двух непосредственных подчиненных, управляющих группами исполнителей {1, 2, 3} и {3, 4, 5, 6}. При этом, понятно, что совокупные затраты этих иерархий могут отличаться.

Например, в модели, описанной в разделе 7.1, затраты менеджера определяются заданными технологическими потоками и функцией . Внутренние и внешние потоки менеджера зависят только от групп, управляемых его непосредственными подчиненными v ₁, …, v_k. Функция затрат менеджера (7.4) зависит только от групп s_H (v ₁), …, s_H (v_k), то есть является секционной. Таким образом, в модели надстройки иерархии управления над технологической сетью рассматривается частный случай секционной функции затрат.

При незначительном техническом ограничении на секционную функцию утверждение 7.1 остается верным и для общей модели. Свойства оптимальных иерархий (І)-(ІІІ) из утверждения 7.1 существенно облегчают поиск оптимальной иерархии: в числе прочего, из них следует, что можно рассматривать только конечные множества допустимых иерархий, и каждый менеджер будет иметь как минимум двух непосредственных подчиненных. Несмотря на это, задача поиска оптимальной иерархии для произвольной секционной функции затрат остается весьма сложной. В то же время, даже для такой общей постановки задачи в ряде случаев удается очень много сказать о виде оптимальной иерархии.

Достаточное условие невыгодности множественного подчинения.

Определение 7.10. Секционная функция затрат менеджера называется монотонной по группам, если затраты любого менеджера не убывают как при расширении групп, управляемых непосредственными подчиненными, так и при добавлении новых непосредственных подчиненных, то есть для любого набора групп s ₁, …, s_r выполнены неравенства: , где группа s содержит ;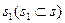

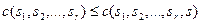, где s – произвольная группа.

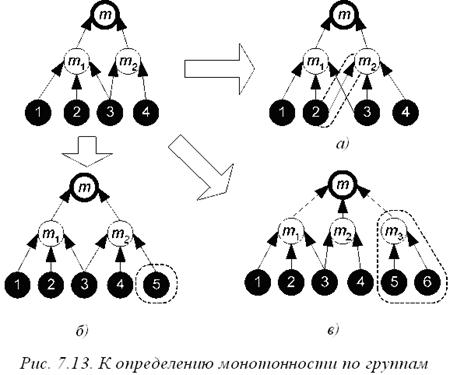
Свойство монотонности по группам иллюстрируется на рисунке 7.13, на котором изображена часть иерархии, подчиненная менеджеру m, имеющему непосредственных подчиненных m ₁ и m ₂.

Стрелками показаны возможные способы расширения групп, управляемых непосредственными подчиненными менеджера m (иерархии 7.13 а) и 7.13 б) и добавления новой подчиненной группы (иерархия 7.13 в). Иерархия 7.13 а) получена из исходной путем расширения группы, подчиненной менеджеру m ₂, за счет подчиненных менеджера m ₁. В иерархии 7.13 б) подчиненная менеджеру m ₂ группа расширяется за счет добавления новых исполнителей. Наконец, в иерархии 7.13 в) менеджеру m добавляется новый непосредственный подчиненный – менеджер m ₃. Добавляемые части иерархии для наглядности обведены штрихованной линией. Функция затрат менеджера будет монотонной по группам, если при любых подобных преобразованиях затраты менеджера m (выделенного на рисунке жирной линией) не уменьшаются.

Утверждение 7.3. Если функция затрат монотонна по группам, то для заданного множества исполнителей N на множестве 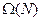всех иерархий существует оптимальное дерево.

Таким образом, если функция затрат менеджера монотонна по группам и на множестве всех иерархий необходимо найти оптимальную, то можно искать ее только среди деревьев. Это позволяет использовать разработанные численные алгоритмы поиска оптимальных деревьев. Для произвольной секционной функции затрат точный алгоритм поиска оптимального дерева имеет довольно высокую вычислительную сложность, позволяя решить задачу не более чем для 15-20 исполнителей (имеется в виду решение задачи персональным компьютером в течение нескольких минут). Однако поиск оптимальной недревовидной иерархии на порядки сложнее даже этой трудоемкой задачи.

По сути, монотонность по группам говорит о неоптимальности так называемого множественного подчинения сотрудников – если функция затрат монотонна по группам, то каждый сотрудник, за исключением топ-менеджера, должен иметь единственного непосредственного начальника.

Условия оптимальности типовых иерархий. Далее рассматриваются условия, при которых оптимальными будут иерархии c минимальной и максимальной возможными нормами управляемости.

Определение 7.11 Секционная функция затрат называется сужающей, если для любого менеджера m с непосредственными подчиненными v ₁, …, v_r при 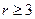можно без увеличения затрат иерархии переподчинить нескольких сотрудников из v ₁, …, v_r новому менеджеру m ₁ и непосредственно подчинить менеджера m ₁ менеджеру m. Секционная функция затрат называется расширяющей, если при любых подобных переподчинениях затраты иерархии не уменьшаются.

Рисунок 7.14 иллюстрирует это определение. На нем слева (иерархия а)) изображена секция менеджера m, состоящая из него самого и его непосредственных подчиненных v ₁, v ₂, v ₃, которые могут быть как менеджерами, так и исполнителями. Справа на рисунке (иерархия б)) изображена та же часть иерархии после переподчинения части непосредственных подчиненных менеджера m (например, сотрудников v ₁ и v ₂) новому менеджеру m ₁ (обведенному на рисунке жирной линией). Если для любого менеджера всегда найдется подобное перестроение, не увеличивающее затраты иерархии, то функция затрат является сужающей. Если же любое такое перестроение не приводит к уменьшению затрат иерархии, то функция затрат является расширяющей.

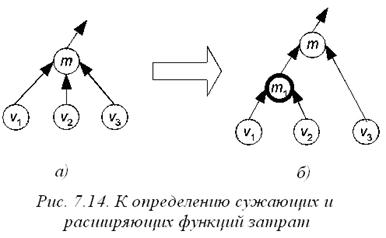
Подчеркнем, что определение требует невозрастания или неубывания затрат всей иерархии. При этом изменение затрат иерархии складывается из затрат добавляемого менеджера m₁ и изменения затрат менеджера m (у него уменьшается количество непосредственных подчиненных). Поэтому для того, чтобы функция затрат была сужающей, как минимум необходимо, чтобы затраты менеджера m не увеличивались при замене нескольких его непосредственных подчиненных менеджером m ₁.

Содержательно определение сужающей функции затрат означает, что при наличии в иерархии менеджера с более чем двумя непосредственными подчиненными всегда выгодно нанять ему «помощника», сняв с менеджера часть его нагрузки. При расширяющей функции затрат, наоборот, всегда выгодно увольнять промежуточных менеджеров. Эти соображения иллюстрируют идею доказательства следующего результата.

Утверждение 7.4 При сужающей функции затрат на множестве 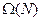существует оптимальная 2-иерархия, при расширяющей функции затрат оптимальна веерная иерархия.

Таким образом, если функция затрат сужающая, то на множестве 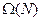(или на произвольном множестве 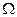, включающем все 2-иерархии) оптимальную иерархию можно искать только среди 2-иерархий. Если функция затрат - расширяющая, и веерная иерархия допустима, то эта иерархия и будет оптимальной.

Если функция затрат одновременно и монотонная по группам, и сужающая, то, пользуясь утверждениями 7.3 и 7.4, несложно показать, что оптимальная иерархия будет 2-деревом. Более того, для монотонной по группам функции затрат определение 7.11 можно ослабить, требуя его выполнения только в случае, когда все сотрудники v ₁, …, v_r управляют непересекающимися группами исполнителей. При выполнении такого ослабленного условия функция затрат называется сужающей на непересекающихся группа х. Для монотонной функции расширение на непересекающихся группах влечет оптимальность веерной иерархии.

Результат утверждения 7.4 использует невозрастание (или неубывание) затрат иерархии при последовательных операциях переподчинения – для сужающей функции каждое переподчинение не увеличивает затрат иерархии, а для расширяющей – не уменьшает их. При этом оптимальными оказываются иерархии, которые не могут быть преобразованы никаким переподчинением. Таким же образом можно вводить и другие преобразования иерархии и пользоваться неубыванием или невозрастанием затрат иерархии относительно них.

Пусть, например, на множестве допустимых иерархий ищется оптимальная иерархия при сужающей функции затрат. Согласно утверждению 7.4 оптимальную иерархию можно искать среди 2-иерархий. Допустим, в некоторой 2-иерархии H менеджер m имеет непосредственно подчиненных ему менеджеров m ₁ и m ₂, причем первый из них управляет некоторым сотрудником v и исполнителем w, а второй – некоторым сотрудником v’ и исполнителем w’ (см. рисунок 7.15 а). У всех этих сотрудников могут быть и другие начальники, не изображенные на рисунке. Обозначим через s ₁ и s ₂ группы, управляемые соответственно менеджерами m ₁ и m ₂.

Преобразуем изображенную на рисунке часть иерархии: удалим связи от менеджеров m ₁ и m ₂ к m, добавим нового менеджера m ₃, которого подчиним менеджеру m и назначим менеджеру m ₃ в непосредственные подчиненные сотрудника v и менеджера m ₂. Кроме того, непосредственно подчиним исполнителя w менеджеру m (см. рисунок 7.15 б). Легко проверить, что при таком преобразовании затраты менеджеров иерархии, не изображенных на рисунке, не меняются, и затраты иерархии изменятся на величину:

.

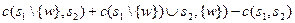Точно такую же операцию можно проделать и с менеджером m ₂.

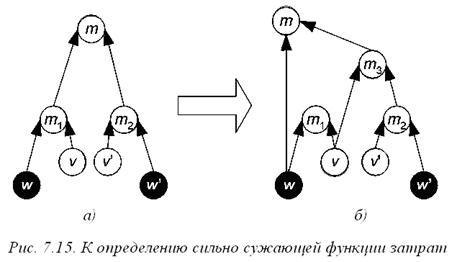
Определение 7.12 Сужающая функция затрат называется сильно сужающей, если для любых групп s ₁ и s₂ из двух или более исполнителей выполнено по крайней мере одно из двух условий:

1) для любого ;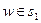

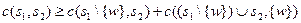2) для любого .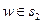

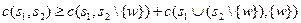Таким образом, для сильно сужающей функции затрат всегда можно, не увеличив затрат иерархии, проделать описанное выше преобразование. Это преобразование не может быть проделано только в том случае, если иерархия является последовательной иерархией, что приводит к следующему утверждению.

Утверждение 7.5 Для сильно сужающей функции затрат на множестве 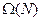существует оптимальная последовательная иерархия.

Следовательно, при сильно сужающей функции затрат оптимальную на 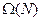иерархию можно искать только среди последовательных иерархий, для чего разработаны как аналитические методы, так и численные алгоритмы.

Несложно показать, что как монотонные по группам функции, так и функции, не являющиеся монотонными по группам, могут быть сужающими, могут быть расширяющими, могут не быть ни сужающими, ни расширяющими. Кроме того, в предельных случаях функция может быть и сужающей, и расширяющей одновременно.

В общем виде секционная функция затрат менеджера c (s ₁, …, s_r) представляет собой функцию множеств и потому является довольно сложным объектом. Задание такой функции затрат в общем случае сводится к прямому перечислению ее значений для всех возможных наборов групп, что обычно невозможно из-за огромного количества таких наборов.

Для иллюстрации свойств секционных функций представим функцию затрат менеджера в компактной форме, поставив в соответствие каждой группе или набору групп одну или несколько числовых характеристик и считая функцию затрат менеджера зависящей уже от этих характеристик.

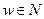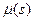Проще всего это сделать, введя меру на множестве исполнителей. Каждому исполнителю ставится в соответствие положительное число - его мера. Мерой группы исполнителей называется суммарная мера исполнителей, входящих в группу, то есть . Тогда считаем, что функцию затрат менеджера можно записать в виде функции r +1 переменных: 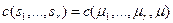, где 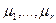- это меры групп, управляемых непосредственными подчиненными менеджера, а 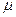- мера группы, которой управляет он сам. Такую функцию затрат будем называть зависящей от мер. Функция затрат менеджера задается для любого количества его непосредственных подчиненных r и симметрична по перестановке аргументов 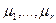(но не последнего аргумента 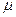).Содержательно мера исполнителя может соответствовать, например, сложности выполняемой им работы. Тогда мера группы соответствует суммарной сложности или объему работ, выполняемых группой, и именно от этой сложности зависят затраты по управлению группой.

Пример 7.4. Пусть все исполнители считаются одинаковыми, и каждый из них имеет меру, равную единице. Тогда мера группы равна количеству входящих в нее исполнителей, а функция затрат менеджера зависит от количества подчиненных ему исполнителей и от количества исполнителей, которыми управляют непосредственно подчиненные ему сотрудники.

Задание меры исполнителей, конечно, является далеко не единственным, хотя и самым простым способом введения числовых характеристик групп. В частности, выше рассматривались «потоковые» функции затрат менеджера, зависящие от материальных, финансовых и информационных потоков между подчиненными группами исполнителей. Приведем несколько примеров функций затрат, зависящих от мер.

Пример 7.5. Пусть затраты менеджера пропорциональны мере управляемой им группы, то есть 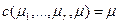. В этом случае среди всех возможных иерархий оптимальна веерная иерархия, поскольку любая иерархия по определению включает менеджера, управляющего группой N из всех исполнителей, и только в веерной иерархии этот менеджер будет единственным. Однако оптимальные иерархии будут уже не столь тривиальными, если ограничиться поиском только среди r -иерархий, где r> 1 - некоторое заданное число.

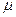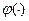Пример 7.6. Пусть функция затрат зависит от количества r непосредственных подчиненных менеджера и меры группы, которой управляет сам менеджер. Частным видом такой функции является мультипликативная функция затрат вида ,где и 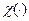- некоторые неотрицательные монотонно возрастающие функции.

В мультипликативной функции затраты по работе с непосредственными подчиненными 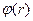умножаются на «коэффициент ответственности» 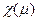, зависящий от меры управляемой менеджером группы.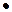

Пример 7.7. В некоторой литературе были введены и исследованы несколько более сложных зависящих от мер функций затрат менеджера:

(І)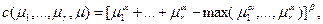

(ІІ)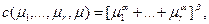

(ІІІ)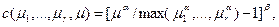

(IV)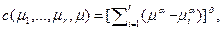

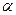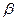Здесь и - некоторые неотрицательные параметры, позволяющие «подстроить» эти функции затрат к конкретным условиям. Ниже мы будем ссылаться на эти функции затрат по их номеру, то есть говорить о функции затрат (I), (II) и т.д.

Функции (I)-(IV) затрат менеджера определяются «сложностью» (объемом работ) сотрудников «секции» (отдела, подразделения и т.п.), которая непосредственно подчинена менеджеру. В различных организациях секция может управляться с использованием различных механизмов взаимодействия между менеджером и непосредственными подчиненными (внутри секции). Ниже функции (I)-(IV) интерпретируются как затраты менеджера для различных способов взаимодействия внутри секции. В менеджменте на качественном уровне рассматривается множество подобных способов взаимодействия.

Предположим, что среди непосредственных подчиненных менеджера имеется «полулидер», который полностью справляется со своими обязанностями, не требуя от непосредственного начальника затрат на управление собой. Этому случаю может соответствовать функция (I). В (I) затраты менеджера определяются сложностями групп, которые управляются всеми непосредственными подчиненными, кроме «полулидера». Под полулидером подразумевается подчиненный, который управляет группой с наибольшей сложностью. Если среди непосредственных подчиненных менеджера отсутствует «лидер», то менеджер несет затраты на управление всеми непосредственными подчиненными (функция (II)).

Предположим, что среди непосредственных подчиненных менеджера (внутри секции) имеется «лидер», который помогает решить проблемы взаимодействия других непосредственных подчиненных (например, с помощью своего авторитета или опыта). За счет этого снижаются затраты непосредственного начальника. Этому случаю может соответствовать функция затрат (III). Чем более сложной группой управляет подчиненный менеджеру лидер, тем выше значение «лидера», тем более снижаются затраты его начальника.

Функция (IV) может описывать затраты в процессе индивидуальной работы менеджера с каждым непосредственным подчиненным. Затраты определяются разностями между сложностью группы, которой управляет менеджер, и сложностями групп, которыми управляют непосредственные подчиненные.

Например, менеджер m, которому подчинена группа s_H (m), в процессеуправления непосредственным подчиненным m₁ передает ему информацию о той части группы s_H (m), которой m₁ не управляет. Объем этой информации определяется разностью сложностей и 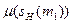. Сумма объемов информации по всем непосредственным подчиненным и определяет затраты менеджера (IV).

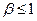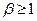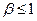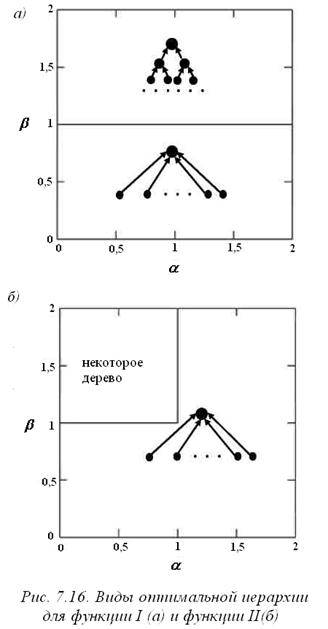
Очевидно, что функции (I) и (II) монотонны по группам, функции (III) и (IV) не являются монотонными по группам. Несложно проверить свойства сужения и расширения для этих функций. В результате можно доказать, что функция (I) при – расширяющая, а при - сужающая. Это значит, что при оптимальна веерная иерархия, а при 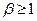оптимальным является некоторое 2-дерево (см. рисунок 7.16 a).

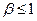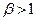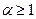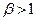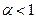Также доказывается, что функция (II) при расширяющая, а при и - расширяющая на непересекающихся группах, то есть в этих случаях оптимальна веерная иерархия (см. рисунок 7.16 б). В области и функция (II) не является ни расширяющей, ни сужающей даже на непересекающихся наборах групп. То есть для этого случая утверждение 7.5 не может помочь в поиске оптимальной иерархии. Однако функция (II) монотонна по группам, поэтому оптимальным является дерево (см. утверждение 7.3).

При 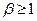функции (III) и (IV) сужающие, то есть оптимальной является 2-иерархия, имеющая минимальные затраты (см. утверждение 7.5). Для дерево с минимальными затратами можно найти с помощью алгоритмов. Однако это дерево может не быть оптимальной иерархией, поскольку функции (III) и (IV) не монотонны по группам.

Расширяющие и сужающие функции затрат приводят к оптимальности крайних случаев - веерной иерархии и 2-иерархии. Как правило, в реальных организациях имеет место «промежуточная» иерархия, в которой норма управляемости 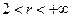. Поэтому функция затрат, описывающая такую организацию, не будет ни расширяющей, ни сужающей. Таким образом, важна разработка методов решения задачи об оптимальной иерархии для этого случая. На данный момент такие методы разработаны для важного класса так называемых однородных функций затрат.