Однородные функции затрат на управление

Определение 7.13. Функция затрат менеджера 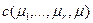, зависящая от мер, называется однородной, если существует такое неотрицательное число 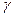, что для любого положительного числа A и любого набора мер 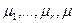выполняется тождество 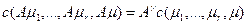. Число 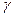называется степенью однородности функции затрат.

Таким образом, при однородной функции затрат пропорциональное увеличение мер групп всех исполнителей в A раз приводит к росту затрат менеджера в 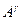раз.

Определение 7.14. r-мерным симплексом D_r называется такое множество r -мерных векторов x =(x ₁,…, x_r) с неотрицательными компонентами, что x ₁+…+ x_r =1. Элементы такого симплекса будем называть r - пропорциями или просто пропорциями.

Легко видеть, что если менеджер имеет r непосредственных подчиненных, то вектор 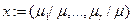является r -пропорцией. Будем в этом случае говорить, что менеджер делит подчиненную ему группу исполнителей между своими непосредственными подчиненными в пропорции x.

Для поиска оптимального дерева в случае функций затрат, зависящих от мер, существуют численные алгоритмы. Исследование результатов их работы при различных однородных функциях затрат позволяет выделить ряд общих свойств, которыми обладают оптимальные деревья, формализованных в определении 7.15.

Определение 7.15. Дерево называется (r, x)- однородным, если каждый его менеджер имеет ровно r непосредственных подчиненных и делит между ними подчиненную ему группу исполнителей в пропорции x =(x ₁,…, x_r). Число r называется нормой управляемости однородного дерева.

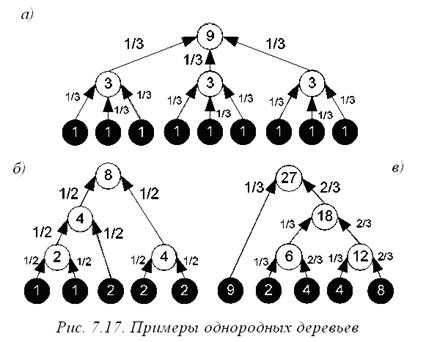
Пример 7.8. На рисунке 7.17 изображены три однородных дерева. Для каждого сотрудника на рисунке изображена мера управляемой им группы. Иерархия а) – это 3-дерево с пропорцией x =(1/3, 1/3, 1/3). Дерево имеет симметричный вид (однородные деревья всегда симметричны, если исполнители имеют одинаковые меры). Иерархия б) – это 2-дерево с пропорцией (1/2, 1/2), а иерархия в) – 2-дерево с пропорцией (1/3, 2/3).

В силу дискретности задачи для заданного множества исполнителей может не существовать ни одного однородного дерева (кроме веерной иерархии, которая всегда является однородной). В то же время, если однородное дерево существует, его затраты легко вычисляются.

Утверждение 7.6. Пусть заданы множество исполнителей N= {1,…, n } смерами 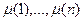и однородная степени 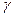функция затрат менеджера 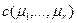. Если существует однородное дерево H с нормой управляемости r и пропорцией x= (x ₁, …, x_r), то его затраты определяются выражением:

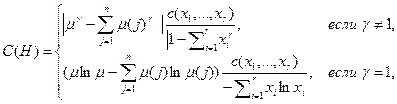(7.6)

где 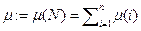– суммарная мера всех исполнителей.

Нижняя оценка затрат оптимального дерева. Имея аналитическое выражение для затрат однородного дерева, точно так же можно ставить вопрос о том, какое из всего множества однородных деревьев было бы оптимальным, если бы оно существовало. Для того чтобы найти такое наилучшее однородное дерево, необходимо минимизировать выражение (7.6) по всем возможным нормам управляемости r и пропорциям x. Соответственно, пара (r, x), на которой достигается этот минимум, даст параметры наилучшего однородного дерева, а, подставив их в формулу (7.6), получим его затраты.

Понятно, что при фиксированном множестве исполнителей N= {1,…, n } с мерами 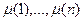топ-менеджер любого дерева будет иметь не более n непосредственных подчиненных, поэтому при поиске наилучшего однородного дерева минимизировать достаточно по всем r от 2 до n.

Кроме того, каждый непосредственный подчиненный топ-менеджера будет управлять, по меньшей мере, одним исполнителем, и, значит, мера управляемой им группы будет не меньше минимальной из мер исполнителей. Следовательно, каждая из компонент x_i, i= 1, …, r пропорции любого однородного дерева будет не меньше чем .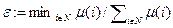

Для произвольного неотрицательного числа 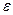обозначим через 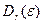ту часть симплекса D_r, на которой каждая компонента вектора больше или равна .

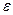Тогда при фиксированной функции затрат минимальные затраты однородного дерева определяются количеством n и мерами 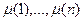исполнителей и задаются следующим выражением:

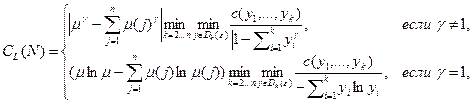(7.7)

где .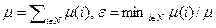

Поскольку 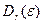– компактное множество, минимумы в формуле (7.7) достигаются при достаточно слабых условиях на функцию затрат (достаточно потребовать ее полунепрерывности снизу на симплексе), и ниже считается, что они достигаются.

Эмпирически установлено, что оптимальная (на множестве всех деревьев) древовидная иерархия «стремится» быть однородным деревом. В связи с этим возникает предположение о том, что, если для заданного множества исполнителей существует наилучшее однородное дерево (с нормой управляемости 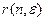и пропорцией 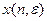), то оно и будет оптимальным на множестве всех деревьев. На самом деле оказывается, что справедлив даже более сильный результат.

Утверждение 7.7. Пусть заданы множество исполнителей N= {1,…, n } смерами 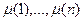и однородная степени 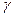функция затрат менеджера 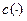. Тогда затраты оптимального дерева будут не меньше, чем C_L(N). Иначе говоря, функция C_L(N) является нижней оценкой затрат оптимального дерева.

Если ставится задача поиска оптимального r- дерева, то есть дерево, каждый из менеджеров которого имеет не более r подчиненных, то нижняя оценка его затрат будет определяться затратами наилучшего однородного r -дерева, то есть однородного дерева с нормой управляемости не более чем r.

Легко видеть, что затраты наилучшего однородного r -дерева задаются формулой:

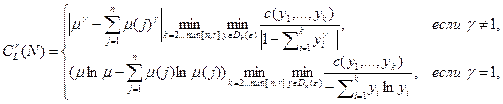(7.8)

Таким образом, справедливо следующее утверждение:

Утверждение 7.8. В условиях утверждения 7. 6 затраты оптимального r -дерева будут не менее C_L^r (N).

Описанная нижняя оценка затрат оптимального дерева имеет широкий спектр применения. Например, оказывается, что при большом количестве исполнителей она обычно достаточно точно аппроксимирует затраты оптимального дерева.