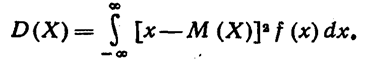 |
Среднее квадратическое отклонение непрерывной случайной величиныопределяется, как и для величины дискретной, равенством
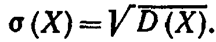 |
Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.
Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:
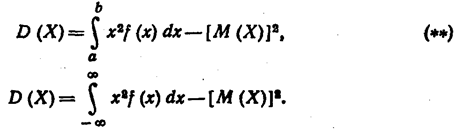 |
Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величин, которое описывается плотностью
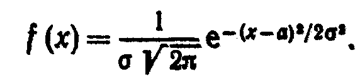 |
Мы видим, что нормальное распределение определяется двумя параметрами: a и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение.
Покажем, что вероятностный смысл этих параметров таков:
а есть математическое ожидание, σ—среднее квадратическое отклонение нормального распределения.
а) По определению математического ожидания непрерывной случайной величины,
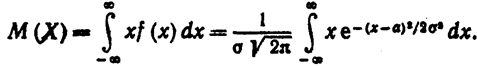
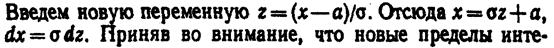
грирования равны старым, получим
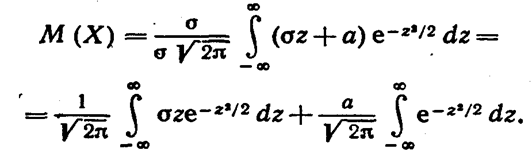
Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых
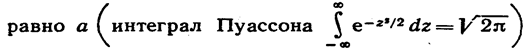
Итак, Μ (Χ) = a, т. е. математическое ожидание нормального распределения равно параметру а.
б) По определению дисперсии непрерывной случайной величины, учитывая, что Μ (Χ) = a, имеем
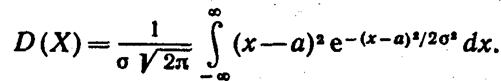
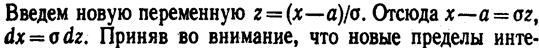
грирования равны старым, получим
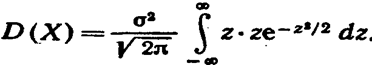
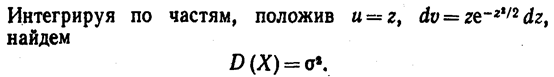
 Следовательно,
Следовательно,
Итак, среднее квадратическое отклонение нормального распределения равно параметру 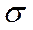
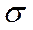
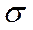 Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и (
Замечание 1. Общим называют нормальное распределение с произвольными параметрами а и ( > 0)
> 0)
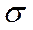 Нормированным называют нормальное распределение с параметрами а =0 и = 1.
Нормированным называют нормальное распределение с параметрами а =0 и = 1.
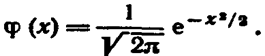 Плотность нормированного распределения
Плотность нормированного распределения
Эта функция табулирована.
Замечание 2.Функция F (х) общего нормального распределения
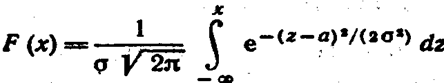 |
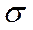 Где Z=(x-a)/
Где Z=(x-a)/
а функция нормированного распределения
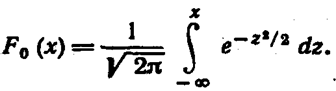 |
Функция f0 (х) табулирована. Легко проверить, что
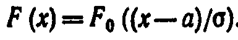 |
Замечание 3. Вероятность попадания нормированной нормальной величины Х в интервал (0, х) можно найти, пользуясь

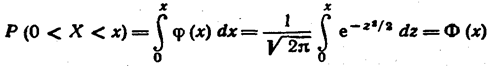
и, следовательно, в силу симметрии φ (x) относительно нуля
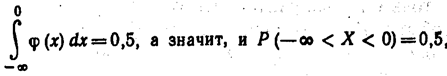 |
легко получить, что
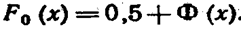
Действительно,
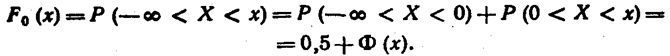 |
Нормальная кривая
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию
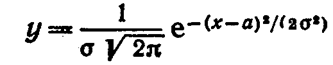 |
методами дифференциального исчисления.
1. Очевидно, функция определена на всей оси х.
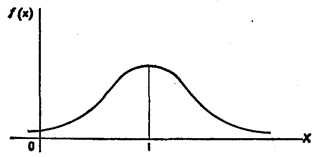 |
Рис. 1
2. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох.
3. Предел функции при неограниченном возрастании х
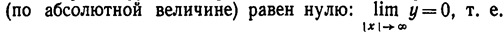 |
ось Ох служит горизонтальной асимптотой графика.
4. Исследуем функцию на экстремум. Найдем первую производную:
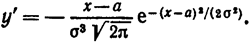
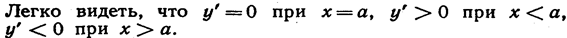
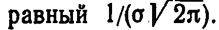 Следовательно, при х==а функция имеет максимум.
Следовательно, при х==а функция имеет максимум.
5. Разность х — а содержится в аналитическом выражении функции в квадрате, т.е. график функции симметричен относительно прямой х = а.
6. Исследуем функцию на точки перегиба. Найдем вторую производную:
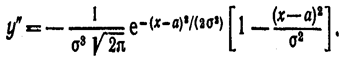
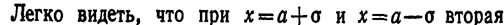
производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции
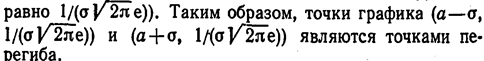
 На рис. 1 изображена нормальная кривая при а == 1
На рис. 1 изображена нормальная кривая при а == 1
Влияние параметров нормального
распределения на форму нормальной кривой
Выясним, как влияют на форму и расположение

ном направлении оси x на а единиц масштаба при а > О или в отрицательном направлении при а < 0, получим график f (χ—а). Отсюда следует, что изменение величины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает.
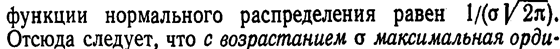 По-иному обстоит дело, если изменяется параметр σ (среднее квадратическое отклонение). Как было указано в предыдущем параграфе, максимум дифференциальной
По-иному обстоит дело, если изменяется параметр σ (среднее квадратическое отклонение). Как было указано в предыдущем параграфе, максимум дифференциальной
ната нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох: при
 |
вершинной·» и растягивается в положительном направлении оси Оу.
Подчеркнем, что при любых значениях параметров а и s площадь, ограниченная нормальной кривой и осью х, остается равной единице (см., второе свойство плотности распределения).
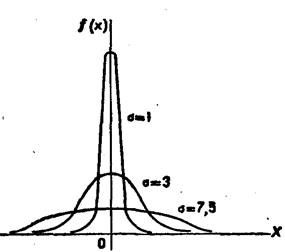
Рис.8.
На рис. 8 изображены нормальные кривые при различных значениях σ и а==0. Чертеж наглядно иллюстрирует, как изменение параметра σ сказывается на форме нормальной кривой.
Заметим, что при а = 0 и σ == 1 нормальную кривую
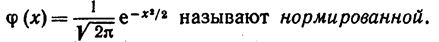
2. Вероятность попадания в заданный интервал нормальной случайной величины. Вычисление вероятности заданного отклонения.
Уже известно, что если случайная величина Χ задана плотностью распределения f (x), то вероятность того, что Χ примет значение, принадлежащее интервалу (α, β), такова:
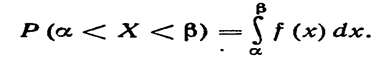
Пусть случайная величина Χ распределена по нормальному закону. Тогда вероятность того, что Χ примет значение, принадлежащее интервалу (α, β), равна
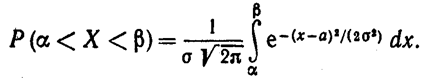
Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую пере-
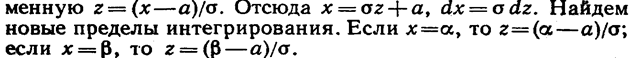
Таким образом, имеем
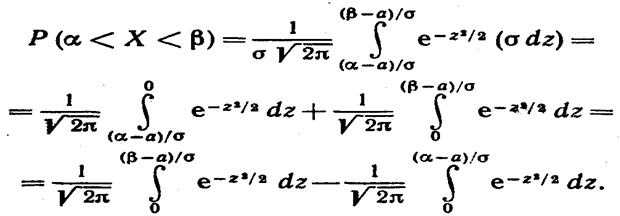
Пользуясь функцией Лапласа
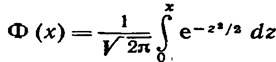
окончательно получим
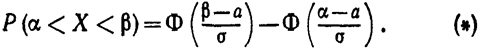 |
Пример. Случайная величина Χ распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Χ примет значение, принадлежащее интервалу (10, 50).
Решение. Воспользуемся формулой (*). По условию a=10
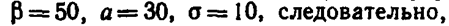
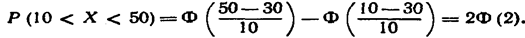
По таблице приложения 2 находим Φ (2) == 0,4772. Отсюда искомая вероятность

Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Χ по абсолютной величине меньше заданного положительного числа δ, τ. е. требуется найти вероятность
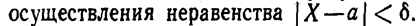
Заменим это неравенство равносильным ему двойным неравенством
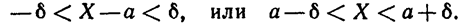
Пользуясь формулой (*) (см. § 5), получим
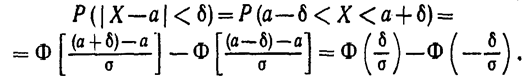
Приняв во внимание равенство
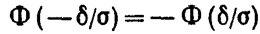
(функция Лапласа—нечетная), окончательно имеем
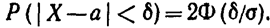
В частности, при а == О
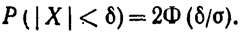
На рис. 3 наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (— δ, δ),
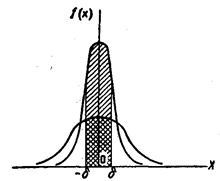
Рис.3.
больше у той величины, которая имеет меньшее значение σ.
Этот факт полностью соответствует вероятностному смыслу параметра σ
(σ есть среднее квадратическое отклонение; оно характеризует рассеяние
случайной величины вокруг ее математического ожидания).
Замечание. Очевидно, события, состоящие в осуществлении


Пример. Случайная величина Х распределена нормально. Математическое
ожидание и среднее квадратическое отклонение Χ соответственно равны
20 и 10.
Найти вероятность того, что отклонение по абсолютной величине будет
меньше
трех.
Решение. Воспользуемся формулой
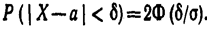

По таблице приложения 2 находим Φ (0,3) =0,1179. Искомая вероятность
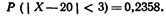
 2014-02-02
2014-02-02 550
550








