Принцип максимума

Классификация систем оптимального управления

Системы оптимального управления классифицируются по различным признакам. Рассмотрим некоторые из них.

По оптимизируемым показателям качества:

1) Оптимальные по быстродействию, обеспечивающие минимум функционала качеста

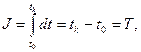
где Т – время протекания процесса управления при заданных ограничениях на управляющие воздействия. При этом перевод изображающей точки из одного положения в пространстве состояний в другое достигается за наименьшее время.

2) Оптимальные по расходу ресурсов, обеспечивающие минимум функционала качества

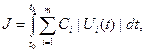
где С_i – коэффициент связи скорости расхода ресурсов с управляющими воздействиями. При этом перевод изображающей точки из начального состояния в конечное достигается при минимальных затратах ресурсов.

3) Оптимальные по затратам энергии, обеспечивающие минимум функционала

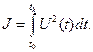
Кроме перечисленных, применяются оптимальные системы с минимальными потерями управления, характеризуемые минимальным отклонением действительных координат объекта от желаемых значений (следящие системы с минимальными ошибками воспроизведения задающего воздействия), оптимальные системы с максимальной производительностью и другие.

По характеру используемой информации:

1) Системы с полной априорной информацией об объекте управления.

В этом случае управляющие воздействия вырабатываются путем решения детерминированной задачи отыскания экстремума функционала.

2) Системы с неполной априорной информацией и пассивным ее накоплением.

В таких системах для выработки управляющего воздействия используются статистические методы обработки информации о работе системы.

3) Системы с неполной априорной информацией и активным ее накоплением в процессе работы.

В таких системах недостающая информация восполняется за счет использования пробных воздействий. Оптимальное управляющее воздействие вырабатывается с учетом реакции системы на пробные воздействия. Такие системы называют еще экстремальными системами.

Основными методами решения задач оптимального управления являются классическое вариационное исчисление; принцип максимума; метод динамического программирования.

Метод позволяет решать достаточно общие задачи нахождения оптимального времени переходного процесса, а также вычислять некоторые другие критерии оптимальности для непрерывных систем.

Проблема в общем виде содержит ряд достаточно сложных положений, однако для решения определенного класса задач об оптимизации, использование принципа максимума (называемого принципом максимума Понтрягина) дает инженерно приемлемый математический аппарат.

Пусть заданная система управления имеет вид, приведенный на рис.12.1.

На рисунке обозначено: ОУ – объект управления, УПИ - устройство получения информации, УПОИ – устройство передачи и обработки информации, УУ – управляющее устройство.

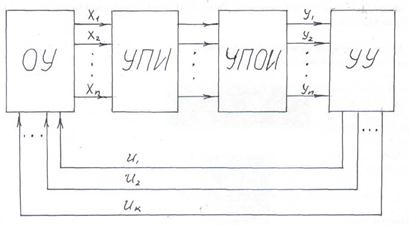
Рис.12.1. Блок-схема САУ

Управляющие воздействия U₁, U₂,….U_k, поступающие на объект управления, обеспечивают в каждый момент времени на выходе объекта параметры х₁,х₂,….х_n, которые характеризуют состояние объекта управления. Управляющие воздействия U_k, очевидно, в реальных условиях ограничены по своим значениям рядом условий. Если эти сигналы управления представить в виде векторов, направляемых по «К» координатным осям К – мерного пространства, то наложенные на них ограничения выделят в этом пространстве некоторую ограниченную замкнутую область, называемую областью управления Г_к. Совокупность всех векторов управляющих сигналов в каждый момент времени можно представить как суммарный вектор 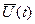с компонентами u₁(t), u₂(t),…u_k(t), определенный на отрезке времени t₀ £ t £ t₁ и расположенный внутри области управления. Вектор-функция 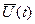, удовлетворяющая некоторым наложенным на нее условиям управления, определяется как допустимое управление. Заданными условиями управления могут быть кусочная непрерывность функции 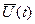, кусочная дифференцируемость и некоторые другие условия.

Если принять, что управляющее устройство в системе безинерционно, а функция управления 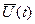кусочно-непрерывна, то ее значения могут, очевидно, без задержки во времени перемещаться из одной точки управления в любую другую.

Предполагается, что уравнения элементов, определяющих поведение объекта управления, представляют собой совокупность дифференциальных уравнений первого порядка (или уравнений, могущих быть приведенными к этому виду), имеющих следующий вид:

dx₁/dt = f₁(x₁,x₂,…x_n, u₁,….u_k),

……………………………….. (12.1)

dx_i/dt = f₁(x₁,x₂,…x_n, u₁,….u_k),

где i = 1,2,……n

здесь в соответствии с рис.12.1 величины x₁,x₂,…x_n –выходные параметры объекта; u₁,u₂,….u_k – входные (управляющие) воздействия.

Перейдя к векторной форме, примем:

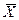- вектор с компонентами x₁,x₂,…x_n; 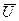- вектор с компонентами u₁,u₂,….u_k; 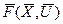- вектор с компонентами .

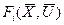При этом вектор-функции F_i в (12.1) считаются непрерывными функциями аргументов 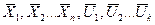и непрерывно дифференцируемыми по этим аргументам. Поэтому уравнение (12.1) можно записать в векторной форме

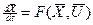. (12.2)

Уравнение (12.2), как и уравнение (12.1) можно рассматривать как уравнение элементов, определяющих поведение объекта управления с «К» регулируемыми органами. Такая система при безинерционном управляющем устройстве, является «К» - мерной системой управления.

Для обеспечения оптимального закона управления необходимо найти все значения U_i как функции всех выходных параметров х_i и всех других К – 1 управляющих воздействий u_i или, иначе говоря, определить функции:

U₁ = j₁(x₁,x₂,…x_n, u₂,u₃….u_k)

U₂ = j₁(x₁,x₂,…x_n, u₁,u₃….u_k)

………………………………

U_k = j₁(x₁,x₂,…x_n, u₁,u₂….u_k-1)

или в векторной форме

.

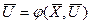Если сигналы управления с учетом определенных ограничений заданы, т.е. 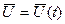известны и вектор 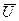находится внутри или на границе К – мерного пространства, то решение уравнения (12.2) при любых начальных условиях однозначно определяет выходную вектор-функцию 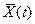. Выбранный допустимый закон управления 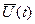при t_o £ t £ t₁, изображающую точку 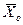, определяющую состояние объекта управления в момент времени t_o и в n – мерном пространстве имеющую координаты 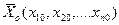, переводит в положение с координатами 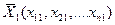, что и является целью управления.

Если задаться в соответствии с (12.2) функцией 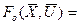F_o(x₁,x₂,…x_n, u₁,u₂….u_k) и считать целью управления указанный выше перевод изображающей точки в фазовом пространстве из состояния 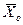в состояние 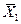, то требуется найти такую вектор-функцию управления 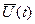с учетом заданных ограничений, которая обращала бы в минимум или максимум функционал вида

.

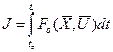Если принять, что 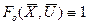, то это приводит к J = t₁ - t_o, что означает минимальное время перехода изображающей точки в фазовом пространстве из состояния 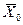в состояние 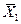, т.е. максимально возможное быстродействие системы.

Решение поставленной задачи с использованием принципа максимума сводится к следующему.

Дополним основную систему уравнений (12.1) системой уравнений относительно дополнительных переменных y_о,y₁,…y_n в виде

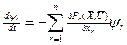, (12.3)

где i = 0,1,…n

Системы уравнений (12.1) и (12.3) объединяются одной записью при введении вспомогательной функции H переменных x_i, y_i и u_j, (i = 0,1,….n; j = 1,2,….k), называемой гамильтонианом. Эта функция называется также функцией Понтрягина.

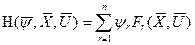. Тогда

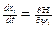, (12.4)

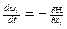, (12.5)

где i= 0,1,….n

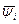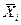При выбранных значения и функция Н зависит только от управляющего воздействия .

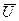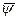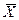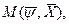Если считать, что максимальное значение непрерывной функции Н в некоторой точке области управления при выбранном значении и равно то = .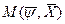

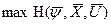Принцип максимума формулируется следующим образом. Для оптимальности управления 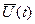и траектории 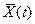необходимо существование такой ненулевой непрерывной вектор-функции 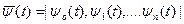,соответствующей функциям 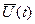и 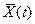, что:

1) при любом t на отрезке t_o £ t £ t_k функция 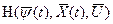переменного 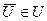достигает в точке 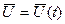максимума;

2) в конечный момент времени t_k выполняются соотношения

y_о(t_k) £ 0, .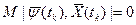

Кроме того, если величины 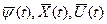удовлетворяют системе уравнений (12.4) и (12.5) и условию п.1, то функции y_о(t) и 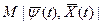переменного t являются постоянными, и условие п.2 выполняется в любой момент времени на отрезке t_o £ t £ t_k.

Если критерием оптимальности является максимальное быстродействие, то целью расчета является определение вектор-функции 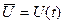, при которой перемещение системы из состояния М_о в состояние М_k в многомерном пространстве происходит за минимальное время (рис.12.2).

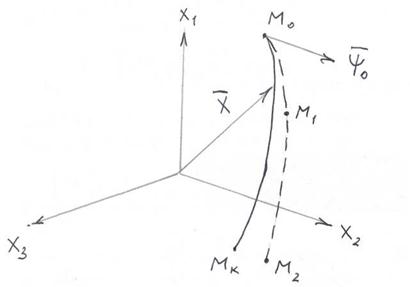Рис.12.2. Переход изображающей точки из начального положения в конечное

Принцип максимума сводится к подбору в каждой данной точке многомерного пространства вектора 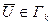так, чтобы функция 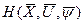стала максимальной.

Зная вектор 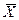в точке М_о (рис.12.2), можно определить в этой точке вектор 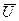и затем переместиться в ближайшую точку М₁, где снова определить значение 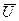и т.д.

В итоге кривая М_оМ₁М₂… в многомерном пространстве будет экстремалью, т.е. перемещение системы по этой кривой происходит с максимальным быстродействием. Если экстремаль не проходит через требуемую точку М_к, то следует изменить начальный вектор 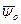. В этом случае получится группа экстремальных кривых, одна из которых при соответствующем подборе вектора 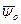пройдет через требуемую точку М_к.