Из школьного курса математического анализа известно, что для функции одной переменной 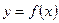 , которая определена и непрерывна в области D,
, которая определена и непрерывна в области D,
приращении функции есть разность
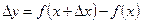 ,
,
где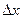 - приращение аргумента.
- приращение аргумента.
Рассмотрим функцию нескольких переменных
u = f(M) или
u=f(х, у,…z),
которая определена и непрерывна в области D.
Для таких функций введем понятия полного и частного приращений функций. Пусть первая координата х точки М получает приращение 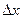 и становится равной
и становится равной 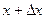 . Другие координаты точки М (аргументы данной функции), остаются без изменения. Точка М(х, у,…z) преобразована в точку
. Другие координаты точки М (аргументы данной функции), остаются без изменения. Точка М(х, у,…z) преобразована в точку
М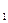 (х +
(х +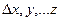 ), функция при этом изменила свое значение на величину
), функция при этом изменила свое значение на величину
f (М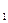 ) – f (М) =
) – f (М) = 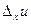 или
или
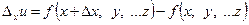 ,
,
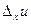 называется частным приращениемфункции f по х.
называется частным приращениемфункции f по х.
Аналогично можно определить частные приращения по другим переменным:
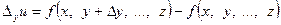 - частное приращение функции f по y,
- частное приращение функции f по y,
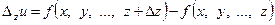 - частное приращение функции f по z.
- частное приращение функции f по z.
Полным приращениемфункции u=f(х, у,…z) называется
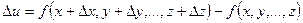 .
.
Если существует конечный или бесконечный предел отношения частного приращения функции 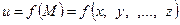 по одной из независимых переменных к приращению этой независимой переменной при условии, что последнее приращение стремится к нулю произвольным образом, то он называется частной производной данной функции по соответствующей независимой переменной в точке
по одной из независимых переменных к приращению этой независимой переменной при условии, что последнее приращение стремится к нулю произвольным образом, то он называется частной производной данной функции по соответствующей независимой переменной в точке 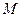 , обозначают:
, обозначают:
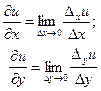
Если функция 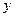 зависит от одного аргумента:
зависит от одного аргумента: 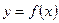 , то, как известно, ограничиваются термином «производная функции»,обозначают
, то, как известно, ограничиваются термином «производная функции»,обозначают
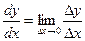 .
.
Также встречается следующие обозначения производных:
ü для функции одной переменной y = f(x) производную обозначают
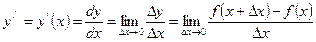
ü в случае функции двух переменных z = f(x, y) обозначают
частную производную функции f (x,y) по х:
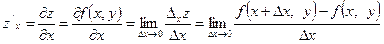
частную производную функции f (x,y) по y:
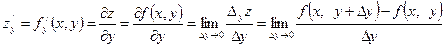 .
.
 2014-02-02
2014-02-02 798
798








