Свойства дифференциалов
1) если С – постоянная величина, то dC= 0;
2) 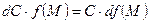 , т.е. постоянный множитель можно выносить за знак дифференциала;
, т.е. постоянный множитель можно выносить за знак дифференциала;
3) 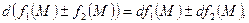
4) 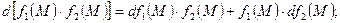
5) 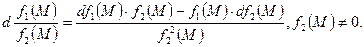
Теорема Ферма. Если функция y=f(x) непрерывна в (а, b), имеет экстремум - max (min) в некоторой внутренней точке 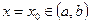 и дифференцируема в этой точке, то ее производная в этой точке равна нулю:
и дифференцируема в этой точке, то ее производная в этой точке равна нулю:
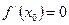 .
.
Теорема Роля. Если функция y=f(x) непрерывна на отрезке [a, b], дифференцируема на (a, b) и имеет на концах отрезка равные значения f(a) = f(b)=c, то на интервале (a, b) существует хотя бы одна точка х = х0 такая, что f /(x0) =0
Действительно. Так как функция непрерывна на [a, b], то, по теореме Вейерштрасса (2.1.13) она имеет на этом отрезке наименьшее и наибольшее значения: m и М.
· Если m= М, то f /(x0)- const и для любого 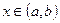 имеем f /(x0) =0.
имеем f /(x0) =0.
· Если 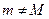 , то хотя бы одно из этих значений соответствует внутренней точке
, то хотя бы одно из этих значений соответствует внутренней точке 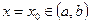 , но тогда по теореме Ферма имеем f /(x0) =0.
, но тогда по теореме Ферма имеем f /(x0) =0.
Геометрический смысл теоремы Роля состоит в том, что существует хотя бы одна точка (x0 , f(x0)) такая, касательная в которой к графику функции y=f(x) будет параллельна оси Ох.
Теорема Коши. Если функция 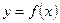 и
и 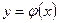 непрерывны на [a, b], дифференцируемы на (a, b), причем
непрерывны на [a, b], дифференцируемы на (a, b), причем 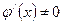 , то существует хотя бы одна точка
, то существует хотя бы одна точка 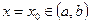 , такая, что
, такая, что 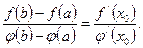
Теорема Лагранжа. Если y=f(x) непрерывна на [a, b], дифференцируема на (a, b), то существует хотя бы одна точка 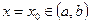 такая, что
такая, что 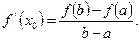 .
.
Теорема Лопиталя. Пусть функции y=f(x) и 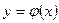 в окрестности точки х= а непрерывны, дифференцируемы и
в окрестности точки х= а непрерывны, дифференцируемы и 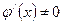 . При этом при
. При этом при 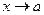 или
или 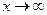 одновременно
одновременно 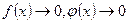 или
или 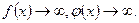
Тогда, если существует 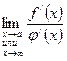 , то также существует
, то также существует 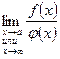 , причем
, причем 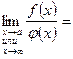
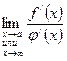 .
.
 2014-02-02
2014-02-02 433
433








