Рассмотрим следующие виды монотонных функций. Очевидно, что если
1) x1<x2 y1<y2, тогда y=f (x)- возрастающая функция,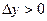 ;
;
2) x1<x2 y1>y2 тогда y=f(x) – убывающая функция, 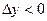 ;
;
3) x1<x2, 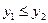 , тогда y=f3(x) – неубывающая функция, в этом случае существует отрезок [a, b], для которого у сохраняет постоянное значение,
, тогда y=f3(x) – неубывающая функция, в этом случае существует отрезок [a, b], для которого у сохраняет постоянное значение, 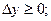
4) x1<x2, 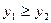 y=f (x) – невозрастающая функция, существует
y=f (x) – невозрастающая функция, существует
определенный отрезок [c, d], для точек которого у является постоянным,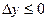 .
.
Необходимые условия монотонности функции:
1)если функция y=f(x) возрастает на (a, b), то f /(x)>0 для 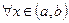 ;
;
2) если y=f(x) - неубывающая функция на (a, b), то 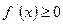 для
для 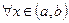 ;
;
3)если функция y=f(x) убывает на (a, b), то 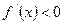 для
для 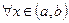 ;
;
4) если функция y=f(x) является невозрастающей на (a, b), то 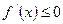 для
для 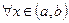 .
.
 2014-02-02
2014-02-02 331
331








