До сих пор мы молчаливо предполагали, что во время движения орты постоянны и дифференцировать их по времени нет необходимости. Это предположение справедливо не всегда. Например. Оно не справедливо, если происходит криволинейное движение. Простейший случай такого движения – движение по окружности или, в более общем случае – по плоской кривой. Кривая называется плоской, если все её точки лежат в одной плоскости (см. рис. 1). Как легко заметить, орты координат при этом изменяют своё направление, то есть зависят от времени.
В случае вращения по окружности с постоянной по модулю скоростью известно, что на материальную точку действует центростремительная сила
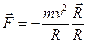 ,
,
где 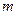 – масса материальной точки,
– масса материальной точки, 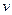 – модуль её скорости,
– модуль её скорости, 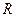 – радиус окружности,
– радиус окружности, 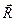 – радиус-вектор, проведенный из центра окружности в ту точку, где в данный момент находится материальная точка. Знак минус указывает, что действующая на материальную точку сила направлена к центру окружности.
– радиус-вектор, проведенный из центра окружности в ту точку, где в данный момент находится материальная точка. Знак минус указывает, что действующая на материальную точку сила направлена к центру окружности.
При движении по плоской кривой формулу для центростремительной силы можно обобщить. Для этого надо сделать несколько шагов.
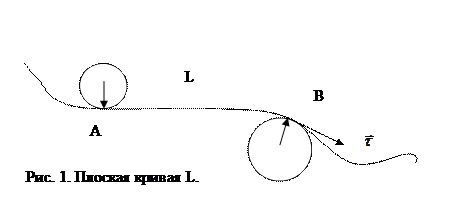
Выделим на плоской кривой L произвольные точки A и B. Построим окружности, касающиеся этих точек; стрелки указывают радиусы 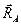 и
и 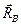 , проведенные из центров окружностей в точки касания. Соответствующие радиусы (не векторы) называются радиусами кривизны в точках
, проведенные из центров окружностей в точки касания. Соответствующие радиусы (не векторы) называются радиусами кривизны в точках 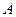 и
и 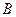 . Обратная величина, например,
. Обратная величина, например, 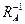 , называется кривизной кривой L в точке
, называется кривизной кривой L в точке 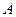 . Кривая должно быть плавной. В точке излома (в физике таких кривых не бывает) кривизна не определена. Для прямой линии кривизна стремится к нулю (радиус кривизны бесконечен). В точке
. Кривая должно быть плавной. В точке излома (в физике таких кривых не бывает) кривизна не определена. Для прямой линии кривизна стремится к нулю (радиус кривизны бесконечен). В точке 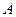 кривизна считается положительной, в точке
кривизна считается положительной, в точке 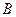 – отрицательной.
– отрицательной.
Если точка движется со скоростями 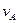 и
и 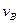 , то на неё действуют центростремительные силы
, то на неё действуют центростремительные силы 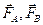 , определяемые указанной формулой. Это, в частности, означает, что они движутся с центростремительным ускорением
, определяемые указанной формулой. Это, в частности, означает, что они движутся с центростремительным ускорением
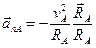 или
или 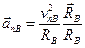 .
.
Но это не полное ускорение материальной точки. Для того, чтобы найти полное ускорение учтем, что при движении по плоской кривой скорость имеет вид
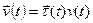 ,
,
где 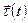 – вектор, касательный к рассматриваемой точке (например, к точке В, см. рис. 1), причем он зависит от времени,
– вектор, касательный к рассматриваемой точке (например, к точке В, см. рис. 1), причем он зависит от времени, 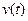 - модуль скорости в этой точке.
- модуль скорости в этой точке.
Чтобы найти ускорение надо продифференцировать скорость:
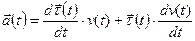 .
.
Первое слагаемое называется тангенциальным (касательным) ускорением,
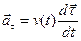 ,
,
и учитывает поворот касательного орта (для движения по прямой тангенциальное ускорение равно нулю), второе слагаемое – центростремительное ускорение,
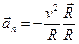 ,
,
и учитывает изменение модуля скорости.
Таким образом, полное ускорение равно
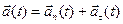 ,
,
а так как радиус, проведенный в точку касания перпендикулярен касательной, модуль полного ускорения равен
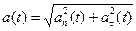 .
.
 2014-02-02
2014-02-02 1971
1971
