Моделирование обслуживающих аппаратов

В качестве математической модели обслуживающего аппарата, также как и для потоков, можно использовать вероятность состояния (обслуживающих аппаратов и очередей) в любой момент времени. Доказано, что если входные потоки простейшие, то для математического описания обслуживающих аппаратов можно использовать теорию марковских процессов. Под марковским процессом понимается последовательность смены состояний системы. Вероятность каждого из состояний не зависит от того, из какого состояния система перешла в искомое состояние, а определяется вероятностью настоящего состояния и вероятностью перехода. В марковском процессе фигурируют два независимых события:

1) система находится в настоящий момент в конкретном состоянии;

2) под воздействием управления (известных интенсивностей перехода) система перейдёт (или не перейдет) в другое состояние.

Следовательно, для того чтобы система перешла в следующее состояние необходимо, чтобы состоялись два выше рассмотренных события.

Допустим, под воздействием входного потока и потока обслуживания система может переходить из состояния S₀ (начальное состояние), через промежуточные состояния S₁, S₂, …, в S_n (конечное состояние). Для вероятного описания этих состояний, необходимо найти, в общем случае, вероятность перехода системы из S_i в S_j за время t (p_ij(t)). Если принять, что в момент времени t₀ (в прошлом) система находилась в состоянии S_i, а к моменту времени t (настоящее время) система находится в состоянии S_r, и под воздействием управляющих потоков (входного потока и обслуживания) в момент времени 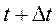(будущее) система перейдет в состояние S_j, то в соответствии с формулой Маркова (модель марковского процесса) вероятность перехода системы из i-го состояния в j-ое, за время от t₀ до 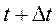определится из уравнения

,

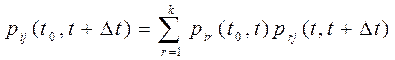где p_ir(t₀, t) определяет вероятность перехода системы к моменту времени t из состояния S_i в промежуточное S_r или вероятность нахождения системы на момент времени t в состоянии S_r; p_rj (t, t+Dt) определяет вероятность перехода системы к моменту времени t+Dt под воздействием управления из промежуточного состояния S_r в конечное искомое состояние S_j. На основании выше изложенного можно считать, что уравнение Маркова есть аналитическая модель системы обслуживания.

Как правило, при описании системы задаются значения вероятности начального состояния системы (выполнение первого события Марковского процесса) и вероятности (интенсивности) одношагового перехода системы из одного состояния в другое (второе событие). Поэтому, зная вероятности исходного состояния системы, можно определить вероятности состояний на последующих шагах.

Для описания динамики поведения системы обслуживания Колмогоровым на основе уравнения Маркова была предложена система дифференциальных уравнений вероятностей состояния системы. Допустим, что система находится в состоянии S_i. Известны интенсивности перехода из состояния S_i в возможные состояния S_j l_ij(t), которые полностью определяют вероятности одношагового перехода. Тогда граф примерной системы будет примет вид рис. 4.

lii

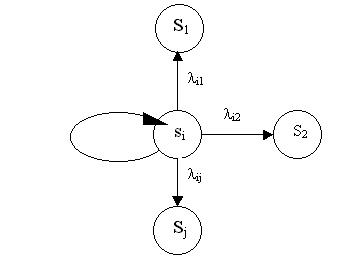
Рис. 4

Пользуясь уравнением Маркова, Колмогоров составил систему дифференциальных уравнений (аналитическую модель системы обслуживания) вида

.

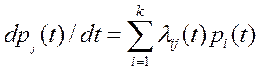Как правило, в момент времени t=0 известны: p_i(0) и l_ij(0).

Решением дифференциальных уравнений являются вероятности состояний объекта, которые полностью определяют характеристики системы обслуживания.

Методика составления дифференциальных уравнений Колмогорова. Уравнения Колмогорова составляются в следующей последовательности.

1.Задаются возможные состояния системы (допустим s₁, s₂, s₃, s₄).

2.Задаются интенсивности переходов из s_i состояния в состояние s_i l_ij.

3.Строится граф системы, вершинами которого являются состояния, дугами - интенсивности переходов. В рассматриваемом случае граф может иметь вид рис. 5.

l₄₁

l₁₄

l₄₃ l₄₂

l₃₄ l₂₄ l₂₁

l₃₂

Рис. 5

4. Составляется система дифференциальных уравнений. Число уравнений соответствует числу состояний системы. Допустим, необходимо записать уравнение для состояния s_i. Запись ведется с использованием мнемонического правила в следующей последовательности. В левой части уравнения записывается 1-я производная вероятности состояния s_i dp_i(t)/dt. В правой части уравнения записывается алгебраическая сумма произведений интенсивности перехода и вероятности состояния системы. При этом произведение положительно, если система входит в описываемое состояние и отрицательно, если система выходит из этого состояния.

В рассматриваемом примере уравнение для состояния s₄ примет вид

.

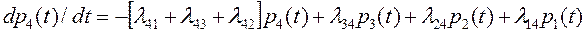Для того чтобы исключить нулевые решения системы, необходимо вместо одного из уравнений записать .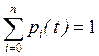

Если необходимо определить вероятности состояний системы в установившемся режиме (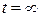), то систему дифференциальных уравнений приводят к системе линейных алгебраических уравнений.

Зная вероятности системы, как результат решения системы дифференциальных уравнений, можно определить различные характеристики системы обслуживания.

Пример решения системы в графическом виде показан на рис.6, где 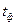- финальное время, при котором все вероятности системы придут к своим установившимся (финальным) значениям, а система дифференциальных уравнений сведется к системе алгебраических уравнений

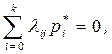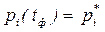где - финальная вероятность.

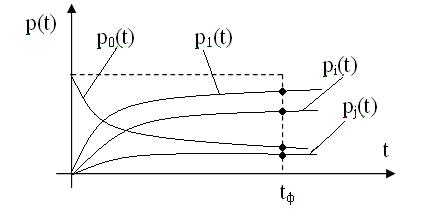
Рис. 6