Допустим, что в примере со студенческим ВЦ, рассмотренном ранее, входной поток и обслуживание простейшие (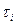 ,
,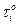 – подчиняются показательному закону соответственно с м.о.=9,6 и с м.о.=8).
– подчиняются показательному закону соответственно с м.о.=9,6 и с м.о.=8).
В этом случае модель ВЦ в виде системы дифференциальных управлений Колмогорова будет определена следующим образом.
1. Возможные состояния ВЦ:
S0 – ВЦ свободен; S1 – в ВЦ один студент и он обслуживается; S2 - в ВЦ два студента один обслуживается, один стоит в очереди; S3 – в ВЦ три студента один обслуживается, два стоят в очереди; аналогично определяется S4; S5 – ВЦ полностью занят.
2. Интенсивности переходов.
Поскольку в ЭВМ1 на обслуживание поступает только 25% студентов (см. пример в п.1), следовательно, интенсивности, с которыми осуществляются переходы в состояния S1, S2 … S5, определятся следующим образом:
1)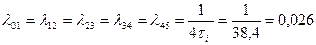 [студента в мин.];
[студента в мин.];
2)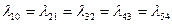 численно равны интенсивности обслуживания ЭВМ1
численно равны интенсивности обслуживания ЭВМ1 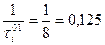 [студента в мин.].
[студента в мин.].
3. Граф ВЦ примет вид
l 01 l12 l23 l34 l45
01 l12 l23 l34 l45
l10 l21 l32 l43 l54
4. Система дифференциальных уравнений (аналитическая модель ВЦ) имеет вид
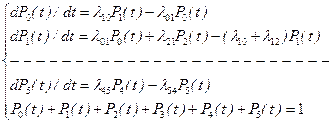
Решая систему, получим значения 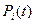 .
.
5. Искомый коэффициент загрузки ЭВМ1 определится по формуле К3(t)=1-Р0(t).
 2014-02-02
2014-02-02 753
753








