Кронекерово произведение

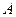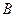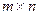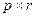Определение 6.3Пусть и - прямоугольные матрицы соответственно размеров и . Кронекеровым произведением 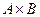называется матрица 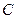размеров 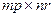следующего блочного строения .

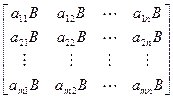Приведем основные свойства кронекерова произведения матриц.

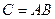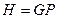Свойство 6.2. Пусть и , тогда .

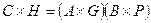Доказательство следует из правила блочного произведения матриц.

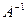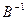Свойство 6.3. Пусть существуют и , тогда .

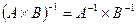Доказательство. По доказанному ранее (Свойство 6.2), имеем 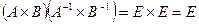. Из полученного равенства вытекает требуемое утверждение.

Свойство 6.4. .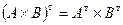

Доказательство следует из определения операций кронекерова произведения и транспонирования матриц.

Свойство 6.5. Пусть 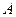- квадратная матрица порядк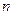а , а 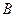- квадратная матрица порядка 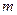, тогда .

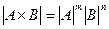Доказательство. Если матрица A имеет верхний треугольный вид, то утверждение получается последовательным разложением определителя по теореме Лапласа по первым m столбцам. Если матрица A имеет нижний треугольный вид, то утверждение получается последовательным разложением определителя по теореме Лапласа по первым m строкам. Рассмотрим случай, когда матрица A не треугольная. Элементарными преобразованиями со строками (а именно, подстановкой строк и прибавлением к одной строки, другой строки умноженной на число) приведём матрицу A к треугольному виду T. Тогда 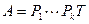, где 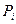- матрица элементарных преобразований. Имеет место равенство 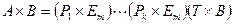, из которого выводим 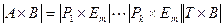. Поскольку T – треугольная матрица, то 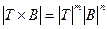. Матрица элементарного преобразования 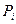, если она соответствует прибавлению к некоторой строке другой строки, умноженной на число, имеет треугольный вид, и, значит 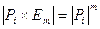. Если матрица элементарного преобразования 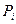соответствует подстановке двух строк, то 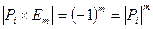. Таким образом, 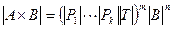. Для доказательства утверждения осталось заметить равенство .

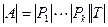Следствие 6.2. .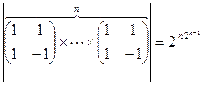

Доказательство проведём индукцией по n. Положим 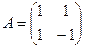и 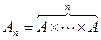. При n=2 имеем 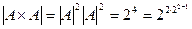, т.е. утверждение верно. Пусть оно справедливо при n-1. Тогда 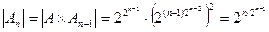, что и требовалось доказать.