Скорость точки в криволинейном движении

Скорость точки в криволинейном движении представляет собой векторную величину, характеризующую для каждого данного момента быстроту движения точки и направление этого движения.

Пусть точка М описывает данную криволинейную траекторию, двигаясь по закону , где дуговая координата этой точки (рис.11.3)

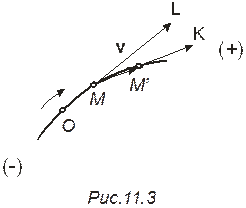
Пусть в момент времени t движущаяся точка занимает положение М на траектории. Пусть через малый промежуток времени Δt (в момент t+ Δt) та же точка занимает положение М'. Тогда или .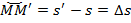

Вектор 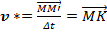.При приближении Δt к нулю, в пределе направление вектора 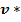совпадает с направлением касательной к траектории в точке М, а модуль его будет равен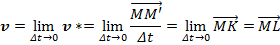

Для модуля скорости имеем:

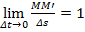, следовательно, .

Построим вектор 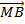, равный отношению изменения скорости 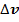к соответствующему промежутку времени Δt:

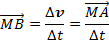
Этот вектор называется средним ускорением точки за время Δt.

Так как при делении вектора 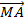на положительную скалярную величину Δt его направление не изменяется, то направление среднего ускорения 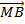совпадает с направлением вектора .

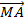Предел, к которому стремится среднее ускорение при Δt→0, называется ускорением точки в данный момент t. Мы будем обозначать ускорение через .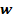

Следовательно, .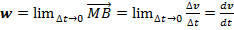

Пусть на рис.11.5 а вектор 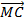есть вектор, к которому стремится в пределе при 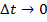среднее ускорение 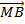, тогда .

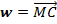Если проведем из какой-нибудь неподвижной точки О векторы 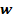точки М параллельно касательной к годографу скорости в соответствующей точке m.