Показатель в форме средней величины выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Сущность среднейвеличины заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
Задачи, которые решаются с помощью средних показателей:
1) характеристика уровня развития явления (средний балл группы);
2) сравнение нескольких уровней (сравнение средней заработной платы работников двух предприятий);
3) характеристика изменения уровня явления во времени (успеваемость по годам);
4) средние величины используются в планировании и прогнозировании.
Теория и практика выработала ряд требований, которые предъявляются к вычислению средних показателей:
1. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.
2. Если совокупность неоднородна, то общая средняя должна быть заменена или дополнена групповыми средними, т. е. средними, рассчитанными по качественно однородным группам.
3. Чтобы средняя отражала то общее, что характерно для всей совокупности, ее необходимо исчислять для всей массы изучаемых фактов.
Выделяют два класса средних величин:
1) Степенные средние:
– средняя геометрическая;
– средняя квадратическая и др.
– мода;
– медиана;
– квартили;
– перцентили;
– децили и др.
Средние степенные
В случае, когда каждый из вариантов признака встречается только один раз, средняя называется простой, если варианты признака повторяются различное число раз, то средняя называется взвешенной и ее расчет производится по сгруппированным данным или вариационным рядам.
Все перечисленные средние степенные величины объединяются в общей формуле средней степенной при различных значениях показателя степени.
Таблица 5.1
Виды средних степенных
| Вид средней | Простая средняя | Взвешенная средняя |
1. Степенная 2. Гармоническая 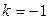 3. Геометрическая 3. Геометрическая  4. Арифметическая 4. Арифметическая 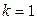 5. Квадратическая 5. Квадратическая 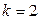 | 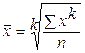 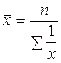 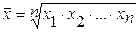 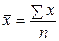  | 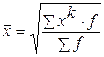 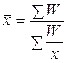 , где , где 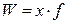 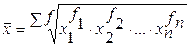 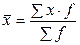 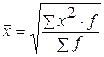 |
где 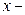 варианты признака;
варианты признака;
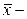 среднее значение признака;
среднее значение признака;
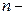 число вариантов признака,
число вариантов признака, 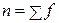 ;
;
 частоты;
частоты;
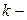 показатель степени.
показатель степени.
При использовании одних и тех же исходных данных чем больше k в формуле средней степенной, тем больше значение средней величины:
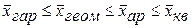 .
.
Это свойство степенных средних возрастать с показателем степени определяющей функции называется в статистике правилом мажорантности средних.
Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности.
 2014-02-02
2014-02-02 4671
4671
