Средние величины и изучение вариации

1.Ряды распределения и их основные характеристики.

2.Сущность и значение средних величин. Исходное соотношение средней.

3.Средняя арифметическая и ее свойства.

4.Другие формы средней.

5.Понятие о вариации. Показатели размера и интенсивности вариации.

6. Дисперсия сгруппированных данных. Правило сложения дисперсий. Эмпирическое корреляционное отношение.

j. Построение рядов распределения – важный этап сводной обработки данных наблюдения. От характера представления данных зависят и методы анализа и интерпретация полученных результатов, а в конечном итоге – принятие решений на всех уровнях управления.

Рядом распределения в статистике называют распределение единиц совокупности на группы по какому-либо существенному варьирующему признаку.

Если данные представлены за определенные периоды времени – то они называются рядами динамики, если на какой-то момент времени – то их называют просто рядами распределения.

В зависимости от того, является ли признак, взятый за основу группировки качественным или количественным, различают атрибутивные и вариационныеряды распределения. Ряды распределения, построенные по показателям, не имеющим количественной меры (пол, национальность, профессия и т.д.),называются атрибутивными, а по количественным – вариационными, так как имеет место вариация – количественное различие в величине признака.

Форма построения вариационного ряда зависит от характера изменения изучаемого признака, он может быть в форме дискретного или интервального ряда.

Дискретный ряд - это ряд построенный по дискретным признакам, т.е. с прерывным изменением, которые могут принимать лишь конечное число определенных значений: число детей в семье, численность работающих, тарифный разряд и т.д.

Непрерывный (интервальный) ряд – ряд построенный по признакам с непрерывным значением, т.е. значения их могут отличаться один от другого нам сколь угодно малую величину и в определенных границах могут принимать любые значения, которые задаются как правило в виде интервалов.

Если дискретная вариация проявляется в очень широких пределах, то на ее основе строят интервальные ряды распределения.

Для построения дискретного ряда с небольшим числом вариантов достаточно перечислить все имеющиеся варианты значений признака, а затем подсчитать частоту их повторений.

Существует вид вариационного ряда - ранжированный, который в свою очередь может быть и интервальным и дискретным, его особенность в том, что строится он в порядке возрастания или убывания изучаемого признака.

При построении интервальных рядов распределения необходимо прежде всего установить число групп на которые будет разбита совокупность (см. главу «Группировка статистических данных»), а затем уже строить интервальный вариационный ряд.

Примером интервального вариационного ряда может служить таблица 6.1.

В вариационном ряду распределения различают два основных элемента: варианты и частоты.

Варианты (х) – это отдельные значения группировочного признака, которые он принимает в вариационном ряду.

Числа (f), показывающие как часто встречаются те иные варианты – называются частотами.

Таблица 6.1.

Выполнение норм выработки рабочими цеха

Группы рабочих по выполнению норм выработки, %, х	Число рабочих, f	Частости, w	Накопленная частота, S
в долях	в %
80-90		0,022	2.2
90-100		0,245	24,5
100-110		0,533	53.3
110-120		0,178	17,8
120-130		0,022	2,2
итого		1,000	100,0

Частоты ряда могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных величинах (в долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму:

f₁ f₁

W₁ = ------; W₂ = ------- и т.д.

S f Sf

Аналогичные действия производятся и с долями.

Накопленные частоты (S) показывают сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Если вариационный ряд дан с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала. Полученное отношение называется абсолютная плотность распределения. (р):

p = f / i

Относительная плотность распределения (р¢) – частное от деления частости отдельной группы на размер ее интервала:

р¢ = w / i

Первым этапом изучения вариационного ряда является его графическое изображение. Интервальные ряд изображается столбиковой диаграммой, в которой основания столбиков расположены по оси абсцисс, - это интервалы значений варьирующего признака, а высоты столбиков – частоты, соответствующие масштабу на оси ординат. Диаграмма такого рода часто называется гистограмма (от греческого слова «гистос» - ткань, строение). В случае неравных интервалов гистограмма строится по плотности распределения.

Если имеется дискретный вариационный ряд или используются середины интервалов, то графическое изображение такого ряда называется полигоном (от греч. слова – многоугольник).

По накопленным частотам строится кумулятивная кривая (кумулята) – она особенно удобна для сравнения вариационных рядов. Если поменять местами оси координат в кумуляте – то получится новый вид изображения – огива.

Приведенные в таблице 6.1 данные показывают характерную для многих признаков форму распределения: чаще встречаются значения средних интервалов, реже - крайние (малые и большие). Форма этого распределения близка к рассматриваемому в курсе математической статистики закону нормального распределения. Великий русский математик А.М. Ляпунов доказал, что нормальное распределение образуется, если на варьирующую переменную влияет большее число факторов, ни один из которых не имеет преобладающего значения.

Более детально с анализом форм распределения, и показателями моментов распределения рекомендуется ознакомиться в учебниках по «Общей теории статистики» и «Математическая статистика».

l.Средние величины – самые распространенные формы сводных величин. Главное их значение состоит в их обобщающей функции, т. е. Они дают общую количественную характеристику явления и присущи всем элементам этого явления или процесса.

Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие – средняя должна вычисляться для качественно однородной совокупности. Например, вычислять среднюю цену для качественно разнородных товаров (мясо, молоко, картофель и т.д.) не имеет смысла, но вычислять среднюю цену, например, по мясу (говядина, баранина, конина и т.д.) будет иметь смысл, так как это однородные товары. Для получения однородной совокупности используется и группировка, поэтому расчет средней сочетается с этим методом.

Второе условие – для исчисления средней должны быть использованы массовые данные. Это связано с законом больших чисел, то есть колебания, вызванные случайными отклонениями погашаются и проявляется общее свойство для всей совокупности.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности, но в зависимости от характера числителя она может иметь реальную величину (например, средняя заработная плата, средняя производительность труда) и не иметь непосредственного значения (например, среднее число детей в семье).

При использовании средних в практической работе и научных исследованиях необходимо в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

Приступая к решению конкретной задачи на средние, необходимо определить что является совокупностью, а что признаком и численностью признака. Но такие определения бывают подчас довольно затруднительны, поэтому прежде чем оперировать с цифрами, необходимо составить логическую формулу для вычисления средней, которая называется исходное соотношение средней (ИСС). Формализовать это соотношение можно следующим образом:

Общий объем явления (совокупности)

Средняя величина = ------------------------------------------------

Численность единиц совокупности

Составление ИСС не очень-то простое дело, особенно когда признак является относительной величиной, выражаемой в процентах или коэффициентах. Но именно в этих случаях использование ИСС позволяет абстрагироваться и безошибочно определить необходимую для данного случая форму средней.

Рассмотрим такой пример: мастер и ученик отработали по 8 часов за день, производя, например, номерки для гардероба. На изготовление одного номерка у мастера ушло в среднем – 2 минуты, а у ученика – 6 минут (этот показатель называется трудоемкость изготовления единицы продукции). Требуется определить среднюю трудоемкость изготовления номерка для гардероба, изготовленных мастером и учеником вместе.

С первого взгляда ответ однозначен – 4 минуты (2+6): 2, но, во- первых, данные действия не несут смысловой нагрузки (разве они сделали всего два номерка и потратили всего 8 минут на изготовление номерков?), во-вторых, если сделать проверку и выйти на количество изготовленных деталей, то полученный результат будет совершенно другой. Как поступить? Первоначально выясняем, что такое трудоемкость изготовления 1 детали – это время потраченное в среднем на изготовление изделия. Значит, для ее нахождения необходимо все затраченное время на изготовление всех номерков разделить на их количество. Таким образом ИСС будет иметь вид:

Затраты времени на изготовление деталей

Трудоемкость = ------------------------------------------------------

Количество изготовленных деталей

Затраченное время известно: 8 + 8 (часов), но нам необходимо перевести их в минуты, так трудоемкость в данном случае выражена в минутах. Количество изготовленных деталей находим из определенной нами выше формулы, т.е.:

Затраты времени

Количество = -----------------------------

Трудоемкость

Расчеты будут выглядеть следующим образом:

(8 х 60) + (8 х 60) 480+480 960

--------------------------------------- = ------------ = ---- = 3

((8 х 60): 2) + ((8 х 60): 6) 240 + 80 320

Приведем примеры ИСС, для средней заработной платы:

Общий фонд заработной платы

Средняя зарплата = --------------------------------------

Число работников

Для нахождения среднего процента выполнения плана (%в.п.):

Фактический объем продукции

% в.п.= -------------------------------------------- х 100

плановый объем продукции

и т. д. и т.п.

Области применения средних величин крайне разнообразны: характеристика уровня развития явления, сравнение двух или нескольких уровней, характеристика изменений уровней в динамике, выявление и характеристика связей явлений, расчет нормативов, планирование и прогнозирование. Но главное все же при проведении любых расчетов, и это касается не только средних – это логическая взаимосвязь показателей. Ведь не бывает в реальной жизни тенге², чел² , ведь не суммируем мы килограммы купленного картофеля с его стоимостью. Таким образом, все математические действия в статистике должны нести смысловую нагрузку, так же как и любые деяния в нашей жизни.

l.В математической статистике принято делить средние на две категории: степенные средние и структурные средние. К степенным относятся: арифметическая, геометрическая, гармоническая, квадратическая. Структурные – используются для изучения структуры вариационного ряда. В математической статистике такое деление хотя и имеет место, но в общей теории статистике все же определяющим является социально-экономическое содержание изучаемых явлений и существующими между ними объективными взаимосвязями. Например, ряд чисел 1,2,3. Вычисления с обезличенными цифрами можно производить самые разнообразные, но если за ними стоят, например, конкретные суммы денег у конкретных людей: 1 тыс.тенге, 2 тыс.тенге, 3 тыс.тенге, то будет иметь смысл только применение средней арифметической, если, например, требуется узнать какая в среднем сумма приходится на каждого человека из этой компании. Заметим, что обозначаются средние общепринято ().

= (1+2+3): 3 = 2

Если найдем по средней геометрической:

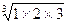= = 1,817

или гармонической:

3 3 18

= -------------- = ------ = ---- = 1, 636

1 + ½ + ⅓ 11/6 11

то они уже не будут иметь смысл.

Арифметическая средняя является наиболее распространенной средней. Она применяется в форме простой средней и взвешенной средней. Простая средняя арифметическая применяется тогда когда значения признака индивидуальны, то есть повторяются только по одному разу (как в примере с суммами денег), или при равенстве частот, тогда формула будет иметь вид:

∑ х

= ------

n

где, х – индивидуальные значения признака (варианты), n – число вариант.

Если значения признака повторяются неоднократно, то есть частоты не равны между собой, то применяется средняя арифметическая взвешенная:

∑ хf

= -----------

∑ f

где f - частота (как часто встречается варианта).

Например, если 1 тыс.тенге имеют 3 человека, 2 тыс.- имеют 10 чел, а 3 тыс. – 4 человека, то в среднем на каждого будет:

∑ хf 1х3 +2х10 + 3х 4 35

= ----------- = ---------------------- = --------- = 2,058

∑ f 17 17

то есть по 2 тысяче 58 тенге на каждого.

Если частоты даны в виде относительных величин, например, долей, сумма которых равна или 1, то формула примет вид:

= ∑ хd

где d – доля частот по каждой группе.

Например, представим вышеизложенные данные (частоты) в виде коэффициентов. Тогда 1 тыс. имеют (3/17) 0,2 части численности, 2 тыс. – 0,6, 3 тыс. – 0,2. Следовательно:

= ∑ хd = 1х0,2 + 2х0,6 + 3х0,2 = 2

Если подсчитать структуру более точно, до сотых, например, то результат будет близок к искомому.

Знание некоторых математических свойств средней арифметической полезно как при ее использовании, так и при ее расчете.

1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю:

∑ (х - )f = 0

2.Если каждое индивидуальное значение признака умножить или разделить на постоянное число (С), то и средняя увеличится или уменьшится во столько же раз:

∑ (х: С)

-----------------= : С

n

Вследствие этого свойства индивидуальные значения признака можно сократить в С раз, произвести расчет средней и результат умножить на С. Так, на практике это свойство находит применение тогда, когда многозначные числа признака выражают в более крупных единицах измерения.

3. Если к каждому индивидуальному значения прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на то же число:

∑ (х + С)

-----------------= + С

n

Это свойство полезно использовать при расчете средней величины из многозначных и слабоварьирующих значений признака, например, роста группы лиц: 179, 183,171,180,169. Для вычисления среднего роста из каждого значения вычитаем 170 и находим среднюю из остатков: (9+13+1+10-1): 5 = 6,4. Средний рост = 6,4 +170 = 176,4

4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится:

∑ х f/c

= ----------- =

∑ f/c

Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерения.

Ряд этих свойств нашел применение в расчете средней способом моментов. Учитывая применяемые в настоящее время компьютерные программы, многократно упрощающие расчеты (например, EXEL) и выполняющие статистический анализ способ моментов на практике не имеет уже должного применения. Ознакомится с ним можно в учебниках «Общая теория статистики».

m. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной ( _кв). Ее формула такова:

_кв =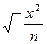

Например, имеются три участка земельной площади со сторонами квадрата: 100, 200, 300 метров. Заменяя разные значения длины сторон на среднюю, мы, очевидно, должны исходить из сохранения общей площади всех участков. Арифметическая средняя величина (100+200+300): 3 = 200 м. не удовлетворяет условию, так как общая площадь трех участков со стороной 200 метров была бы равна: 3 х (200 м)² = 120000 м². В тоже время площадь исходных трех участков равна: 100² + 200² + 300² = 140000 м². правильный ответ дает квадратическая средняя:

_кв = 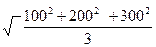= 216 м.

Главной сферой применения в экономико-статистических исследованиях этого вида средних связано с вариациями, о чем будет идти при рассмотрении следующих вопросов.

Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической:

_куб =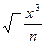

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить среднюю геометрическую. Ее формула такова:

_геом =

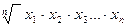
Основное применение геометрическая средняя находит при определении средних темпов роста. Этот вид средней также нашел широкое применение в статистике.

Наибольшее распространение среди других форм средней имеет средняя гармоническая. С ней мы сталкивались при рассмотрении второго вопроса, рассчитывая среднюю трудоемкость изготовления детали. Но находили мы ее используя ИСС. Используя уже известные вам понятия о вариантах и частотах, выясним, что варианты - это трудоемкость каждого изделия, а повторяются они (это частоты) столько раз сколько произведено изделий. Но условие предполагает только наличие произведения варианты и частоты, то есть затрат времени на изготовление продукции. Обозначим это понятие через условное обозначение: xf = w. Также в условие имеются сами варианты (х). Выходит что, частоты не заданы в исходных данных непосредственно, а входят множителем в один из исходных показателей. Следовательно, формула средней гармонической (взвешенной) будет иметь вид:

∑ w

_гарм = -----------

∑ w/x

Средняя гармоническая может быть и невзвешенной. Попробуйте вывести формулу самостоятельно.

К структурным средним относятся Мода (Мо) и медиана (Ме).

Мода – это наиболее часто встречающееся значение признака в совокупности. В дискретном ряду – это будет варианта выраженная целым числом, в интервальном – можно просто указать только интервал.

Медиана – соответствует варианте, стоящей в середине ранжированного вариационного ряда. Положение медианы определяется ее номером:

N_ме = (n +1) /2,

где n – число единиц в совокупности.

n.С изменениями признака мы встречаемся повсеместно: это различие в уровнях оплаты труда, качестве работ, ценах, успеваемости и т.д. и т.п.

Вариация присуща всем без исключения явлениям природы и общества, разве что «число президентов» конкретной структурной единицы не варьирует – все они имеют по одному президенту.

Создатель учения о средних величинах бельгийский статистик А. Кетле по этому поводу писал: «В мире существует общий закон, предназначенный как бы для того, чтобы разливать жизнь во Вселенной; в силу этого закона все живущее подлежит бесконечному разнообразию… Каждый предмет подвержен флюктуациям».

Статистику интересуют только варьирующие признаки, вернее вариация массовых явлений и процессов. Большинство методов статистики – это либо методы измерения вариации, либо методы абстрагирования от нее.

Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц совокупности в один и тот же период или момент времени.

Для характеристики вариации применяется ряд показателей, значение и расчет которых покажем на примере.

Распределение оценок полученных на экзамене по «Общей теории статистики» в двух группах сложилось следующее:

оценка	Количество человек в группе
СТ -1	СТ-2

Определите лучшую группу. Аргументируйте.

Первоначальным действием является определение среднего балла, как обобщающей характеристики совокупности. Но, подсчитав средние балы выясняется, что они совершенно одинаковы.

∑ хf 2х1+ 3х7+ 4х15+5х2 93

₁ = ----------- = ---------------------- = --------- = 3,72

∑ f 25 25

∑ хf 2х9+3х2+4х1+5х13 93

₂= ----------- = ---------------------- = --------- = 3,72

∑ f 25 25

То есть средняя затушевала все различия. После обсуждения (какая все же лучше?) приходим к выводу, что СТ-1 все же лучше: в ней и меньше двоек и больше чем в СТ-2 хороших и отличных оценок, к тому же большинство оценок в ней близки к средней, которая и сама близка к оценке «хорошо». Как доказать эти доводы. Не словами «меньше, больше», «сильнее, слабее» и т.д., а цифрами, фактами, т.е. количественными аргументами. Для этого используются специальные показатели. Рассмотрим их.

1. Размах вариации, Представляет собой разность между максимальным и минимальным значением признака:

R = X max – X min

В данном случаем для обоих групп он будет одинаков:

5-2=3, то есть в данном случае он не работает, а показывает лишь то, что разница между худшей и лучшей оценкой составляет три балла.

2. Среднее линейное отклонение. Показывает, на сколько в среднем отклоняется каждая варианта от ее среднего значения. Поскольку сумма отклонений от средней всегда равна нулю, все отклонения должны быть положительными, поэтому берутся по модулю. Кроме того отклонения должны быть взвешены, так как имеются в наличии частоты. Формула будет иметь вид:

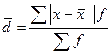
Для невзвешенных данных:

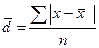
3. Среднее квадратическое отклонение. Модуль считается математической условностью, поэтому, для того чтобы отклонения стали положительными их возводят в квадрат, а затем извлекают квадратный корень. Обозначается этот показатель малой строчной греческой буквой сигма (σ), для взвешенных отклонений формула имеет вид:

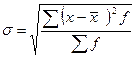
для невзвешенных:

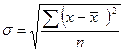
4. Квадрат среднего квадратического отклонения дает величину дисперсии. На дисперсии основаны практически все методы математической статистики. Для взвешенных отклонений она находится по формуле:

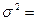
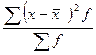
для невзвешенных:

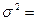
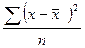
Дисперсию можно определить также по формуле:

- = -

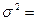
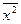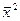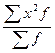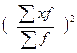
Расчеты по этой формуле применяются тогда, когда варианты выражаются небольшими и не многозначными цифрами.

5. Коэффициент вариации. Это относительная мера варьирования признака. Он имеет очень широкое применение. Применяется для сравнения вариации в разных совокупностях. И что очень важно характеризует однородность совокупности. Если коэффициент вариации не превышает трети, то есть 33%, то совокупность считается однородной, если превышает, то рассчитанная средняя считается ненадежной, нехарактерной и использовать ее в расчетах не рекомендуется.

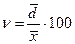
коэффициент вариации рассчитанный по среднему линейному отклонению,

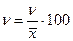
коэффициент вариации рассчитанный по среднему квадратическому отклонению.

Необходимо заметить, что сравнительные расчеты должности вестись по единой методике (или через линейное или через квадратическое отклонения) - в виду свойства мажорантности средних: среднее квадратическое отклонение по своей величине всегда превышает значение среднего линейного отклонения.

Расчет указанных формул в применении к нашей задаче представим в виде вспомогательных таблиц.

СТ-1
x	f	xf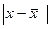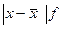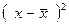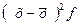
			1,72	1,72	2,96	2,96
			0,72	5,04	0,52	3,64
			0,28	4.2	0,07	1,05
			1,28	2,56	1,64	3,28
				13,52		10,93

СТ-2
x	f	xf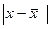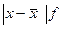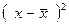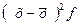
			1,72	15,48	2,96	26,64
			0,72	1,44	0,52	1,04
			0,28	0,28	0,07	0,07
			1,28	16,64	1,64	21,32
				33,84		49,07

Подставив полученные данные в формулы, получим:

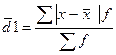= 13,52: 25 = 0,54

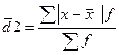= 33,84: 25 = 1,35

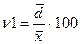= 0,54: 3,72 = 14,5 %

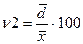= 1,35: 3,72 = 36,3%

Следовательно в группе СТ-2 средняя ненадежна, так как вариация превышает 33%. Следовательно, для группы СТ-1 средняя более типична, и подавляюща часть студентов успевает на 3,72, а значит она лучше.

Опираясь на данные таблиц рассчитайте коэффициенты вариации по среднему квадратическому отклонению.

Кроме исследования вариации количественного признака имеет практическое применение и изучение вариации альтернативного признака, который имеет две взаимоисключающие разновидности. Например, мужчины и женщин, продукция годная и негодная.

Альтернативный признак принимает всего значения: или да или нет. Применив условные обозначения к долям этого соотношения получим:

p +q = 1

где, p – доля единиц обладающая признаком, q – доля единиц не обладающих признаком.

Дисперсия альтернативного признака находится по формуле:

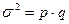
Предельное значение вариации альтернативного признака 0,25. Оно получается при p =q = 0,5

o.Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и, опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих колеблемость индивидуальных значений (вариант) признака. Это можно сделать при помощи метода группировок, когда единицы изучаемой совокупности подразделяются на однородные группы по признаку-фактору. При этом, кроме общей средней для всей совокупности исчисляются средние по отдельным группам. Следовательно, и вариацию сгруппированных данных можно оценить следующими видами дисперсий: Общей дисперсией (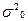), межгрупповой дисперсией ( 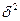-дельта) и средней внутригрупповой дисперсией ().

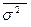Величина общей дисперсии характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц совокупности, и определяется по формуле, уже вам знакомой:

=

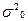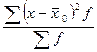
где 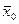- общая средняя арифметическая для всей изучаемой совокупности.

Межгрупповая дисперсия (дисперсия групповых средних) отражает систематическую вариацию произошедшую под влиянием признака, положенного в основу группировки.. проще говоря, измеряет колеблемость групповых средних вокруг общей средней. Находится по формуле:

=

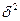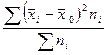
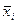-средняя по отдельной группе

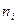- число единиц в определенной группе.

Средняя внутригрупповая дисперсия характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора) положенного в основу группировки. Она определяется по формуле:

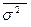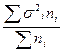= или =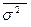

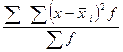
где 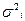-дисперсия по отдельной группе:

=

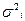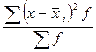
Существует закон связывающей эти три вида дисперсий - величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

= +

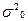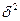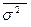
Опираясь на него можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака- фактора положенного в основу группировки. Это покажет коэффициент детерминации:

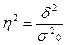
Если извлечь квадратный корень из коэффициента детерминации то получим эмпирическое корреляционное отношение, измеряющее тесноту связи между факторным и результативным признаками:

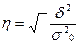
Этот показатель принимает значения от 0 до 1. Чем ближе к 1 тем теснее связь и наоборот. Так, значения до 0,33 – характеризуют слабую связь, от 0,33 до 0,67 – среднюю и от 0,67 до 1 – сильную.

Литература:

Основная:1.2.3,5,7,

Дополнительная: 11.12.14

Задания для СРС:

1. Охарактеризуйте дискретные и интервальные ряды распределения.

2. Как строятся гистограмма и полигон распределения?

3. Каковы особенности нормального распределения?

4. Что представляет собой средняя величина и в чем состоит ее определяющее свойство?

5. Что такое исходное соотношение средней (ИСС)? Аргументируйте первоочередное значение определения ИСС.

6. Назовите условия применения средней арифметической простой и взвешенной? Приведите примеры.

7. Назовите условия применения средней гармонической простой и взвешенной? Приведите примеры.

8. Назовите основные свойства средней арифметической.

9. Для каких целей используется средняя геометрическая?