Математическое ожидание и дисперсия системы случайных величин

Свойства плотности вероятности.

1. Функция .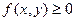

2. .

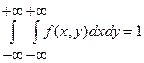3. ,

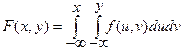где 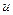и 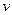- переменные интегрирования.

4.

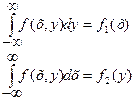
Математическим ожиданием двумерной случайной величины 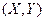называется совокупность двух математических ожиданий М[Х], М[Y], то есть упорядоченных пар М[Х], М[Y], которые определяются равенствами:

а) если Х и Y – дискретные случайные величины:

М[Х]=, : ; .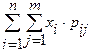

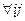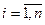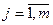М[Y]=.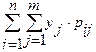

б) если Х и Y – непрерывные случайные величины:

М[Х]=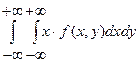

М[Y]= ,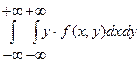

где 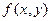- плотность вероятности двумерной случайной величины .

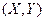Математическое ожиданиеслучайной величины 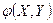, которая является функцией компонент 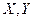двумерной случайной величины 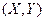, находится аналогично по формулам:

1) М[j(Х, Y)]= 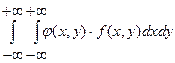- если Х и Y – непрерывные случайные величины;

2) М[j(Х, Y)]=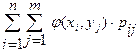, 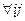: 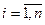; 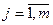- если Х и Y – дискретные случайные величины.