Условное математическое ожидание

Пусть (X,Y) – система дискретных случайных величин. Условным математическим ожиданием дискретной случайной величины Y приусловии, что Х= 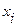, называется величина

М[Y│X= ]=.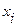

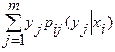Аналогично, условным математическим ожиданием дискретной случайной величины X приусловии, что Y = y_j, называется величина

М[Х│Y= ]=, : ; .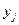

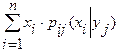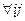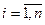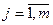Пусть 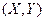- системанепрерывных случайных величин. В этом случае условное математическое ожидание случайной величины Y приусловии, что Х= x_i, определяется равенством:

М[Y│ ]= .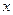

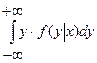Аналогично, условное математическое ожидание случайной величиныX приусловии, что Y = y_j, определяется равенством:

М[Х│ ]=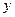

Для характеристики связи между величинами Х и Y служит корреляционный момент:

K_xy = М[ 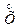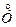]=M[(X – m_x)M(Y – m_y)].

Используя понятие корреляционного момента запишем еще одно свойство дисперсии, а именно - дисперсия суммы двух случайных величин определяется равенством:

D[X+Y] = D[X]+D[Y]+2K_xy

Корреляционный момент иначе называется ковариация и обозначается cov(Х, Y).

Величина корреляционного момента вычисляется по формулам:

а) если Х и Y – дискретные случайные величины:

K_xy=, : ; .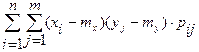

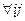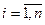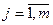б) если Х и Y – непрерывные случайные величины:

K_xy= ,

где 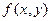- плотность вероятности двумерной случайной величины ,

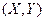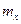, - математические ожидания компонент .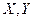

Корреляционный момент удобно вычислять по формуле:

K_xy=М[ХY]-М[Х]М[Y].

Если Х и Y независимы, то K_xy=0. Таким образом, если K_xy 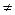0, тослучайные величины Х и Y зависимы. В этом случае случайные величины Х и Y называются коррелированными.

Когда K_xy=0, случайные величины Х и Y называются некоррелированными.

Из рассмотренного свойства корреляционного момента получаем важное следствие. Дисперсия суммы двух случайных величин равна сумме их дисперсий если величины X и Y независимы, т.е.

D[X+Y] = D[X]+D[Y]+2K_xy

Коэффициент корреляции (r_xy) для двух случайных величин Х и Y есть безразмерная величина:

r_xy=,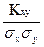

где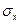,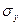- средние квадратические отклонения величин Х и Y соответственно.

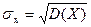
Коэффициент корреляции характеризует степень линейной зависимости двух случайных величин Х и Y.