Определение. Случайный вектор 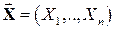 называется дискретным, если множество его возможных значений
называется дискретным, если множество его возможных значений 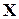 конечно или счетно:
конечно или счетно:
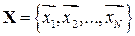 или
или 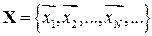 ,
,
где 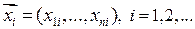 .
.
Из определения следует, что случайный вектор является дискретным тогда и только тогда, когда все его координаты 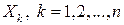 , являются дискретными случайными величинами.
, являются дискретными случайными величинами.
Рассмотрим более подробно случай двумерного дискретного случайного вектора  , принимающего конечное число значений (случай счетного числа значений рассмотреть самостоятельно). Для полной вероятностной характеристики такого дискретного случайного вектора
, принимающего конечное число значений (случай счетного числа значений рассмотреть самостоятельно). Для полной вероятностной характеристики такого дискретного случайного вектора  достаточно указать все его возможные значения
достаточно указать все его возможные значения 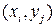 и вероятности
и вероятности 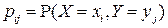 , с которыми эти значения принимаются,
, с которыми эти значения принимаются, 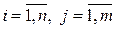 (предполагается, что случайная величина
(предполагается, что случайная величина  принимает
принимает 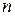 значений, а случайная величина
значений, а случайная величина  принимает
принимает 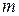 значений, так что у вектора
значений, так что у вектора  возможных значений
возможных значений 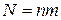 ).
).
Как и в одномерном случае, подобную информацию о дискретном случайном векторе  записывают в виде таблицы, но с двумя входами:
записывают в виде таблицы, но с двумя входами:
  | 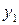 | 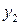 | … | 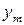 | (3.2) |
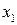 | 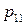 | 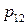 | … | 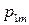 | |
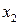 | 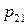 | 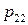 | … | 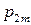 | |
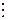 | 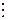 | 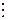 | 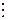 | 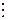 | |
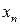 | 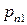 | 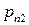 | … | 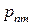 |
которую называют законом распределения дискретного случайного вектора  (двумерным дискретным законом распределения или совместным законом распределения дискретных случайных величин
(двумерным дискретным законом распределения или совместным законом распределения дискретных случайных величин  и
и  ).
).
При этом, поскольку события 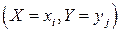 ,
, 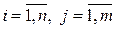 , образуют полную группу событий, то вероятности
, образуют полную группу событий, то вероятности 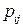 удовлетворяют условию нормировки:
удовлетворяют условию нормировки:

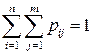 .
.
По двумерному закону распределения вероятность попадания дискретного случайного вектора  в любое борелевское множество
в любое борелевское множество 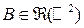 определяется по формуле:
определяется по формуле:
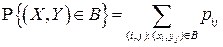 .
.
В частности, при 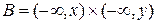 получается следующее выражение для функции распределения
получается следующее выражение для функции распределения 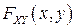 дискретного случайного вектора
дискретного случайного вектора  :
:
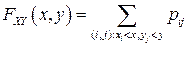 .
.
(сравнить с одномерным случаем, когда 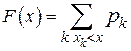 ).
).
График функции распределения 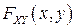 дискретного случайного вектора
дискретного случайного вектора  является кусочно-постоянным со скачками в точках
является кусочно-постоянным со скачками в точках 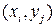 , являющихся его возможными значениями, величина которых определяется вероятностями
, являющихся его возможными значениями, величина которых определяется вероятностями 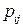
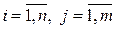 .
.
Одномерные законы распределения каждой из случайных величин  и
и  в отдельности (маргинальные законы распределения) дискретного случайного вектора
в отдельности (маргинальные законы распределения) дискретного случайного вектора  являются дискретными и находятся по двумерному закону распределения следующим образом:
являются дискретными и находятся по двумерному закону распределения следующим образом:
Так как событие 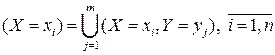 , то в силу аддитивности вероятности
, то в силу аддитивности вероятности
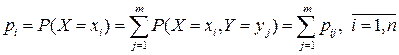 . (3.3)
. (3.3)
Таким образом, закон распределения случайной величины  имеет вид:
имеет вид:
 | 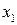 | 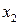 | 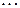 | 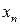 |
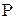 | 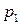 | 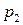 | 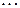 | 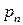 |
где в соответствии с (3.3) вероятность 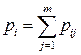 получается суммированием в
получается суммированием в 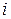 -ой строке таблицы (3.2) вероятностей
-ой строке таблицы (3.2) вероятностей 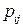 ,
, 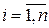 .
.
Аналогично, вероятности
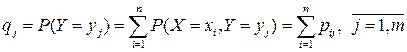 (3.4)
(3.4)
и поэтому закон распределения случайной величины  имеет вид:
имеет вид:
 | 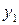 | 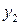 | 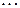 | 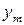 |
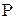 | 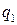 | 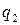 | 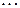 | 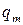 |
где в соответствии с (3.4) вероятность 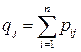 получается суммированием в
получается суммированием в 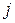 -ом столбце таблицы (3.2) вероятностей
-ом столбце таблицы (3.2) вероятностей 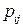 ,
, 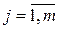 .
.
Многомерный случай дискретного случайного вектора 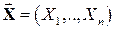 полностью аналогичен двумерному, только менее нагляден и имеет громоздкую индексацию. Так, закон распределения n -мерного дискретного случайного вектора
полностью аналогичен двумерному, только менее нагляден и имеет громоздкую индексацию. Так, закон распределения n -мерного дискретного случайного вектора 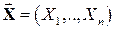 определяется набором вероятностей
определяется набором вероятностей 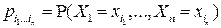 , где
, где 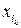 - значения координаты
- значения координаты 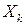 ,
, 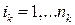 ,
, 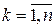 .
.
 2015-06-28
2015-06-28 6986
6986
