Прогнозирование качества из основе спектрального представления процессов, происходящих в конструкциях

Электронная аппаратура и ее отдельные устройства подда­ются прогнозированию качества на основе анализа некоторых характеристик случайного процесса. Эффективными являются те характеристики, которые отражают определенный физи­ческий образ или причину возникновения отказов. В этом смысле наиболее удобна спектральная плотность или энергети­ческий спектр случайного процесса.

Спектральная плотность характеризует распределение мощ­ности случайного процесса по частотному диапазону. При ис­следовании детерминированных сигналов, особенно регулярных импульсных, широкое применение имеет гармонический анализ, позволяющий представить исследуемый сигнал в виде суммы спектральных гармонических составляющих. Применить непо­средственно гармонический анализ к случайному процессу, опи­сываемому, например функциями распределения, невозможно, однако, если известна корреляционная функция процесса, то рассматривая ее как неслучайную, можно определить энерге­тический спектр.

Корреляционная функция является четной, поэтому ее раз­ложение на некотором интервале — Т ÷ + Т состоит из четных гармоник, оно называется спектром дисперсий:

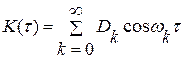(2.1)

где коэффициент D_k определяется по формуле

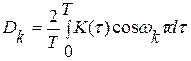(2.2)

Спектр дисперсии, при разло­жении корреляционной функции на конечном интервале, является линейчатым (рис. 2.11).

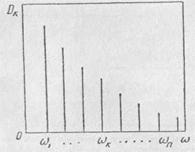
Рис. 2.11. Линейчатый спектр дис­персии

Введем обозначение средней плотности дисперсии или спектральной плотности S(ω_k) = D_k/Δω.

Следовательно, D_{k =} S(ω_k)*Δω.

Подставив значение D_k в формулу (2.1), получим

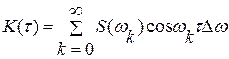
При Т→∞ дискретный аргумент ω_к переходит в непрерывный аргумент ω, а сумма — в интеграл, называемый интегралом Фурье, тогда

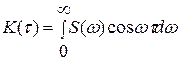(2.3)

Подставив значение D_k в формулу (2.2), получим

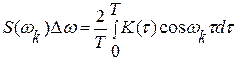
Учитывая, что Δω=2π/Т, находим

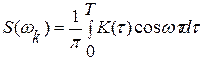
Устремив Т→∞ дискретный аргумент ω_к переходит в непрерывный аргумент ω. В окончательном виде спектральная плотность получает значение

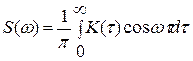(2.4)

Формулы (2.3), (2.4) представляют собой прямое и обратное преобразование Фурье. Они позволяют делать переход из вре­менной области в частотную, и наоборот.

Интересным является случай, когда τ = 0. При этом

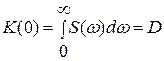
Таким образом, интеграл от спектральной плотности равен дисперсии. Этот результат исключительно важен. Он показы­вает, что площадь под кривой спектральной плотности равна средней мощности процесса, т. е. дисперсии.

В свою очередь, при ω=0

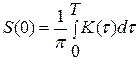
Следовательно, с точностью до множителя S(0) пропорцио­нальна площади под кривой корреляционной функции.

Возвращаясь к вопросу прогнозирования, можно отметить, что спектральная плотность, являясь носителем информации о частотном составе случайного процесса в конструкции, может служить информативной характеристикой показателей качества.

Пример — прогнозирование форм дискретных сигналов в цепях ЭВМ, прогнозирование шумовых характеристик усили­тельных устройств, прогнозирование работоспособности элект­ромеханических устройств систем охлаждения и т. д.

Дисперсия характеризует мощность исследуемого процесса, например, вибропроцесса, происходящего в конструкции. Если процесс стационарен, что соответствует нормальному функци­онированию объекта то dD/dt=0.

Если происходят изменения в конструкции, то они вызывают изменения вибропроцесса, а следовательно, дисперсия вибропро­цесса изменяется. При известном исходном значении дисперсии D_исх и допустимом ее значении D_д можно определить прогнози­руемое время t_п работы объекта с учетом скорости изменения дисперсии

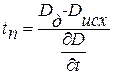
Описанный метод прогнозирования мало эффективен и ана­логичен прогнозированию, рассмотренному ранее. Метод не дает ответа, в чем причины отказа, так как дисперсия не содержит информации о частотном содержании процесса. В связи с этим прогнозирование, основанное на анализе спектральных харак­теристик, является предпочтительным. В данном случае опреде­ленным участкам спектра или отдельным спектральным состав­ляющим можно поставить в соответствие физический образ или причину возникновения рассматриваемых спектральных состав­ляющих.

Предположим, что в конструкцию аппаратуры входит систе­ма принудительного охлаждения, в составе которой имеется электродвигатель. Спектр его собственных вибраций, обуслов­ленный наличием вынужденных сил, известен. При установив­шемся движении ротора он является линейчатым. Первая гар­моника проявляется на частоте вращения ротора ω_р, она связана с его статической и динамической разбалансированностью, вторая спектральная составляющая ω₂ возникает за счет оваль­ности оси ротора и овальности внутреннего кольца подшип­ника. Аналогично можно установить и для других составля­ющих спектра вибрации двигателя физическую причину их возникновения. Следовательно, в данном случае при оценке состояния объекта оценивается качество отдельных элементов конструкции.

Таким образом, если известен линейчатый спектр вибриру­ющего объекта, имеющий вид

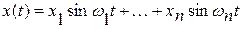
то, приписав физический признак каждой спектральной состав­ляющей, можно организовать «инструментальное» наблюдение за процессом, а следовательно, и за скоростью изменения отдельных спектральных составляющих. Это позволяет определить прогно­зируемое время работоспособности по отдельным параметрам

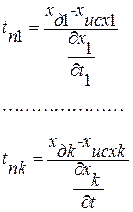
где x_дi, x_исхi — допустимое и исходное значение амплитуд вибра­ции соответственно.

Наименьшее из всех t_пi является прогнозируемым временем работоспособности всего исследуемого объекта.

Аналогичные рассуждения могут быть отнесены и к непре­рывному спектру. В этом случае физической причине возникно­вения вибрации приписываются отдельные участки спектра.

Описанную методику можно распространить на прогнозиро­вание работоспособности различных объектов, включая ЭВМ. Необходимо лишь отслеживать спектры сигналов в основных сигнальных цепях при организации прогнозирования.