Решение задач методом ГМТ заключается в следующем:
А) задача формулируется так, чтобы ее решение сводилось к нахождению фигуры, удовлетворяющей одному или нескольким условиям.
Б) Если условие одно, то решением задачи будет соответствующее ГМТ. Если же условий несколько, то, отбросив одно из них, мы получим новую задачу, решением которой будет одно или несколько ГМТ. Это ГМТ обыкновенно является известным и легко строится.
В) После этого, приняв во внимание отброшенное условие и отбросив какое-либо другое условие, получим новое ГМТ.
Г) Точки, являющиеся решением задачи (т.е. удовлетворяющие всем ее условиям), должны принадлежать как первому, так и второму ГМТ. Значит, они должны принадлежать их пересечению.
Задача будет иметь решение или нет в зависимости от того, будут или нет ГМТ иметь общие точки. Она будет иметь столько решений, сколько имеется точек пересечения.
Приведем примеры.
ПРИМЕР 4. Построить окружность, касающуюся данной окружности в данной точке В и данной прямой МN. (рис. 5).
Анализ. Предположим задача решена, т.е. окружность с центром в точке О1 удовлетворяет условиям задачи, т.е. касается окружности с центром О в точке В и касается прямой МN. Тогда центры искомых окружностей лежат на прямой ОВ (ГМТ № 6). Проведя через В касательную к обеим окружностям до пересечения с МN в точке К, получаем, что искомая окружность вписана в угол NКВ. Значит, ее
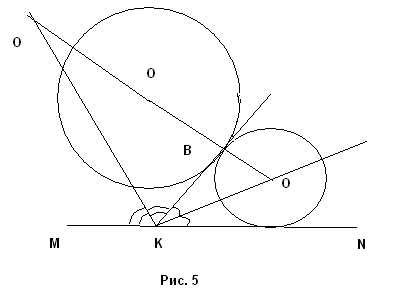
центр лежит на биссектрисе этого угла (ГМТ № 11); проведя биссектрису смежного угла, получим второе решение.
Построение. Через точки В и О проводим прямую. Затем через В проводим касательную к заданной окружности. Получаем углы МКВ и ВКN. Строим биссектрисы этих углов. Их пересечения с прямой ОВ дадут центры искомых окружностей - О1 и О2. Строим окружности с центром в точке О1 радиуса О1В и окружность с центром в точке О2 радиуса О2В.
Доказательство следует из построения.
Исследование. Число решений зависит от взаимного расположения окружности О и прямой МN. Возможны 3 случая.
1) Прямая МN не имеет с окружностью общих точек. В этом случае задача имеет, как мы уже разобрали, два решения. (Разберите самостоятельно случай, когда MN ║ ВО).
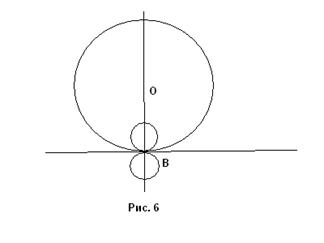
2) Прямая MN касается окружности. Если касание происходит в точке В, то задача имеет бесконечно много решений (рис. 6). Все центры искомых окружностей находятся на прямой ОВ.
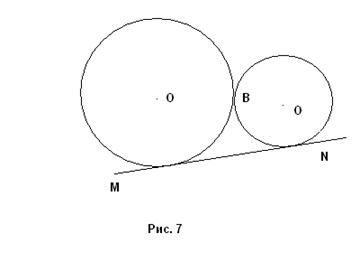
Если точка В не совпадает с точкой касания. Тогда задача имеет одно решение (рис. 7).
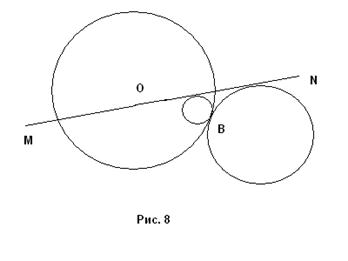
3) Прямая MN пересекает данную окружность. Если одна из точек пересечения совпадает с точкой В, то решений нет. Если же MN не проходит через точку В, то решений 2 (рис. 8).
ПРИМЕР 5. Построить треугольник по основанию а, высоте ha и боковой стороне b.
Анализ. Предположим, что треугольник АВС построен и у него ВС = a, СА = b и высота, опущенная из вершины А, равна ha. Тогда множество всех вершин треугольников с данным
основанием a и высотой ha будут лежать на двух прямых, параллельных ВС и отстоящих от нее на расстоянии ha (ГМТ № 10).
Далее, т.к. СА = b, то точка А находится на данном расстоянии от точки С, а, значит, лежит на окружности радиуса b с центром в точке С (ГМТ № 1). Значит, точка А является пересечением двух ГМТ и, следовательно, определяется.
Построение. На произвольной прямой MN от произвольной точки В откладываем отрезок ВС = a. Из любой точки К прямой MN проводим прямую FK ^ MN и на FK от K в обе стороны откладываем отрезки KT и KE равные ha . Через Т и Е проводим прямые n и m, перпендикулярные ТЕ. Из точки С проводим окружность радиуса b.
Точка пересечения этой окружности с прямыми m и n является искомой точкой А. Соединяем ее с точками В и С. Треугольник АВС - искомый.
Доказательство. В треугольнике АВС основание ВС = a по построению, вершина А удалена от основания на расстояние ha , а боковая сторона АС = b.
Исследование. Если b > ha, то имеем четыре решения. Т.к. окружность радиуса a пересечет прямые m и n в четырех точках.
Если b = ha , то получаем два решения, т.к. прямые m и n будут касаться окружности.
Если b < ha , то решений нет. (Сделайте рисунки самостоятельно!)
 2014-02-02
2014-02-02 9674
9674
