Подобие при решении задач на построение

Во многих случаях бывает удобно строить не искомую фигуру, а начать с построения фигуры, ей подобной, после чего нетрудно перейти к требуемой. В этом случае данные для построения фигуры разделяются на два класса: одни дают возможность построить фигуру, подобную искомой, а другие служат для того, чтобы от этой фигуры перейти к требуемой. Этот прием особенно удобен в тех случаях, когда только одна из данных величин определяет какой-нибудь линейный элемент искомой фигуры, а все другие представляют собой углы или отношения сторон. Например, если для построения треугольника даны два угла или угол и отношение сторон, заключающих этот угол, или отношение трех сторон и, кроме того, один линейный элемент: сторона, высота, медиана, биссектриса, радиус вписанной или описанной окружности и т.д., то вначале, не обращая внимания на данный линейный элемент, строят фигуру, подобную искомой, а потом, вводя требуемую линию, переходят к искомой фигуре. Метод подобия успешно применяется при решении задач на вписывание одних фигур в другие.

Рассмотрим примеры.

ПРИМЕР 12. Построить треугольник по двум углам и медиане, проведенной из вершины третьего угла.

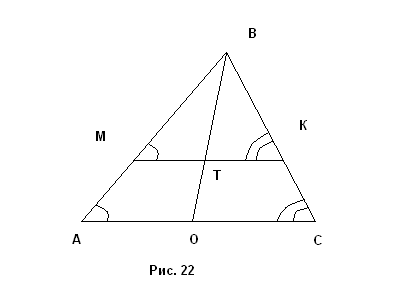
Анализ. Пусть треугольник АВС искомый (рис.22). Треугольники подобны, если два угла одного треугольника равны двум углам другого треугольника, в подобных треугольниках сходственные медианы пропорциональны. Построим произвольный треугольник МВК, два угла которого равны данным; он будет подобен искомому. В этом треугольнике проведем медиану из вершины третьего угла. Пусть ВТ – медиана. Тогда коэффициент подобия – отношение данной медианы к получившейся при построении треугольника МВК, подобного искомому.

Построение. Построим произвольный треугольник МВК, два угла которого равны данным; он будет подобен искомому. В этом треугольнике проведем медиану из вершины третьего угла. Пусть ВТ – медиана. На ВТ от точки В отложим отрезок, равный длине данной медианы – получим точку О. Через О проведем прямую параллельную l прямой МК. Пусть А – точка пересечения продолжения ВМ за точку М с прямой l, а С – точка пересечения продолжения ВК за точку К с прямой l. Треугольник АВС искомый.

Доказательство. Из построения следует, что треугольник МВК подобен треугольнику АВС. Значит, два угла А и В последнего равны заданным. Кроме того, медиана ВО имеет заданную длину, т.е. треугольник обладает всем заданным условиям.

Исследование. Задача всегда имеет решение и притом одно, если сумма заданных углов меньше 180^о.

ПРИМЕР 13. В данный треугольник вписать квадрат так, чтобы две его вершины лежали на основании треугольника, а две другие – на сторонах треугольника.

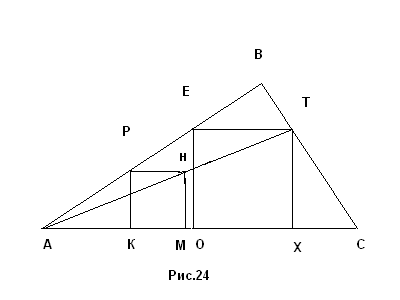
Решение. Пусть АВС – данный треугольник (рис.24). Построим произвольный квадрат МКРН так, чтобы М и К лежали на АС, а Р лежала на АВ. Проведем луч АН. Пусть Т – точка пересечения этого луча со стороной ВС. Проведем отрезки ТЕ ║АС, ТХ ║РК, ЕО║ТХ. Четырехугольник ОЕТХ – искомый.

Доказательство. DАНМ¥DАТХ, значит ТХ^АС и 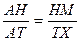. DАРН¥DАЕТ, значит ЕТ║РН и 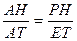. Отсюда ЕТ=ТХ и ÐЕТХ=90^о. Аналогично показывается, что ЕТ=ЕО, т.е. ОЕТХ – квадрат.