8.1. Построение уклона и конусности
Уклон – это величина, которая характеризует наклон одной линии по отношению к другой. Уклон i прямой АС относительно прямой АВ (рис. 23) определяется как отношение разности высот двух точек А и С к горизонтальному расстоянию между ними.
 . (1)
. (1)
Уклон может быть выражен простой дробью, десятичной или в процентах.
 Рис. 23. Уклон прямой Рис. 23. Уклон прямой |  Рис. 24. Построение прямой с уклоном 1:5 Рис. 24. Построение прямой с уклоном 1:5 |
Задача. Через точку А провести прямую АС с уклоном 1:5 к горизонтальной прямой (рис. 24). Из точки А проводят горизонтальный луч и откладывают на нем пять произвольных равных отрезков. На перпендикуляре, восстановленном из конечной точки В, откладывают одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1:5.
Конусность К определяется как отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию между ними (рис. 24).
 (2)
(2)
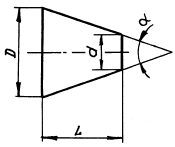 Рис. 24. Конусность Рис. 24. Конусность |  Рис. 25. Построение конусности 1:5 Рис. 25. Построение конусности 1:5 |
Конусность, как и уклон, выражается простой дробью, десятичной или в процентах. На рис. 25 показано построение конусности 1:5. ВС=FЕ.
8.2 Сопряжения
Касание есть плавный переход одной линии в другую. Сопряжение есть плавный переход одной линии в другую, выполненный при помощи промежуточной линии. Чаще всего промежуточной линией служит дуга окружности.
Построение сопряжений основано на следующих геометрических положениях:
а) переход окружности на прямую только тогда будет плавным, когда данная прямая является касательной к окружности (рис. 25, а). Радиус окружности, проведенный в точку касания А, перпендикулярен к касательной прямой;
б) переход в данной точке А с одной окружности на другую только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 26, б).

Рис. 25. Основные понятия сопряжения.
Точка касания А и центры окружностей О1 и О2 лежат на одной прямой. Касание называется внешним, если центры О1 и О2 располагаются по разные стороны от касательной  (рис. 26,б), и внутренним, если центр находится по одну сторону от общей касательной (рис. 26, в).
(рис. 26,б), и внутренним, если центр находится по одну сторону от общей касательной (рис. 26, в).
В теории сопряжений применяются специфические термины, а именно (рис. 26, г): точка О – центр сопряжения; R – радиус сопряжения: точки А и В – точки сопряжения; дуга АВ – дуга сопряжения.
Решение задач на построение сопряжений основано на методе геометрических мест.
Геометрическим местом (ГМ) центров окружности сопряжения касательной к прямой  является прямая, параллельная данной и отстоящей от нее на расстоянии радиуса окружности сопряжения (рис. 27, а).
является прямая, параллельная данной и отстоящей от нее на расстоянии радиуса окружности сопряжения (рис. 27, а).
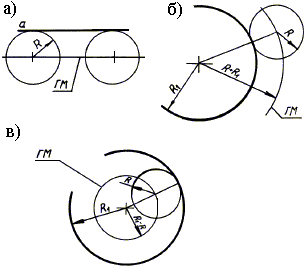
Рис. 27. Геометрические места
Геометрическим местом центров окружности сопряжения, касательной к сопрягаемой окружности, является окружность, радиус которой равен сумме радиусов окружности сопряжения и окружности сопрягаемой для внешнего сопряжения (рис. 26, б) и разности радиусов этих окружностей (рис. 26, в) для внутреннего сопряжения.
Алгоритм решения задач на построение сопряжений двух линий при заданном радиусе сопряжения может быть сформулирован следующим образом:
· Построить геометрическое место центров окружности сопряжения для одной из сопрягаемых линий.
· Построить аналогичное геометрическое место центров для второй сопрягаемой линии.
· Точка пересечения построенных геометрических мест является центром сопряжения.
· Определить точку сопряжения на первой из сопрягаемых линий.
· Определить точку сопряжения на второй из сопрягаемых линий.
· В границах между точками сопряжений провести дугу сопряжения.
Построение сопряжения двух прямых l1 и l2 дугой радиуса R (рис.28, а, б) в соответствии с приведенным выше алгоритмом, осуществляется следующим образом:
– на расстоянии, равном R, проводим ГМ1,параллельно прямой l1;

Рис. 28. Построение сопряжение двух пересекающихся прямых
– на таком же расстоянии, параллельно l2 , проводим ГМ2 (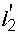 )
)
– в пересечении  и
и 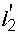 отмечаем точку О – центр сопряжения;
отмечаем точку О – центр сопряжения;
– опускаем из О перпендикуляры на l1 и l2. Соответственно получаем точки А и В – точки сопряжения;
– с центром в точке О радиусом R между точками А и В проводим дугу сопряжения.
Сопряжение прямой с окружностью
В общем случае построение сопряжения окружности m радиуса R1 и прямой l окружностью радиуса R (рис. 28, а, б) производится следующим образом:
– на расстоянии R параллельно l проводим  (ГМ к прямой);
(ГМ к прямой);
– с центром в точке О1 проводим  (ГМ к окружности), радиусом равным сумме R и R1 (рис.29, а – внешнее сопряжение) или радиусом равным разности R и R1 (рис.28, б – внутреннее сопряжение);
(ГМ к окружности), радиусом равным сумме R и R1 (рис.29, а – внешнее сопряжение) или радиусом равным разности R и R1 (рис.28, б – внутреннее сопряжение);
– точка О пересечения  и
и  является центром сопряжения;
является центром сопряжения;
– опускаем из О перпендикуляр на прямую l. Получаем точку сопряжения А;
– через О и О1 проводим прямую и отмечаем точку сопряжения В пересечения ее с окружностью m;
– с центром в точке О радиусом R между точками А и В проводим дугу сопряжения.

Рис. 29. Построение сопряжения прямой линии с окружностью
Сопряжение двух окружностей
При построении внешнего сопряжения двух окружностей m1 и m2 дугой заданного радиуса R (рис.30) центр сопрягающей дуги – точка О – определяется пересечением двух геометрических мест  и
и  – вспомогательных окружностей радиусов R+R1 и R+R2, проведенных соответственно из центров сопрягаемых окружностей, т.е. из точек О1 и О2. Точки сопряжения А и В определяются как точки пересечения заданных окружностей с прямыми ОО1 и ОО2.
– вспомогательных окружностей радиусов R+R1 и R+R2, проведенных соответственно из центров сопрягаемых окружностей, т.е. из точек О1 и О2. Точки сопряжения А и В определяются как точки пересечения заданных окружностей с прямыми ОО1 и ОО2.
Внутреннее сопряжение дуг радиусов R1 и R2 дугой радиуса R показано на рис. 31.

Рис. 31. Внешнее сопряжение двух окружностей

Рис. 31. Внутреннее сопряжение двух окружностей
Для определения центра О дуги сопряжения проводим из точек О1 и О2 вспомогательные дуги  и
и  – два геометрических места – радиусами R–R1 и R–R2. Точка пересечения этих дуг является центром сопряжения. Из точки О через точки О1 и О2 проводим прямые до пересечения с окружностями m1 и m2 и получаем точки сопряжения А и В. Между этими точками и проводится дуга окружности сопряжения радиуса R с центром в точке О.
– два геометрических места – радиусами R–R1 и R–R2. Точка пересечения этих дуг является центром сопряжения. Из точки О через точки О1 и О2 проводим прямые до пересечения с окружностями m1 и m2 и получаем точки сопряжения А и В. Между этими точками и проводится дуга окружности сопряжения радиуса R с центром в точке О.
При смешанном сопряжении (рис. 32) центр сопряжения О определяется в пересечении двух геометрических мест – вспомогательных окружностей радиусов R+R1 и R–R2, проведенных соответственно из центров О1 и О2. Точки сопряжения А и В лежат на пересечении линий центров ОО1 и ОО2 с дугами заданных окружностей.

Рис. 32. Построение смешанного сопряжения двух окружностей
Построение касательных прямых
Построение касательных к окружностям основано на том, что касательная прямая перпендикулярна к радиусу окружности, проведенному в точку касания.
Построение касательной к окружности из точки А, лежащей вне окружности (рис. 33). Отрезок ОА, соединяющий данную точку А с центром О окружности, делим пополам и из полученной точки О1, как из центра, описываем вспомогательную окружность радиусом О1А. Вспомогательная окружность пересекает заданную в точке В, являющейся точкой касания. Прямая АВ будет касательной к окружности, т.к. угол АВО прямой, как вписанный во вспомогательную окружность и опирающийся на ее диаметр.
Построение касательной к двум окружностям. Касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон от касательной.

Рис. 33. Построение касательной к окружности
Для построения внешней касательной к окружностям радиусов R1 и R2 (рис. 34) поступаем следующим образом:
– из центра О2 большей окружности проводим вспомогательную окружность радиусом R2–R1;
– отрезок О1О2 делим пополам;
– с центром О3 проводим вспомогательную окружность радиусом О3О2;
– отмечаем точки пересечения двух вспомогательных окружностей - М и N;
– через точку О2 и полученные точки проводим прямые до пересечения с окружностью радиуса R2. Получаем точки В и D;
– из центра О1 проводим прямые О1А и О1С соответственно параллельные О2В и О2D до пересечения с окружностью радиуса R1 в точках А и С.
Прямые АВ и СD – искомые внешние касательные к двум окружностям.

Рис. 34. Построение внешней касательной к двум окружностям
Построение внутренней касательной к двум окружностям радиусов R1 и R2 (рис. 35).

Рис. 35. Построение внутренней касательной к двум окружностям
Из центра одной из окружностей, например из О1, проводим вспомогательную окружность радиусом R1 + R2. Делим отрезок О1О2 пополам и из полученной точки О3 проводим вторую вспомогательную окружность радиусом О1О3. Точки М и N пересечения вспомогательных окружностей соединяем прямыми с центром О1 и на их пересечении с окружностью радиуса R1 получаем точки касания А и C. Из точки О2 проводим прямую, параллельную О1А и получаем точку касания В на окружности R2. Аналогично строится точка D. Прямые АВ и СD – искомые внутренние касательные к двум окружностям.
8.2 Лекальные кривые
Очертания многих элементов деталей в машиностроении, в строительных конструкциях и различных инженерных сооружениях имеют кривые линии.
Кривые, графическое построение которых производят циркулем, называются циркульными кривыми (окружности, коробовые кривые, завитки).
Кривые, графическое построение которых выполняется с помощью лекал, называются лекальными кривыми (эллипс, парабола, гипербола и т.д.).
Построение эллипса
Эллипсом называется геометрическое место точек М плоскости, сумма расстояний которых от двух данных точек F1 и F2 есть величина постоянная и равна отрезку АВ (рис. 36,а).
Точки F1 и F2 называются фокусами эллипса; отрезок АВ - большой осью; отрезок СD, перпендикулярный к АВ – малой осью; точка О – центром эллипса. Каждой точке эллипса соответствуют две точки, расположенные симметрично относительно большой и малой осей, и одна точка, расположенная симметрично относительно центра эллипса О. На рис. 36,б, а точки, симметричные М, обозначены М1, М2 и М3.
Прямая, проходящая через центр эллипса, называется его диаметром. Большая и малая оси называются главными диаметрами эллипса. Два диаметра эллипса называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру

Рис. 36. Эллипс
Рассмотрим один из способов построения эллипса по большой АВ и малой СD осям (рис. 37, а,б).
Из центра О проводим вспомогательные окружности диаметрами соответственно равным величине большой оси эллипса АВ и малой СD. Для построения любой точки J эллипса (рис. 37,а) из центра О проводим любую секущую прямую и отмечаем точки i и i1 пересечения ее со вспомогательными окружностями. Из точки i на большой окружности проводим прямую, перпендикулярную большой оси АВ, через точку i1 – прямую, перпендикулярную малой оси СD. Точка J пересечения этих прямых является искомой точкой эллипса. Помня о свойстве симметрии эллипса, определяем J1, J2 и J3.
В практической работе (рис.37,б) секущие прямые проводят через точки деления большой окружности на 12 и более равных частей.

Рис. 37. Построение эллипса по большой АВ и малой СD осям
 2015-10-22
2015-10-22 2809
2809
