2014-02-02
567
Чтобы его строки (либо столбцы) были линейно зависимы.
Пусть дана система, содержащая m линейных уравнений с n неизвестными:
5.1.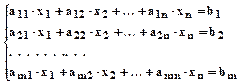 
Введем следующие обозначения.
5.2.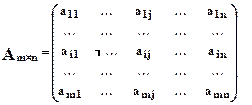 
, 
- матрица системы - ее расширенная матрица.
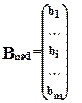- столбец свободных членов. 
- столбец неизвестных.
Если столбец свободных членов нулевой, то систему называют однородной.
Расширенная матрица 5.2. полностью задает систему 5.1.
Систему 5.1. можно задать также в виде матричного уравнения:
5.3.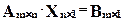 
.
5.3.1. Система 5.1. и матричное уравнение 5.3. эквивалентны.
5.3.2. Теорема Кронекера-Капелли
Для того чтобы система 5.1. была разрешима, необходимо и достаточно, чтобы ранг расширенной
матрицы был равен рангу матрицы системы.
5.3.3. Если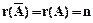 
, то система имеет единственное решение.
5.3.4. Если 
, то система не имеет решений.
5.3.5. Однородная система всегда разрешима, причем линейная комбинация векторов, являющихся решениями
