Виды нелинейных регрессии и определение их параметров с помощью линеаризации

ТЕМА №3. НЕЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

Соотношение между социально-экономическими явлениями далеко не всегда можно выразить линейными функциями. В этом случае прибегают к использованию нелинейных регрессий.

Различают два основных класса нелинейных моделей или регрессий:

1) регрессии, нелинейные относительно факторной переменной х, но линейные относительно параметров уравнения а, b, c и т.д., т.е. зависимая переменная у линейно связана с этими параметрами, например

- полиномиальные функции различных порядков, например, парабола (полином второго порядка) 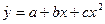; кубическая функция (полином третьего порядка) 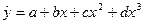и т.д.;

- гипербола ;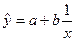

2) регрессии, нелинейные по параметрам модели а, b, c и т.д., например

- степенная функция ;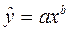

- показательная функция ;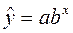

- экспоненциальная функция ;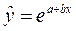

- обратная функция 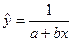и другие.

Рассмотрим подробнее первый класс нелинейных моделей. Общий вид полиномиальной функции n -го порядка или n -степени можно представить в виде следующей формулы:

.

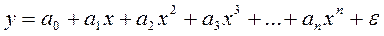Полиномиальные функции характеризуют процессы с монотонным развитием и отсутствием пределов роста. Поставленному условию отвечает большинство экономических показателей. Наиболее часто из полиномиальных функций используется полином второго порядка или парабола:

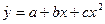или .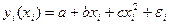

Эта функция характеризует равноускоренное развитие процесса (равноускоренный рост или снижение уровней).

Достаточно часто для описания экономических процессов (например, для изучения зависимости затрат на единицу продукции от объемов производства) применяют гиперболу, которая также как и полиномиальные функции относится к первому классу нелинейных моделей:

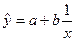или .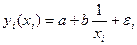

Определение параметров уравнений параболической регрессии осуществляется с помощью метода наименьших квадратов, в результате применения которого получаются системы уравнений, решая которые, находят параметры уравнения регрессии a, b, c:

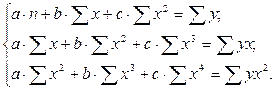
Данная система уравнений может быть решена различными методами. Рассмотрим метод Крамера – метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы.

Матрица системы имеет вид:

.

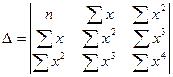Частные матрицы получаются путем заметы i -го столбца матрицы системы столбцом свободных членов:

; ; .

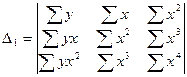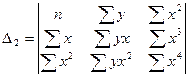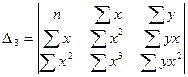В Excel определитель матрицы можно вычислить с помощью функции =МОПРЕД(числовой массив с равным количеством строк и столбцов).

Параметры уравнения регрессии равны:

; ; .

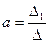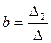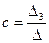Достаточно часто экономические процессы описываются гиперболой:

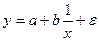или .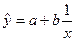

Для нахождения параметров модели a и b пользуются также МНК. Система нормальных уравнений для гиперболической зависимости имеет вид:

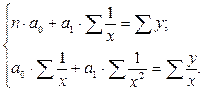
Если сделать следующую замену 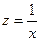, то в результате получим линейное уравнение регрессии и, соответственно, формулы для определения параметров а и b:

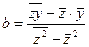и .

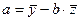Для нахождения параметров а и b в Excel можно воспользоваться функцией =ЛИНЕЙН, задавая в качестве объясняющей переменной z, а в качестве объясняемой переменной исходные значения y.

Рассмотрим примеры линеаризации некоторых моделей второго класса, т.е. нелинейных по параметрам, но внутренне линейных. Такими моделями являются степенная и показательная функции.

Для определения параметров степенной функции 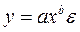(случайная ошибка мультипликативно связана с факторным признаком) с помощью МНК необходимо привести ее к линейному виду путем логарифмирования обеих частей уравнения:

.

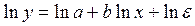Пусть 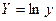; ; 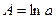; 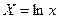, тогда уравнение степенной функции примет вид линейного уравнения 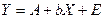или 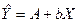, параметры которого А и b будут определяться по известным формулам:

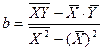и .

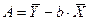Для нахождения параметров b и А можно воспользоваться функцией =ЛИНЕЙН, задавая в качестве объясняющей переменной 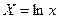, а в качестве объясняемой переменной 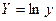, рассчитанные заранее по исходным данным х и у.

После расчетов по этим формулам сразу получаем готовый параметр b, а параметр а находим из выражения ; .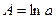

Показательная функция 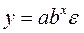, в которой ошибка 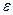мультипликативно связана с факторным признаком, также может быть подвергнута линеаризации. Для этого необходимо прологарифмировать обе части уравнения, получим:

.

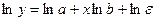Произведем следующие замены 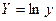; ; 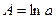; 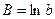, тогда уравнение примет линейный вид: 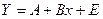, а параметры уравнения А и В могут быть определены следующим образом:

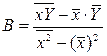и .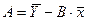

Удобно воспользоваться функцией =ЛИНЕЙН в Excel, задавая в качестве объясняющей переменной исходные значения х, а в качестве объясняемой переменной рассчитанные значения .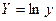

Параметры уравнения показательной функции а и b определяются следующим образом: 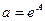и 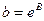. В Excel данные выражения можно вычислить с помощью функции =EXP(А).