При отборе факторов существуют определенные правила, выполнение которых необходимо.
Включение в уравнение множественной регрессии тех или иных факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями, т.е. он должен иметь определенные экономические знания, позволяющие делать вывод о наличии достаточно сильной связи между рассматриваемыми факторами и моделируемым показателем и включить эти факторы в модель. Последние должны отвечать следующим требованиям.
1. Факторы должны быть количественно измеряемы. Если в модель необходимо включить качественный фактор, не имеющий количественной меры, то ему нужно придать количественную определенность (например, качество работы маркетингового отдела фирмы задается в виде баллов, если признак альтернативный, т.е. имеющий только два значения, это могут быть значения 0 и 1).
2. Каждый фактор должен быть достаточно тесно связан с результатом (т.е. коэффициент парной линейной корреляции между каждым фактором, включаемым в модель, и результатом должен отличаться от нуля, причем на достаточно большую величину):
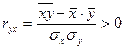
3. Факторы не должны быть тесно связаны между собой и тем более находится в строгой функциональной зависимости (не должны коррелировать друг с другом или, иначе говоря, не должны быть интеркоррелированы, интеркорреляция – связь между двумя факторами).
Существование корреляционной связи между факторами может быть выявлено с помощью показателей корреляции между ними, в частности с помощью парных коэффициентов корреляции, которые можно записать в виде матрицы линейных коэффициентов межфакторной корреляции:
| x1 | x2 | … | хp | |
| x1 | rx1x1 | rx1x2 | … | rx1xp |
| x2 | rx2x1 | rx2x2 | … | rx2xp |
| … | … | … | … | … |
| хp | rxpx1 | rxpx2 | … | rxpxp |
Коэффициент корреляции фактора с самим собой равен единицы (rxixi=1), а коэффициент корреляции фактора i c фактором j равен коэффициенту корреляции фактора j с фактором i (rxixj=rxjxi). Следовательно, данная матрица является симметричной, поэтому в ней указывается только главная диагональ и элементы под ней:
| x1 | x2 | … | хp | |
| x1 | ||||
| x2 | rx2x1 | |||
| … | … | … | ||
| хp | rxpx1 | rxpx2 | … |
Если парный линейный коэффициент корреляции между двумя признаками больше 0,7, то один из этих признаков должен быть исключен из модели. Как правило, исключается тот, чей парный коэффициент корреляции с результативным признаком меньше.
Мультиколлинеарность – связь между несколькими факторами, включенными в модель. Наличие мультиколлинеарности можно подтвердить, найдя определитель матрицы парных коэффициентов корреляции. Если связь между факторами полностью отсутствует, то определитель матрицы равен единице. Если же связь между факторами является тесной, то определитель матрицы близок к нулю. Мультиколлинеарность в эконометрических моделях необходимо избегать, поскольку она их искажает.
Причины возникновения мультиколлинеарности между признаками:
1. Изучаемые факторные признаки характеризуют одну и ту же сторону явления или процесса (например, показатели объема произведенной продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как оба характеризуют размер предприятия).
2. Использование в качестве факторов признаков, суммарное значение которых представляет собой постоянную величину (например, коэффициент годности и износа).
3. Включение в модель факторных признаков, которые являются элементами друг друга (например, затраты на производство продукции и себестоимость продукции)
4. Включение в модель факторных признаков, которые по экономическому содержанию дублируют друг друга (например, прибыль и рентабельность продукции).
Таким образом, мультиколлинеарности можно избежать еще на этапе экономического анализа изучаемого явления.
Методы устранения или уменьшения мультиколлинеарности.
1. Сравнение значений линейных коэффициентов корреляции. Из двух связанных друг с другом факторов один исключается из модели.
2. Метод включения факторов заключается в том, что в модель включаются факторы по одному в определенной последовательности. На первом шаге в модель вводится тот фактор, который имеет наибольший коэффициент корреляции с зависимой переменной. Затем поочередно добавляются другие факторы. Каждый раз оценивается целесообразность включения нового фактора с точки зрения сокращения остаточной дисперсии.
3. Метод исключения факторов состоит в том, что в модель включаются все факторы. Затем после построения уравнения регрессии из модели исключают фактор, коэффициент при котором незначим. Процесс исключения факторов продолжается до тех пор, пока модель не станет удовлетворять определенным условиям и все коэффициенты регрессии не будут значимы.
 2014-02-02
2014-02-02 5779
5779
