Туннельный эффкт

Прохождение частицы сквозь потенциальный барьер.

Рассмотрим потенциальный барьер простейшей прямоугольной формы (рис. 4, а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать

.

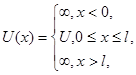
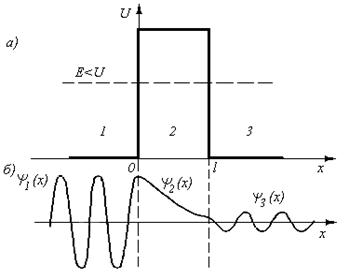
Рис. 4

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е > U), либо отразится от него (при Е < U)и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер.

Для микрочастицы даже при Е > U имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е < U имеется также отличная от нуля вероятность, что частица окажется в области х >1, т. е. проникает сквозь барьер. Подобные, выводы следуют непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при условиях данной задачи.

Уравнение Шредингера для стационарных состояний для каждой из выделенных на рис. 4, а области имеет вид

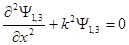(для областей 1 и 3 k²= 2mE / ħ²),

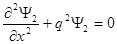(для области 2 q²= 2m (E – U) / ħ²). (1)

Общие решения этих дифференциальных уравнений:

Ψ₁(x) = A₁ ·e ^ikx + B₁ ·e ^–ikx (для области 1); (2)

Ψ₂(x) = A₂ ·e ^iqx + B₂ ·e ^{– iqx} (для области 2);

Ψ₃(x) = A₃ ·e ^ikx + B₃ ·e ^–ikx (для области 3); (3)

В выражении (2) первый член представляет собой плоскую волну, распространяющуюся в положительном направлении оси х (соответствует частице, движущейся в сторону барьера), а второй – волну, распространяющуюся в противоположном направлении, т. е. отраженную от барьера (соответствует частице, движущейся от барьера налево).

Решение (3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент В₃ в формуле (3) следует принять рапным нулю.

В области 2решение зависит от соотношений E > U или E<U. Физический интерес представляет случай, когда полная энергия частицы меньше высоты потенциального барьера, поскольку при Е<U законы классической физики однозначно не разрешают частице проникнуть сквозь барьер. В данном случае, согласно (1), q =iβ – мнимое число, где

.

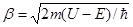Учитывая значение q и В ₃ = 0 получим решения уравнения Шредингера для трех областей в следующем виде:

Ψ₁(x) = A ₁e ^ikx + B ₁e ^{– ikx} (для области 1)

Ψ₂(x) = A₂e ^{- βx} + B ₂e ^βx (для области 2) (221.5)

Ψ₃ (x) = A ₃e ^ikx (для области 3)

В области 2 функция уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные.

Качественный вид функций Ψ₁(х), Ψ₂(х)и Ψ₃(x) показан на рис. 4, б. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей амплитудой. Следовательно, получили, что частица имеет отличную от нуля вероятность прохождения сквозь потенциальный барьер конечной ширины.

Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих

.

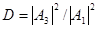Для того чтобы найти отношение | А ₃ /А ₁|²,необходимо воспользоваться условиями непрерывности Ψ и Ψ´на границах барьера х = 0и x = l (рис.4):

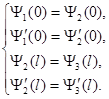(6)

Эти четыре условия дают возможность выразить коэффициенты A ₂, A ₃, В ₁и B ₂ через А ₁. Совместное решение уравнений (6) для прямоугольного потенциального барьера дает (в предположении, что коэффициент прозрачности мал по сравнению с единицей)

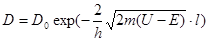, (7)

где U – высота потенциального барьера, Е – энергия частицы, l – ширина барьера, D ₀ – постоянный множитель, который можно приравнять единице. Из выражепия (7) следует, что D сильно зависит от массы т частицы, ширины l барьера и от (U – E); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

Для потенциального барьера произвольной формы (рис.5) имеем

, где U =U (x).

Cклассической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица. находясь в области барьера, должна была бы обладать отрицательной кинетической анергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Δ р на отрезке Δ х = l составляет Δ р > h / l. Связанная с этим разбросом в значениях импульса кинетическая энергия (Δ р)² / (2 т)может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной.

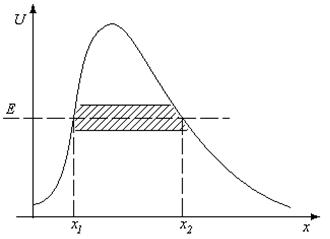
Рис. 5

Основы теории туннельных переходов заложены работами Л. И. Мандельштама и М. Л. Леонтовича (1903 – 1981). Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, α-распад, протекание термоядерных реакций).