Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится.
Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Так, ряд, показанный в примере 2, условно сходящийся. Ряд
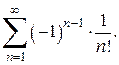
абсолютно сходится, т. к. ряд, составленный из модулей его членов, сходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Основные свойства абсолютно сходящихся рядов приводим без доказательства.
1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле).
2. Абсолютно сходящиеся ряды с суммами S1 и S2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 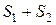 (или соответственно
(или соответственно 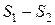 ).
).
3. Под произведением двух рядов 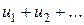 и
и  понимают ряд вида
понимают ряд вида 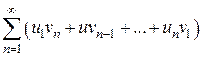
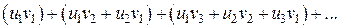
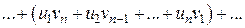
Произведение двух абсолютно сходящихся рядов с суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1· S2.
Таким образом, абсолютно сходящиеся ряды суммируются, вычитаются, перемножаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов.
В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места.
Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится. Например, ряд 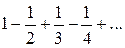 условно сходится по признаку Лейбница. Пусть его сумма равна S. Перепишем его члены так, что после одного положительного члена будут идти два отрицательных. Получим ряд
условно сходится по признаку Лейбница. Пусть его сумма равна S. Перепишем его члены так, что после одного положительного члена будут идти два отрицательных. Получим ряд
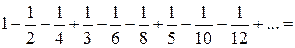
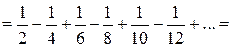
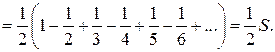
Сумма уменьшилась вдвое.
Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд (теорема Римана).
Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем.
 2014-02-02
2014-02-02 7314
7314