Код Хаффмана

Кодирование

Одно из важных приложений концепции энтропии заключается в том, что эта кон­цепция помогает понять принциды работы алгоритмов сжатия данных. Энтропия случайной переменной или источника сообщений определяет количество битов, требуемых для представления результатов случайной переменной или альтерна­тивных сообщений без потери информации. Таким образом, при разработке алго­ритма сжатия данных энтропия представляет собой меру максимально возможного.

Рассмотрим случайную переменную X, принимающую одно из восьми возможных значений (х₁,x₂, …, х₈) со следующими вероятностями:

P₁ = 0,512, Р₅ = 0,032,

Р₂ = 0,128, Р₆ = 0,032,

Р₃ = 0,128, Р₇ = 0,032,

Р₄ = 0,128, Р₈ = 0,008.

Здесь P_i представляет собой вероятность выпадения результата х_i. Предполо­жим, что сообщение состоит из реализаций случайной переменной X, и мы хотели бы закодировать сообщение в двоичном виде. Один очевидный вариант решения заключается в том, чтобы использовать 3-битовый код фиксированной длины, в котором каждое из восьми возможных значений случайной переменной X коди­руется одним 3-битовым числом. Лучшая стратегия заключается в использовании кода переменной длины, в котором более длинные кодовые слова назначаются менее вероятным значениям X, а более вероятные значения X кодируются корот­кими кодовыми словами. Такой технический прием применяется в азбуке Морзе и коде Хаффмана. Предположим, что сообщения должны передаваться при помощи алфавита из N символов. Каждый символ должен уникальным образом кодироваться двоичной последовательностью. Нас интересует способ построения оптимального кода, то есть кода, дающего в результате минимальную среднюю длину кодируемого сообще­ния. Важно отметить, что мы не ищем минимальную длину кода для какого-либо конкретного сообщения или для всех сообщений (последнее найти невозможно), но минимальную длину кода, усредненную по всем возможным сообщениям.

Другой способ взглянуть на данные требования состоит в том, что мы получа­ем сообщение, уже закодированное путем назначения символам двоичных слов фиксированной длины. Таким образом, если символов 8, каждый символ кодиру­ется тремя битами. Если число символов в алфавите от 9 до 16, то каждый символ кодируется четырьмя битами и т. д. Такое кодирование не является оптимальным, если символы встречаются в сообщениях с разной вероятностью. В этом случае требование может быть сформулировано следующим образом. Требуется разрабо­тать оптимальную схему кодирования с использованием кода переменной длины, позволяющую получить кодированное сообщение минимальной средней длины.

Рассмотрим двоичный код с кодовыми длинами L₁, L₂ …L_N, поставленный в соответствие алфавиту из N символов с вероятностями Р₁, Р₂,..., Р_N. Для удоб­ства предположим, что символы организованы в порядке убывания вероятности (P₁ >= Р₂>=... >= P_n). Можно показать, что оптимальный код должен удовлетворять следующим требованиям:

· Никакие два разных сообщения не должны состоять из одинаковых после­
довательностей битов.

· Никакое кодовое слово не должно совпадать с префиксом другого кодового
слова.

· Символы, встречающиеся с большей вероятностью, должны кодироваться более короткими кодовыми словами. То есть L₁<=L₂<=... <=L_n.

· Два кодовых слова для символов с наименьшей вероятностью должны иметь
одинаковую длину (L_N = L_n-1) и различаться только последней цифрой.

Первое требование гарантирует уникальность кодирования любого сообщения. Второе требование определяет так называемый мгновенный код. Это требование не является строго обязательным, но оно требуется, чтобы гарантировать, что сооб­щение может быть декодировано шаг за шагом. При продвижении слева направо, как только последовательность битов совпадает с данным кодовым словом, деко­дирующий алгоритм может произвести соответствующее назначение. Вот пример кода, нарушающего первые два требования:

x₁ 0

х₂ 010

х₃ 01

x₄ 10

Двоичная последовательность 010 может соответствовать одному из трех со­общений:

x ₂, x₃x₁, x₁x₄

Назначение третьего требования легко понять, если отметить, что при наруше­нии данного условия, поменяв два кода, вы сможете получить меньшее значение средней длины. Чтобы понять суть последнего требования, предположим, что L_n > L_n-1 По вто­рому требованию кодовое слово N - 1 не может быть префиксом кодового слова N. Поэтому первые N- 1 цифры кодового слова N составляют уникальное кодовое слово, а остальные цифры можно отбросить. Если эти два кодовых слова разли­чаются в каком-либо бите, кроме последнего, мы можем отбросить последний бит у каждого слова, получая таким образом лучший код.

На основании этих методов можно построить код, называемый кодом Хаффман. Начнем с упорядочивания всех символов по убыванию вероятности, так что мы получим символы (а₁, а₂,..., a_N) с вероятностями P(a₁) >=Р(а₂) >=... >=P(а_N). Затем объединим два последних символа в эквивалентный символ с вероятно­стью Р(а_N-1) + Р(а_N). Коды этих двух символов будут одинаковыми, кроме послед­них двух цифр. Теперь у нас есть новый набор из N- 1 символов. При необходи­
мости поменяем порядок следования символов таким образом, чтобы получить
символы (b₁, b₂,... b _N-1) с вероятностями P(b₁) >= P(b₂)>=... >= Р(b_N-1). Теперь мы мо­
жем повторять этот процесс до тех пор, пока не останется всего два символа. Рисунок ниже иллюстрирует этот процесс для набора символов, заданного в на­чале раздела. Будем считать каждый символ листовым узлом создаваемого дере­ва. Объединим два узла с минимальной вероятностью в узел, вероятность которого равна сумме двух соответствующих вероятностей. На каждом шаге будем повто­рять этот процесс до тех пор, пока не останется только один узел. В результате мы получим дерево, в котором у каждого узла, кроме корневого, одна ветвь отходит направо и две налево. На каждом узле пометим две левые ветви символами 0 и 1 соответственно. Для каждого символа кодовое слово представляет собой строку меток от корневого узла к исходному символу. Все получившиеся в результате ко­довые слова показаны в левой части рисунка. Для примера процесс построения кодового слова для символа x ₇ обозначен жирной линией.

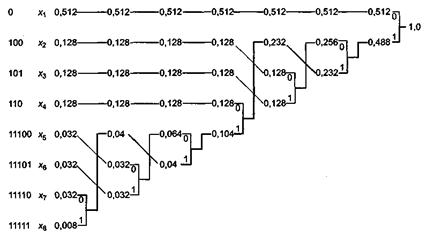
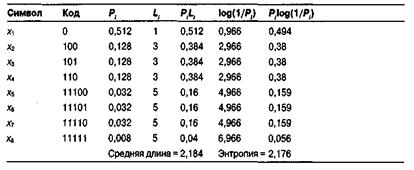
В таблице ниже приведены свойства кода Хаффмана для данного примера. Сред­няя длина кодового слова представляет собой вычисляемую следующим образом ожидаемую величину:

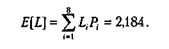
Здесь L_i представляет собой длину i-го кодового слова. Таким образом, напри­мер, для сообщений, состоящих из 1000 символов, средняя длина кодированного сообщения равна 2184 бит. При простом кодировании каждого символа тремя би­тами длина этого сообщения будет составлять 3000 бит.