Оценка погрешности зависит от длины элементарного отрезка  , и при достаточно малом
, и при достаточно малом  справедливо приближенное равенство:
справедливо приближенное равенство: 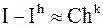 , где
, где  приближенное значение интеграла. Если уменьшить шаг
приближенное значение интеграла. Если уменьшить шаг  в два раза, то получим:
в два раза, то получим: 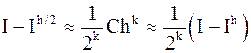 .
.
Вычитая одно из другого, получим: 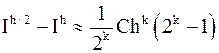 , или
, или 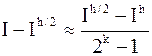 .
.
Это приближенное равенство дает оценку погрешности. Вычисление этой оценки называется правилом Рунге. Правило Рунге – это эмпирический способ оценки погрешности, основанный на сравнении результатов вычислений, проводимых с разными шагами  . Для формулы Симпсона
. Для формулы Симпсона 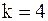 , и оценка принимает вид:
, и оценка принимает вид: 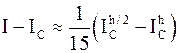 .
.
Используя правило Рунге, можно построить процедуру приближенного вычисления интеграла с заданной точностью 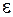 . Нужно, начав вычисления с некоторого значения шага
. Нужно, начав вычисления с некоторого значения шага  , последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение
, последовательно уменьшать это значения в два раза, каждый раз вычисляя приближенное значение 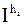 . Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на
. Вычисления прекращаются тогда, когда результаты двух последующих вычислений будут различаться меньше, чем на 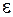 .
.
Пример. Вычислить 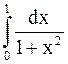 .
.
Решение. Возьмём 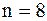 , тогда
, тогда 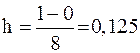 .
.
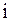 | 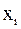 | 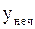 | 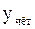 | 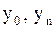 |
| 10)0,54) | ||||
| 0,125 | 0,984625 | |||
| 0,250 | 0,9411761) | |||
| 0,375 | 0,876712 | |||
| 0,5 | 0,82) | |||
| 0,625 | 0,7191 | |||
| 0,750 | 0,643) | |||
| 0,875 | 0,566389 | |||
| 3,45955 | 1,62818 | 1,5 |
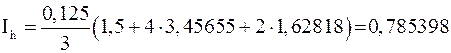 .
.
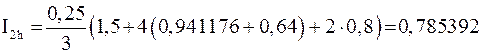 .
.
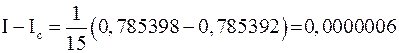 .
.
Следовательно, значение интеграла можно счесть 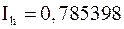 .
.
 2014-02-02
2014-02-02 14771
14771








