Будем искать многочлен в виде линейной комбинации множеств степени 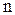 :
: 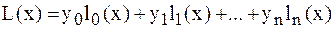 .
.
При этом потребуем, чтобы каждый многочлен 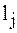
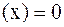 во всех узлах интерполяции, за исключением одного
во всех узлах интерполяции, за исключением одного 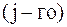 , где он равен 1. Легко проверить, что этим условиям отвечает многочлен вида
, где он равен 1. Легко проверить, что этим условиям отвечает многочлен вида
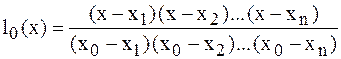 .
.
Действительно, 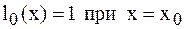 . При
. При 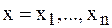 числитель выражения равен 0. По аналогии получим:
числитель выражения равен 0. По аналогии получим:
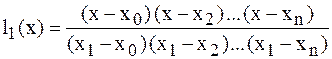 ,
,
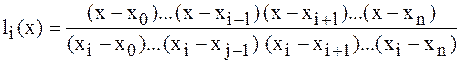 .
.
Подставив эти формулы в исходный многочлен, получим:
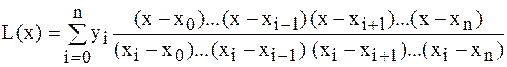 .
.
Эта формула называется интерполяционным многочленом Лагранжа.
Пример. Построить интерполяционный многочлен Лагранжа 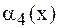 , совпадающий с функцией
, совпадающий с функцией 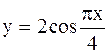 в точках
в точках 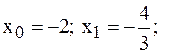
 .
.
Решение. Составим таблицу
| х | -2 | -4/3 | 4/3 | ||
| у |
Подставляя эти значения в формулу Лагранжа, получим:
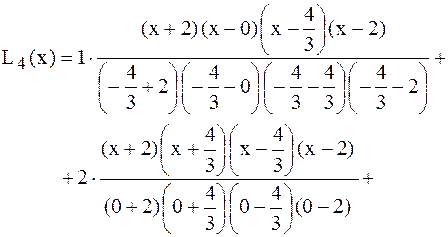
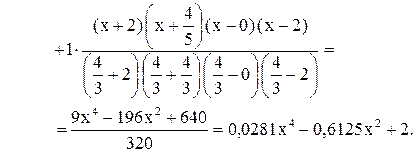
Если функция 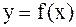 непрерывно дифференцируема до
непрерывно дифференцируема до 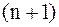 -го порядка включительно, то остаточный член интерполяционного многочлена в форме Лагранжа имеет вид
-го порядка включительно, то остаточный член интерполяционного многочлена в форме Лагранжа имеет вид
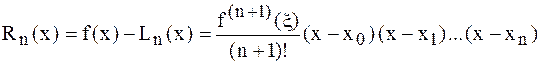 ,
,
где 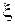 – внутренняя точка минимального отрезка, содержащего узлы интерполирования
– внутренняя точка минимального отрезка, содержащего узлы интерполирования 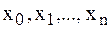 и точку
и точку 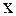 .
.
 2014-02-02
2014-02-02 1396
1396
