Рассмотрим случай равноотстоящих узлов интерполяции, т. е. 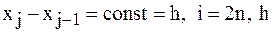 – называется шагом.
– называется шагом.
Введем понятие конечных разностей. Пусть известны значения функции в узлах 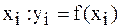 . Составим разности значений функции:
. Составим разности значений функции:
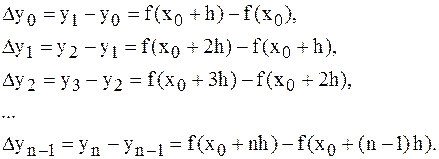
Эти разности называются разностями первого порядка.
Можно составить разности второго порядка:
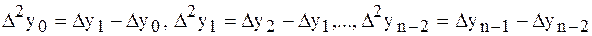 .
.
Аналогично составляются разности k-го порядка:
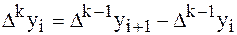 .
.
Выразим конечные разности непосредственно через значение функции:
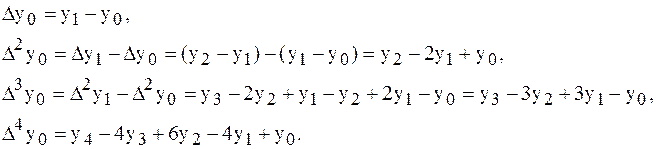
Таким образом, для любого k можно записать:
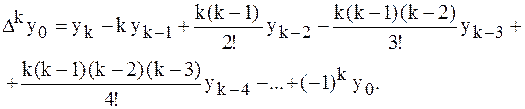
Запишем эту формулу для значений разности в узле 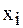 :
:
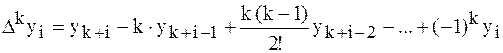 .
.
Используя конечные разности, можно определить
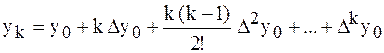 .
.
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде
|
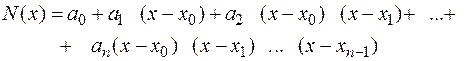
График многочлена должен проходить через заданные узлы, то есть 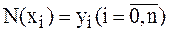 . Используем эти условия для нахождения коэффициентов многочлена:
. Используем эти условия для нахождения коэффициентов многочлена:
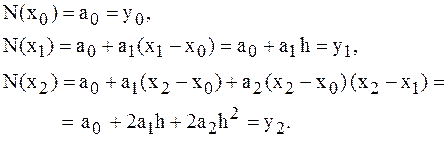
Найдем отсюда коэффициенты  :
:
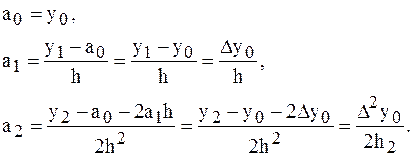
Таким образом, для любого 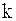 -го коэффициента формула примет вид
-го коэффициента формула примет вид
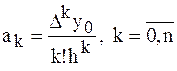 .
.
Подставляя эти формулы в выражение многочлена Ньютона, получим его следующий вид:
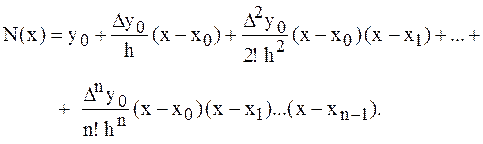
Полученную формулу можно записать в другом виде. Для этого введем переменную 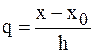 .
.
В этом случае 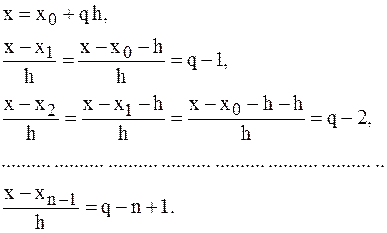
С учетом этих соотношений формулу многочлена Ньютона можно записать в виде
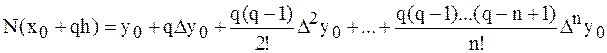 .
.
Полученное выражение может аппроксимировать данную функцию 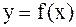 на всем отрезке изменения аргумента
на всем отрезке изменения аргумента 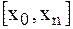 . Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем
. Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем 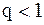 , то есть использовать эту формулу для всех
, то есть использовать эту формулу для всех 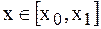 . Для других случаев вместо
. Для других случаев вместо 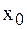 принять
принять 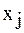 , если
, если 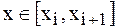 при
при 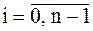 . В этом случае интерполяционный многочлен можно записать в виде
. В этом случае интерполяционный многочлен можно записать в виде

Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед. Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Это объясняется следующим: разности 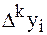 вычисляются через значения функции
вычисляются через значения функции 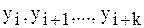 , причем
, причем 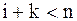 . Из-за этого при больших значениях
. Из-за этого при больших значениях 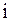 мы не можем вычислить высших порядков
мы не можем вычислить высших порядков 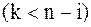 .
.
Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае 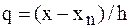 , то есть
, то есть 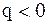 , и интерполяционный многочлен Ньютона можно получить в виде:
, и интерполяционный многочлен Ньютона можно получить в виде:
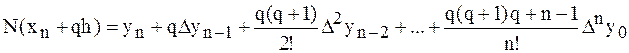 .
.
Полученная формула называется вторым интерполяционным многочленом назад.
Пример. Используя интерполяционный полином Ньютона, вычислить 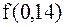 , где функция
, где функция 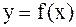 задана таблицей
задана таблицей
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| у | 0,1002 | 0,2013 | 0,8045 | 0,4108 | 0,5211 |
Решение. Составляем таблицу конечных разностей.
| х | у | 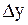 | 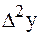 | 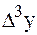 | 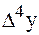 | 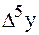 |
| 0,1002 | ||||||
| 0,1 | 0,1002 | 0,0009 | ||||
| 0,1011 | 0,0012 | |||||
| 0,2 | 0,2013 | 0,0021 | -0,0002 | |||
| 0,1032 | 0,0010 | 0,0001 | ||||
| 0,3 | 0,3045 | 0,0031 | -0,0001 | |||
| 0,1063 | 0,0009 | |||||
| 0,4 | 0,4108 | 0,0040 | ||||
| 0,1103 | ||||||
| 0,5 | 0,5211 |
Для вычисления 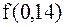 положим в интерполяционном многочлене Ньютона вперед
положим в интерполяционном многочлене Ньютона вперед 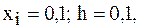 тогда
тогда 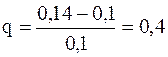 и
и
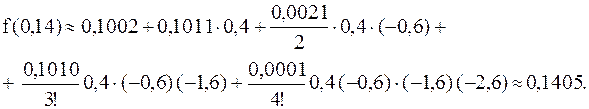
Пример. Задана таблица. Найти 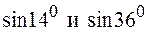 .
.
| х | 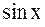 | 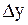 | 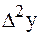 | 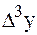 |
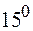 | 0,2588 | |||
| 0,0832 | ||||
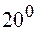 | 0,3420 | -0,026 | ||
| 0,0806 | 0,0006 | |||
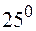 | 0,4226 | -0,032 | ||
| 0,0774 | 0,0006 | |||
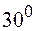 | 0,5 | 0,038 | ||
| 0,0736 | ||||
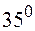 | 0,5736 |
При вычислении 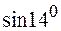 положим
положим
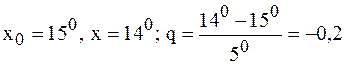 .
.
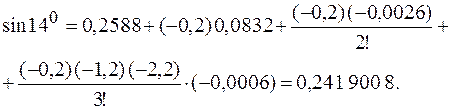
При вычислении  положим
положим
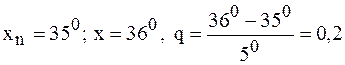 .
.
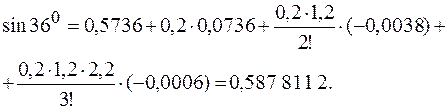
Оценим погрешности формул Ньютона вперед и назад:
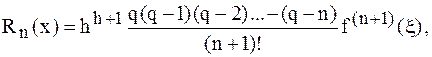 где
где 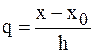 и
и
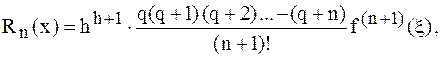 где
где 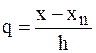 .
.
Формулы приближенного дифференцирования основаны на первой интерполяционной формуле Ньютона. Интерполяционный многочлен Ньютона имеет вид
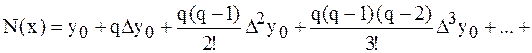 ,
,
где 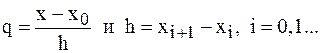
Производя перемножение биномов, получим
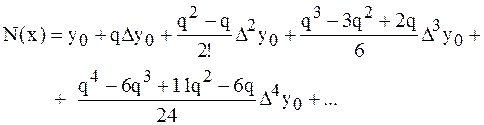
так как 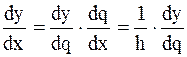 , то
, то
|

Аналогично можно вычислять производные функции любого порядка.
В некоторых случаях требуется находить производные функций 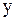 в основных табличных точках
в основных табличных точках 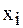 . Так как табличное значение можно считать за начальное, то положив
. Так как табличное значение можно считать за начальное, то положив 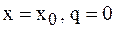 , имеем
, имеем
 ,
,
Для производной многочлена Ньютона первого порядка погрешность может быть вычислена по формуле 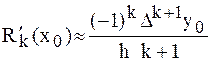 ,
,
где 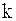 – число конечных разностей в многочлене Ньютона.
– число конечных разностей в многочлене Ньютона.
Пример. Найти 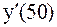 функции
функции 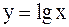 , заданной таблично.
, заданной таблично.
 2014-02-02
2014-02-02 10043
10043








