Для описания дискретных устройств наряду с булевыми функциями применяются функции, у которых аргументы и сами функции принимают значения из множества, содержащего k элементов (0,1.. k-1) [1].
Определение. Функция, принимающая значения из множества
{0,1.. k-1}, аргументы которой также принимают значения из этого множества, называется функцией k-значной логики.
Булева функция есть функция двухзначной логики. Функция
k - значной логики может быть задана таблицей истинности вида:
| x1 | x2 | ... | xn | f(x1... xn) |
| f(0,0,...,0) | ||||
| f(0,0,...,1) | ||||
| f(0,1,...,0) | ||||
| f(0,1,...,1) | ||||
| ... | ... | ... | ... | ... |
| k-1 | k-1 | k-1 | f(k-1,k-1,...k-1) |
Число k - ичных наборов длины n равно k 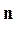 и на каждом из них значение функции может задаваться k способами, поэтому число функций k - значной логики определяется числом k
и на каждом из них значение функции может задаваться k способами, поэтому число функций k - значной логики определяется числом k 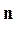 . Аналогично двузначной логике в k - значной логике выделяются элементарные функции:
. Аналогично двузначной логике в k - значной логике выделяются элементарные функции:
1. Квазиконъюнкция
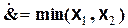
2. Квазидизъюнкция
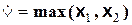
3. Сумма по модулю k
{x1Å x2}mod k
Значение функции равно остатку от деления суммы x1 + x2 на k..
4. Произведение по модулюk
{x1Äx2}mod k
Значение функции равно остатку от деления произведения x1 и x2 на k.
5. Функция Вебба, (стрелка Пирса ¯),
{max(x1, x2)+1}mod k
6. Цикл (циклическое отрицание)
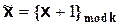
7. Функция инверсии
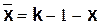 .
.
В алгебре k - значной логики действуют законы аналогичные законам булевой алгебры. Кроме того к элементарным функциям относятся следующие характеристические функции:
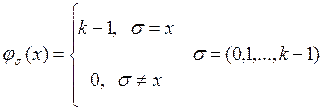
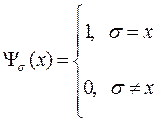 s = (0, 1,..., k-1).
s = (0, 1,..., k-1).
Построим таблицы, задающие введенные элементарные функции. В трехзначной логике f =0, f = 1, f = 2 будут представлять собой константы.
| x1 | x2 | 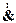 | 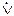 | x1 ¯ x2 | x1Å x2 | x1Ä x2 |
| x | j0 | j1 | j2 | 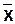 | 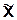 |
 2014-02-02
2014-02-02 1765
1765
