2015-04-01
1216
В число функций алгебры логики, подсчитываемых с помощью теоремы 1, входят как функции, существенно зависящие от всех п аргументов, так и функции, для которых часть из этих аргументов являются фиктивными.
Теорема 2. Число всех функций алгебры логики, существенно зависящих от п аргументов, определяется следующим рекуррентным соотношением:
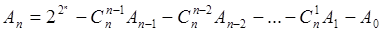
В этом соотношении Ai есть число функций алгебры логики, существенно зависящих от i аргументов. Правая часть соотношения есть разность между числом всех функций алгебры логики и суммой всех функций алгебры логики, зависящих существенно от любого числа аргументов, меньшего чем п. Справедливость приведенного соотношения очевидна.
Рассмотрим одиннадцать функций, которые играют большую роль в построении теории функций алгебры логики и ее приложениях. Эти функции мы будем называть в дальнейшем элементарными.
Рассмотрение множества элементарных функций алгебры логики начнем со случая п = 0. В силу теоремы 1 в этом случае имеются только две функции, совпадающие с константами 0 и 1: f 1 = 0, f 1 = 1. Обе эти функции мы будем считать элементарными.
|
|
|
Для п = 1, согласно теореме 1, имеем 22 = 4 различные функции, представленные в таблице 4.6.
В этом случае только функции f 3 и f 4 существенно зависят от х 1, а для функций f 1 и f 2 этот единственный аргумент является фиктивным. Эти две функции определяются таблицей 4.7.
Таблица 4.6 – Логические функции
одного аргумента
| x 1 | f 1 | f 2 | f 3 | f 4 |
Таблица 4.7 - Логические функции
повторения и отрицания
| x 1 | f 3 | f 4 |
Эти две функции мы также причислим к элементарным, будем их называть функциями повторения и отрицания и записывать следующим образом:
f 3 = x,
f 4 =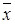 
(читается “не x ”).
Найдем число функций алгебры логики, существенно зависящих от двух и трех переменных. Из примера (таблица 4.6) вытекает, что А 0= 2 и А 1 = 2. Применяя теорему 2, имеем:
,
.
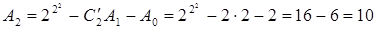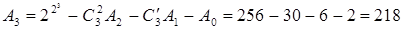В случае п = 2 в силу теоремы 2 имеем десять различных функций, существенно зависящих от аргументов х1 и х2. Из этих десяти функций к элементарным функциям будем относить следующие семь функций, представленных в таблице 4.8.
Таблица 4.8 - Элементарные логические функции двух переменных
| x 1 | x 2 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 |
Функция f 5, определяемая этой таблицей, носит название дизъюнкции х1 и х2 или логического сложения х 1 и х 2. Для ее обозначения применяются следующие символы:
f 5 (x 1, x 2) = x 1 v x 2 и f 5 (x 1, x 2) = x 1 + x 2.
Мы на протяжении всего дальнейшего изложения будем называть функцию f 5дизъюнкцией и обозначать дизъюнкцию х 1 и х2 при помощи символа "+".
Функция f 6 носит название конъюнкции или логического умножения х 1 и х 2. Для ее обозначения применяется символ "&":
|
|
|
f 6 (x 1, x 2) = x 1 & x 2.
Вместо этого символа часто применяют точку или вообще опускают всякий знак между х 1 и х 2, т. е.
f 6 (x 1, x 2) = x 1· x 2 = x 1 x 2.
В дальнейшем там, где это необходимо, будем употреблять для конъюнкции символ "&", а в остальных случаях знак между х1 и х2 будем опускать.
Функция f 7 носит название функции эквивалентности или функции равнозначности. Для ее обозначения применяется следующая запись:
f 7 (x 1, x 2) = x 1 ≡ x 2 и f 7 (x 1, x 2) = x 1 ~ x 2.
В дальнейшем будем называть эту функцию эквивалентностью х1 и х2. Для ее обозначения будем употреблять первый из двух вышеприведенных символов.
Функция f 8 носит название импликации х1 в х2. Она обозначается следующим образом:
f 8 (x 1, x 2) = x 1 → x 2.
Функция f 9 носит название функции Вебба и обозначается следующим образом:
f 9 (x 1, x 2) = x 1 О x 2.
Функция f 10 называется функцией Шеффера и обозначается следующим образом:
f 10 (x 1, x 2) = x 1 / x 2
Функция f 11 обычно называется функцией сложения по модулю два (реже ее называют функцией разноименности). Для ее обозначения употребляются символы:
f 11 (x 1, x 2) = x 1 Å x 2 и f 11 (x 1, x 2) = x 1 Δ x 2
В дальнейшем будем употреблять для обозначения функции сложения по модулю второй символ "Δ".
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедиться в том, что для этих функций имеют место:
- сочетательный закон:
x 1 & (x 2 & x 3) = (x 1 & x 2)& x 3,
x 1 + (x 2 + x 3) = (x 1 + x 2) + x 3;
- переместительный закон:
x 1 & x 2 = x 2 & x 1,
x 1 + x 2 = x 2 + x 1;
- распределительный закон конъюнкции относительно дизъюнкции:
x 1 & (x 2 + x 3) = (x 1 & x 2) + (x 1 & x 3).
Кроме того, имеет место распределительный закон дизъюнкции относительно конъюнкции:
x 1 + (x 2 & x 3) = (x 1 + x 2) & (x 1 + x 3),
который не имеет места в обычной алгебре, так как если бы он существовал, то он бы имел следующий вид:
a +b c = (a + b) (a + c).
Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения (таблица 4.9).
Совпадение в обеих результирующих частях построенной таблицы доказывает наше утверждение.
Таблица 4.9 – Сравнение логических функций
| x 1 | x 2 | x 3 | x 2 & x 3 | x 1 + (x 2 & x 3) | x 1 | x 2 | x 3 | x 1 + x 2 | x 1 + x 3 | (x 1 + x 2) & (x 1 + x 3) |
Рассмотрим теперь ряд простых, но весьма важных соотношений:
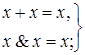| (4.10) |
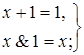| (4.11) |
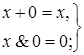| (4.12) |
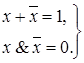| (4.13) |
Из (4.10) как следствие получаем:
x + x + …+ x = x,
x & x & …& x = x.
Как обобщение вышеприведенных формул получаем следующие формулы, обычно называемые формулами де Моргана:
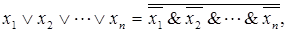| (4.14) |
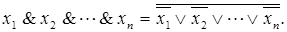| (4.15) |
Рассмотренные 11 функций позволяют строить новые функции алгебры логики двумя основными путями:
1) путем перенумерации аргументов;
2) путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f 1, f 2, …, f k и путем применения (возможно многократного) этих двух правил, будем называть суперпозицией функций f 1, f 2, …, fk..
Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить другие функции алгебры логики, являющиеся суперпозициями этих функций. Используя таблицы состояния (истинности), можно задавать в них любую функцию.
