План лекции:
1.Детерминированные и случайные функции.
2.Основные вероятностные характеристики случайных процессов.
3.Рекомендуемая литература [9].
8.1. Детерминированные и случайные функции
До сих пор поведение САУ исследовалось при определенных, заданных во времени управляющих и возмущающих воздействиях (ступенчатая функция, импульсная функция, гармоническое воздействие и т.д.). При этих условиях состояние системы может быть точно предсказано для любого момента времени заранее. Система полностью определена и называется в этом смысле детерминированной.
Однако во многих случаях характер воздействия бывает таким, что его нельзя считать определенной функцией времени. Воздействие может принимать с течением времени самые разнообразные случайные значения. В таких случаях мы можем оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени. Это происходит потому, что сама природа реального управляющего или возмущающего воздействия такова, что его величина в каждый момент времени и процесс его изменения с течением времени зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом.
Строго оптимальное поведение системы при наличии случайных воздействий неосуществимо. Однако можно говорить о наиболее вероятном приближении к тому или иному оптимуму. Обычно при этом приходится идти на определенный компромисс.
Случайная функция отличается от регулярной тем, что мы не можем утверждать, что она в данный момент времени будет иметь определенное значение. Мы можем говорить лишь о вероятности того, что в данный момент t=t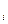 значение функции x(t
значение функции x(t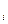 ) заключается между значениями x и x+
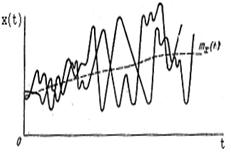
) заключается между значениями x и x+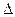 x. Понятие случайной функции – это обобщенное понятие, и говорить о значении функции в данный момент мы, в сущности, не можем. Однако в конкретно наблюдаемой кривой случайного процесса эти значения существуют. Конкретно наблюдаемая кривая случайного процесса называется реализацией случайной функции. Реализации могут иметь и определенные значения, и определенные производные (рис.8.1). Множество различных реализаций и обобщается понятием “случайная функция”.
x. Понятие случайной функции – это обобщенное понятие, и говорить о значении функции в данный момент мы, в сущности, не можем. Однако в конкретно наблюдаемой кривой случайного процесса эти значения существуют. Конкретно наблюдаемая кривая случайного процесса называется реализацией случайной функции. Реализации могут иметь и определенные значения, и определенные производные (рис.8.1). Множество различных реализаций и обобщается понятием “случайная функция”.
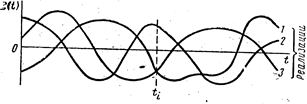
Рис. 8.1. Отдельные реализации случайной функции времени
Если график семейства реализаций случайной функции рассечь вертикальной линией, то получим случайную величину x(ti) для заданного момента времени ti.
8.2. Основные вероятностные характеристики
случайных процессов
8.2.1. функция распределения и плотность вероятности
Для характеристики случайной функции служат функции распределения вероятности и плотности вероятности.
Под функцией распределения вероятности, часто называемой интегральным законом распределения, понимают вероятность того, что случайная величина примет значение меньше некоторого фиксированного значения.
Производная от функции распределения вероятности носит название плотности вероятности или дифференциального закона распределения.
Одномерная функция распределения вероятности относится только к одному какому-либо сечению случайной функции:
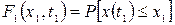 (8.1)
(8.1)
Она показывает вероятность того, что текущее значение случайной функции x(t) в момент времени t=t1 меньше заданной величины х 1.
Соответственно, одномерная плотность вероятности p1(x1,t1) есть производная от интегрального распределения вероятности F1(x1,t1) и имеет вид:
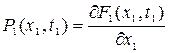 . (8.2)
. (8.2)
Величина 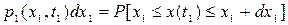 выражает вероятность того, что случайная функция x(t) в момент времени t=t1 находится в интервале от x
выражает вероятность того, что случайная функция x(t) в момент времени t=t1 находится в интервале от x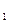 до
до 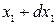 .
.
Рассмотрим теперь всевозможные пары значений х, полученные в два разных момента времени: t1 и t2. Двумерное распределение вероятности имеет вид:
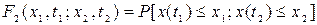 . (8.3)
. (8.3)
Двумерное распределение вероятности относится к двум произвольным сечениям x(t1), x(t2) случайной функции и выражает вероятность того, что в момент времени t1 случайная функция x(t) меньше х1, а в момент t2 — меньше х2. Соответствующая двумерная плотность вероятности имеет вид
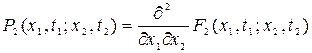 . (8.4)
. (8.4)
Некоторые типы случайных процессов полностью характеризуются одномерными или двумерными плотностями вероятности. Например, так называемый чисто случайный процесс или «белый шум» полностью характеризуется одномерной плотностью вероятности.
Значения x(t) в этом процессе, взятые в различные моменты времени t1, t2,..., совершенно независимы друг от друга. Вероятность совпадения событий, заключающихся в нахождении x(t) между х1 и 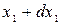 в момент t=t1 и между x2 и
в момент t=t1 и между x2 и 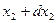 в момент t=t2 равна произведению вероятностей каждого из этих событий. Поэтому
в момент t=t2 равна произведению вероятностей каждого из этих событий. Поэтому
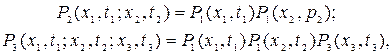 (8.5)
(8.5)
т. е. все плотности вероятности определяются одномерными плотностями.
Примером процесса, полностью характеризуемого двумерной плотностью вероятности, служит Марковский случайный процесс. Это такой процесс, для которого вероятность нахождения x(t) в заданном интервале (xn, xn+dxn) в момент t=tn , зависит только от состояния в предшествующий момент tn-1 и совершенно не зависит от состояния в другие моменты времени, т.е. от более глубокой предыстории.
Стационарный случайный процесс есть аналог установившегося процесса в детерминированной системе. Статистический характер стационарного процесса неизменен во времени.
В строгом смысле стационарным случайным процессом называют такой процесс, в котором функции распределения всех порядков не зависят от положения начала отсчета времени, т.е.
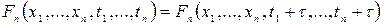
(8.6)
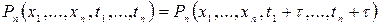
Из этих соотношений следует, что одномерные функция распределения и плотность вероятности стационарного процесса вообще не зависят от времени т.е.
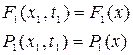 (8.7)
(8.7)
Функции распределения и плотности вероятности второго порядка для стационарного случайного процесса при одинаковых x1 и x2 остаются неизменными, если разность рассматриваемых моментов времени 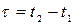 постоянна:
постоянна:
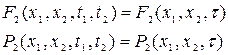 (8.8)
(8.8)
Для оценки точности линейных САУ при решении многих прикладных задач достаточно знать первые два момента процесса: математическое ожидание и корреляционную функцию. Эти характеристики являются неслучайными функциями или величинами и представляют собой результат вероятностного усреднения различных функций случайных процессов.
Свойства стохастических процессов, определяемые двумя первыми моментами, изучаются с помощью корреляционной теории. Кроме корреляционного анализа, основанного на прямом рассмотрении случайных сигналов во времени, существует также метод, основанный на рассмотрении частотных составляющих случайных сигналов, спектральный анализ. Корреляционный и спектральный анализы широко используются в инженерной практике.
8.2.2. Математическое ожидание, дисперсия
и корреляционная функция случайного процесса
Зная одномерное распределение вероятности, можно определить математическое ожидание m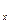 (t) случайной функции x(t) или одномерный момент первого порядка:
(t) случайной функции x(t) или одномерный момент первого порядка:
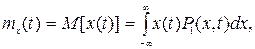 (8.9)
(8.9)
где P1 (x, t) — плотность вероятности, x(t) — случайная функция.
Математическим ожиданием или средним (по множеству) значением случайной функции x(t) называют среднеарифметическое значение бесконечного множества реализаций, т. е. это такая неслучайная функция mx(t), вокруг которой группируются все реализации данного случайного процесса и которая полностью определяется одномерным законом распределения.
Разность 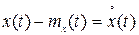 называют центрированной случайной функцией.
называют центрированной случайной функцией.
Математическое ожидание центрированной случайной функции тождественно равно нулю:
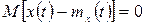 .
.
В дальнейшем будем рассматривать только центрированные случайные функции и кружочек над х опускается.
Практически математическое ожидание может быть определено по реализациям. Для этого фиксируется значение аргумента t. Тогда при t=t1 значение реализаций x1(t1), x2(t1),..., xN (t1) представляет собой обычную случайную величину. Математическое ожидание случайной величины находим как среднеарифметическое значение:
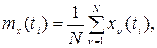 (8.10)
(8.10)
где i = 1, 2,..., n – фиксированное значение времени; 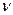 = 1, 2,…, N - номер реализации.
= 1, 2,…, N - номер реализации.
На основании подсчета, проведенного для различных t=ti, можно построить график mx(ti).
Среднее значение не полностью характеризует случайный процесс. При равных средних значениях процессы могут иметь различные отклонения. Поэтому для характеристики случайного процесса вводится понятие дисперсии.
Дисперсией случайной функции x(t) называют неслучайную и неотрицательную функцию аргумента t, представляющую собой среднее значение квадрата разности между случайной функцией и ее средним значением, или среднее значение квадрата отклонения случайной функции от ее среднего значения.
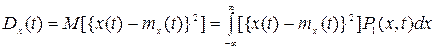 . (8.11)
. (8.11)
Она характеризует интенсивность отклонений относительно среднего значения и, так же как математическое ожидание, определяется одномерным законом распределения. Размерность дисперсии равна квадрату размерности случайной величины. Дисперсия регулярной функции равна нулю.
Среднеквадратическое отклонение равно корню квадратному из дисперсии:
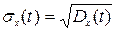 . (8.12)
. (8.12)
Введенные понятия иллюстрируются рис. 8.2. Математическое ожидание случайного процесса x(t) представляет собой некоторую среднюю кривую, около которой располагаются все возможные отдельные реализации этого процесса, а дисперсия Dx(t) или среднеквадратическое отклонение 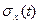 характеризует рассеяние отдельных возможных реализаций около этой средней кривой. В общем случае среднеквадратическое отклонение меняется с течением времени. Указанные характеристики m
характеризует рассеяние отдельных возможных реализаций около этой средней кривой. В общем случае среднеквадратическое отклонение меняется с течением времени. Указанные характеристики m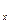 (t) и D
(t) и D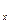 (t) для каждого данного момента времени являются средними по множеству.
(t) для каждого данного момента времени являются средними по множеству.
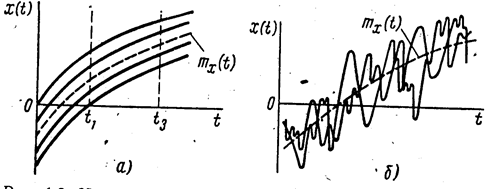
Рис. 8.2. Изменение среднего значения и отдельных реализаций
случайного процесса:
а - при сильной связи между значениями случайной функции;
б - при слабой связи
При обработке результатов испытаний дисперсия случайной функции рассчитывается по реализациям с помощью формулы
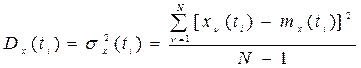 . (8.13)
. (8.13)
Для случайной функции одномерное распределение вероятности и получаемые на ее основе характеристики (математическое ожидание и дисперсия) еще не являются достаточными для оценки случайного процесса во времени.
Необходимо установить связь между значениями случайного процесса в разные моменты времени. На рис. 8.2 приведены реализации двух случайных функций, которые имеют равные математические ожидания и дисперсии, но по характеру отличаются друг от друга. Если случайная функция (см. рис. 8.2, а) при некотором t приняла значение, лежащее выше m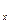 (t), то можно утверждать, что и ближайшее значение реализации случайной функции пройдет выше m
(t), то можно утверждать, что и ближайшее значение реализации случайной функции пройдет выше m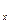 (t). Во втором случае (рис. 8.2, б) этого может и не быть. Значит, разница между рассматриваемыми случайными функциями проявляется в характере связи между значениями случайной функции для различных аргументов t1 и t2.
(t). Во втором случае (рис. 8.2, б) этого может и не быть. Значит, разница между рассматриваемыми случайными функциями проявляется в характере связи между значениями случайной функции для различных аргументов t1 и t2.
Зная двумерную функцию распределения p2(x1,t1;x2,t2), можно определить не только математическое ожидание mx(t) и дисперсию D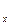 (t), но и момент второго порядка, характеризующий связь между значениями случайной функции в различные моменты времени.
(t), но и момент второго порядка, характеризующий связь между значениями случайной функции в различные моменты времени.
Математическое ожидание произведения значений центрированной случайной функции, взятых при двух моментах времени t1 и t2 называют корреляционной или автокорреляционной функцией:
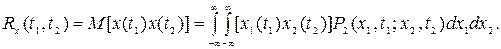 (8.14)
(8.14)
В этом выражении P2(x1,t1;x2,t2) определяет вероятность того, что в момент времени t1 значение случайного процесса находится в пределах 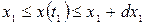 , а в момент времени t2 —в пределах
, а в момент времени t2 —в пределах 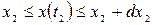 .
.
Если аргументы корреляционной функции равны между собой (t1=t2=t), то
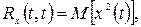 (8.15)
(8.15)
т. е. корреляционная функция для одного и того же сечения равна математическому ожиданию квадрата случайной функции. Для центрированной функции x(t) при t1=t2=t будем иметь
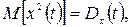
т. е. корреляционная функция равна дисперсии случайной функции.
Для характеристики статистической взаимосвязи различных случайных функций, действующих на одну и ту же систему, пользуются понятиями совместного распределения вероятности и взаимной корреляционной функции. Для функций f(t) и 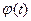 совместная функция распределения вероятности имеет вид
совместная функция распределения вероятности имеет вид
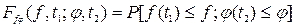 . (8.16)
. (8.16)
и означает вероятность того, что в момент времени t=t1 значение f(t1) меньше f, а в момент времени t=t2 значение 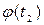 меньше
меньше 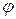 . Совместная плотность вероятности
. Совместная плотность вероятности
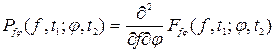 . (8.17)
. (8.17)
Соответственно взаимной корреляционной функцией двух случайных центрированных функций f и 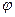 называется математическое ожидание произведения этих функций, взятых при различном времени:
называется математическое ожидание произведения этих функций, взятых при различном времени:
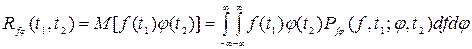 . (8.18)
. (8.18)
Случайные функции называют коррелированными, если их взаимная корреляционная функция не равна тождественно нулю, и некоррелированными при равенстве ее нулю.
8.3. Стационарные случайные процессы.
Эргодическая гипотеза
Лекция 23
План лекции:
1. Стационарные случайные процессы.
2. Эргодические случайные процессы.
3. Рекомендуемая литература [9].
8.3.1. Стационарные случайные процессы
Различные случайные процессы по степени зависимости их статистических характеристик от времени делят на стационарные и нестационарные.
Наиболее просто осуществляется анализ случайных процессов, статистические характеристики которых не зависят от текущего времени. Такие процессы называют стационарными.
Реальные физические процессы в большей или меньшей степени приближаются к стационарным процессам. Многие из них, например тепловые шумы, можно с большой точностью считать стационарными. К стационарным относятся также колебания самолета относительно установившегося горизонтального полета, шумы в радиоэлектронной аппаратуре, качка корабля и др.
Ко многим нестационарным процессам применяют результаты, полученные при исследовании стационарных процессов. Практически анализу подвергаются только обладающие конечной длительностью отрезки реализаций, и если на этих отрезках времени исследуемые процессы мало отличаются от стационарных, то к ним можно применять теорию стационарных процессов.
Различают стационарность в узком и широком смысле.
Стационарным в узком смысле называют процесс x(t), если его n -мерная плотность вероятности при любом n зависит только от величины интервалов t2 - t1,...,t n - t1 и не зависит от положения этих интервалов в области изменения аргумента t.
Стационарным в широком смысле называют процесс x(t), математическое ожидание которого постоянно:
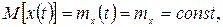 (8.19)
(8.19)
а корреляционная функция Rx(t1,t2) зависит только от разности 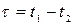 ; при этом корреляционную функцию обозначают
; при этом корреляционную функцию обозначают
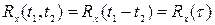 . (8.20)
. (8.20)
а)
б)
|

в)

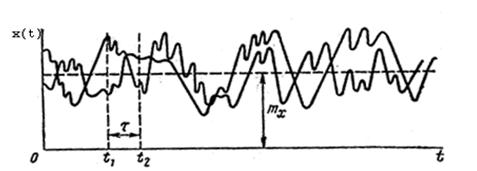
Рис. 8.3. Графики случайного процесса:
а — стационарного; б — нестационарного;
в—стационарного, но не эргодического
Для стационарного процесса x(t) дисперсия
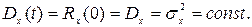
При изучении стационарных процессов можно ограничиваться процессами с математическим ожиданием, равным нулю, так как случайный процесс с ненулевым математическим ожиданием представляют как сумму процесса с нулевым математическим ожиданием и постоянной неслучайной величиной математического ожидания.
На рис. 8.3, а математическое ожидание для стационарного случайного процесса показано в виде горизонтальной прямой mx = const в отличие от общего случая, приведенного на рис. 8.3, б. Рассеяние значений переменной x(t), характеризуемое величиной 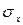 , также все время одинаково.
, также все время одинаково.
Выполнение условий (8.19) и (8.20) может служить проверкой стационарности случайного процесса.
8.3.2. Эргодические случайные процессы
Существуют стационарные процессы, которые обладают свойством эргодичности: статистические характеристики, полученные осреднением по времени одной реализации (в достаточно большом интервале наблюдения), приближенно совпадают с характеристиками, полученными осреднением по множеству реализаций (при фиксированном времени). Это положение основано на том, что раз статистические характеристики стационарного случайного процесса с течением времени не меняются, то наблюдение случайного процесса на одном объекте в течение длительного времени дает в среднем такую же картину, как незначительное число наблюдений, проведенных в один и тот же момент времени на большом числе объектов одного типа. Иными словами, отдельная реализация процесса на бесконечном промежутке времени полностью определяет весь случайный процесс с его бесчисленными реализациями. Следовательно, для определения статистических характеристик можно ограничиться одним опытом, проводимым в течение достаточно большого интервала времени, т. е. ограничиться обработкой одной реализации вместо множества опытов, необходимых для определения характеристик процесса, не обладающего свойствами эргодичности. Стационарная случайная функция x(t) эргодична, если ее корреляционная функция 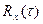 неограниченно убывает по модулю при
неограниченно убывает по модулю при 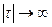 .
.
Свойство эргодичности весьма важно для решения практических задач. Многие стационарные случайные процессы, встречающиеся на практике, обладают свойством эргодичности.
Основные статистические характеристики стационарной случайной функции x(t), обладающей эргодическим свойством, определяются следующими выражениями. Математическое ожидание, или среднее значение имеет вид

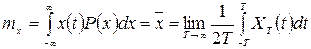 , (8.21)
, (8.21)
где 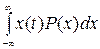 - усреднение по множеству реализаций;
- усреднение по множеству реализаций;
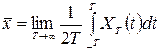 - усреднение по времени одной реализации (при достаточно большом Т),
- усреднение по времени одной реализации (при достаточно большом Т),
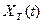 — реализация стационарного случайного процесса, взятого на интервале -T<=t<=T, а вне этого интервала равная нулю.
— реализация стационарного случайного процесса, взятого на интервале -T<=t<=T, а вне этого интервала равная нулю.
Выражение (8.21) означает, что для процесса, обладающего эргодическими свойствами, среднее по множеству реализаций равно среднему по времени для одной реализации. Чем больше интервал -T<=t<=T, тем точнее можно определить математическое ожидание. Дисперсия случайной функции
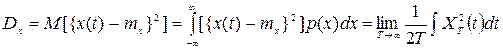 . (8.22)
. (8.22)
Корреляционная функция, характеризующая связь между значениями случайной функции в моменты x(t) и 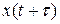 , может быть определена для стационарного эргодического процесса по одной его реализации, как среднее по времени от произведения случайных функций x(t) и
, может быть определена для стационарного эргодического процесса по одной его реализации, как среднее по времени от произведения случайных функций x(t) и 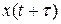 , сдвинутых относительно друг друга на определенный промежуток времени
, сдвинутых относительно друг друга на определенный промежуток времени 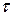 (рис. 8.3):
(рис. 8.3):
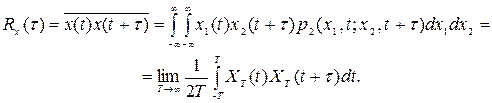 (8.24)
(8.24)
Если 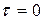 , то корреляционная функция равна дисперсии случайной функции:
, то корреляционная функция равна дисперсии случайной функции:
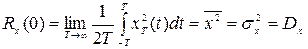 . (8.25)
. (8.25)
Корреляционная функция является более общей характеристикой случайного процесса, чем дисперсия, так как дисперсия отображает только начальную ординату графика корреляционной функции. Для многих случайных процессов при очень малых 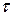 вероятность того, что значение функции
вероятность того, что значение функции 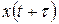 мало отличается от значения
мало отличается от значения 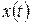 , близка к единице, т.е. близка к достоверности. По мере увеличения
, близка к единице, т.е. близка к достоверности. По мере увеличения 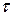 , связь между значениями x(t) и
, связь между значениями x(t) и 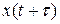 ослабевает, они делаются взаимно независимыми, и функция
ослабевает, они делаются взаимно независимыми, и функция 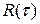 стремится к нулю.
стремится к нулю.
Для оценки свойств корреляционных функций иногда вводят понятие времени корреляции. Интервал между двумя сечениями x(t) и 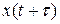 , начиная с которого можно практически считать некоррелированными случайные величины x(t) и
, начиная с которого можно практически считать некоррелированными случайные величины x(t) и 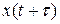 , называют временем корреляции
, называют временем корреляции 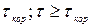 . Иными словами время корреляции - это отрезок на оси
. Иными словами время корреляции - это отрезок на оси 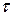 ,за пределами которого корреляционная функция R(
,за пределами которого корреляционная функция R(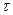 ) практически равна нулю. На рис.8.4 приведена корреляционная функция сигнала на входе системы автосопровождения цели. В последнем случае по оси ординат на графике отложено нормированное значение корреляционной функции
) практически равна нулю. На рис.8.4 приведена корреляционная функция сигнала на входе системы автосопровождения цели. В последнем случае по оси ординат на графике отложено нормированное значение корреляционной функции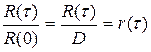 .
.
Нормализация позволяет сопоставлять 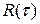 независимо от того, равны или отличаются среднеквадратические значения. Очевидно, что
независимо от того, равны или отличаются среднеквадратические значения. Очевидно, что 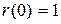 и
и 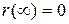 . Время корреляции
. Время корреляции 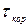 может быть нормированной корреляционной функции
может быть нормированной корреляционной функции 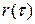 становятся при
становятся при 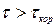 меньше достаточно малого числа, например 0,05.
меньше достаточно малого числа, например 0,05.
Взаимная корреляционная функция двух случайных, но взаимно зависимых процессов определяется по формуле
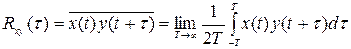 . (8.26)
. (8.26)
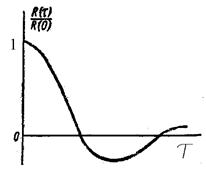
Рис. 8.4. Примерный вид нормированной корреляционной функции
флуктуации, отраженных от цели сигналов
Для статистически независимых процессов x и y взаимная корреляционная функция равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения). Общей же силы обратный вывод не имеет.
Лекция 24
План лекции:
1.Спектральная плотность стационарного эргодического процесса.
2.Свойства корреляционных функций и спектральных
плоскостей стационарного эргодического процесса.
4. Рекомендуемая литература [9].
8.4. Спектральная плотность стационарного
эргодического случайного процесса
При статистическом анализе САУ для стационарных случайных функций удобно пользоваться спектральной плотностью случайной функции, т. е. изображением Фурье корреляционной функции:
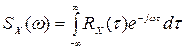 , (8.27)
, (8.27)
где 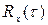 является оригиналом, а
является оригиналом, а 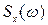 изображением Фурье. Учитывая, что
изображением Фурье. Учитывая, что 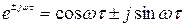 , а
, а 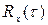 и
и 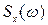 вещественные четные функции, получим
вещественные четные функции, получим
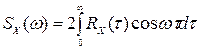 . (8.28)
. (8.28)
Спектральная плотность является положительной функцией во всем диапазоне частот от 0 до 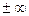 . Как и сама корреляционная функция, она не содержит сведений о фазах отдельных гармонических составляющих.
. Как и сама корреляционная функция, она не содержит сведений о фазах отдельных гармонических составляющих.
Если известна спектральная плотность случайной функции, то, пользуясь обратным преобразованием Фурье, можно получить корреляционную функцию
 . (8.29)
. (8.29)
С помощью соотношений (8.27) и (8.29) можно определить спектральную плотность 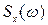 по заданной аналитически или в виде графика корреляционной функции
по заданной аналитически или в виде графика корреляционной функции 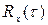 или наоборот - корреляционную функцию
или наоборот - корреляционную функцию 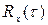 по заданной спектральной плотности.
по заданной спектральной плотности.
Спектральная плотность может быть получена и непосредственно по реализации без предварительного вычисления корреляционной функции. Взаимное преобразование Фурье
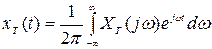 ,
,
где 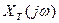 - текущий спектр процесса x
- текущий спектр процесса x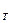 (t).
(t).
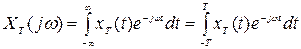 ,
,
связывает между собой вещественную функцию времени x(t) и комплексную функцию частоты 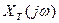 , модуль которой
, модуль которой 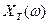 называют спектральной плотностью амплитуд или амплитудной спектральной плотностью. Последняя позволяет получить величину
называют спектральной плотностью амплитуд или амплитудной спектральной плотностью. Последняя позволяет получить величину 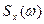 (см. формулу (8.32)).
(см. формулу (8.32)).
Физический смысл спектральной плотности может быть понятен из следующих рассуждений.
Средняя мощность стационарного процесса, например, в виде электрического тока, выделяемого на сопротивлении в 1 Ом, за время 2 T может быть выражена формулой
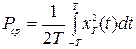 (8.30)
(8.30)
Если увеличивать интервал наблюдения 2Т до бесконечных пределов, то от интегрирования по времени можно перейти к интегрированию по спектру (см. формулу Парсеваля) [9]:
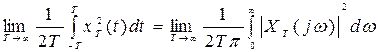 . (8.31)
. (8.31)
Внесем операцию определения предела в правой части под знак интеграла и введем обозначение подынтегральной функции:
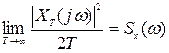 . (8.32)
. (8.32)
Подставляя (8.32) в соотношение (8.31), получим
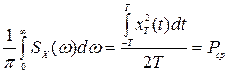 . (8.33)
. (8.33)
Интеграл в левой части характеризует мощность вовсем возможном диапазоне частот. Поэтому каждая элементарная составляющая вида 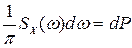 соответствует мощности в бесконечно узкой полосе частот d
соответствует мощности в бесконечно узкой полосе частот d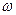 , а коэффициент
, а коэффициент 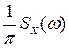 - крутизне нарастания мощности по частоте:
- крутизне нарастания мощности по частоте:
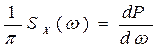 , (8.34)
, (8.34)
или плотности мощности в спектре.
В отличие от амплитудной спектральной плотности 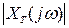 , определяющей плотность амплитуд составляющих на участке спектра
, определяющей плотность амплитуд составляющих на участке спектра 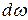 , спектральная плотность
, спектральная плотность 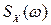 характеризует распределение мощности составляющих в интервале частот
характеризует распределение мощности составляющих в интервале частот 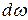 .
.
Размерность спектральной плотности [ x2 * с ], где х - размерность процесса. Иногда записывают приближенно
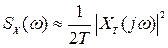 . (8.35)
. (8.35)
Если случайные процессы x(t) и y(t) стационарны и стационарно связаны, то их взаимная спектральная плотность
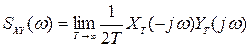 , (8.36)
, (8.36)
где 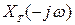 - функция, комплексно сопряженная с функцией
- функция, комплексно сопряженная с функцией 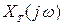 .
.
8.5. Свойства корреляционных функций и спектральных плотностей стационарных эргодических
случайных процессов
1. Начальное значение Rх (0) корреляционной функции 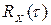 всегда превышает ее значение в любой другой момент
всегда превышает ее значение в любой другой момент 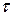 :
:
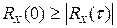 , причем
, причем 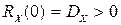 .
.
2. Предельное значение корреляционной функции при 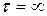 равно квадрату математического ожидания:
равно квадрату математического ожидания:
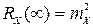 .
.
Это означает, что в бесконечно удаленные друг от друга моменты времени значения случайной функции можно считать независимыми и корреляционная функция будет отличаться от 0 только за счет присутствия детерминированной постоянной составляющей в виде математического ожидания m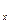 . Для центрированного случайного процесса
. Для центрированного случайного процесса
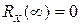 .
.
3. Корреляционная функция 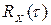 стационарного случайного процесса есть четная функция
стационарного случайного процесса есть четная функция 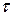 :
:
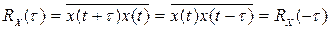 . (8.37)
. (8.37)
Поэтому корреляционная функция всегда симметрична относительно оси ординат.
Корреляционная функция симметрична относительно переменных t1, t2,
т. е.
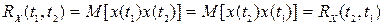 . (8.38)
. (8.38)
4. Если случайная функция содержит периодическую составляющую, то корреляционная функция также содержит периодическую составляющую той же частоты. Например, для регулярной функции 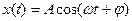 получим
получим
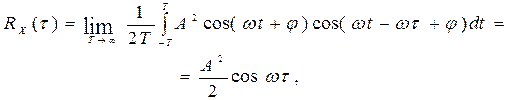 (8.39)
(8.39)
т. е. корреляционная функция синусоидальной функции представляет собой косинусоиду и не зависит от сдвига фазы (рис. 8.5, а).
5. Кривая корреляционной функции 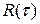 , характеризующая отраженные от подвижного объекта сигналы, располагается тем круче, чем менее инерционен объект. Например, для маневрирующего самолета связь между последующими и предыдущими положениями будет тем слабее, чем он легче и маневреннее. Можно сказать, что корреляционная функция характеризует инерционность системы, находящейся под воздействием случайных возмущений. Чем быстрее убывает
, характеризующая отраженные от подвижного объекта сигналы, располагается тем круче, чем менее инерционен объект. Например, для маневрирующего самолета связь между последующими и предыдущими положениями будет тем слабее, чем он легче и маневреннее. Можно сказать, что корреляционная функция характеризует инерционность системы, находящейся под воздействием случайных возмущений. Чем быстрее убывает 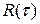 , тем более высокие частоты будут содержаться в случайном процессе.
, тем более высокие частоты будут содержаться в случайном процессе.
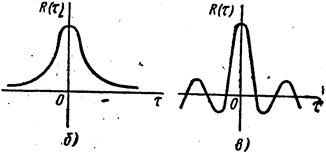 |
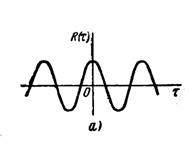 |
6. Случайный процесс без периодической составляющей имеет кривую корреляционной функции вида рис. 8.5, б, а с периодической составляющей - вида рис. 8.5, в.
Рис. 8.5. Кривые корреляционных функций:
а—периодического процесса; б—случайного процесса без периодической
составляющей, в — случайного процесса с периодической составляющей
7. Если случайная функция содержит постоянную составляющую а, то корреляционная функция—постоянную составляющую а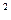 (см. формулу 8.24).
(см. формулу 8.24).
Найденные выражения для 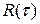 и
и 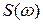 позволяют отметить следующие свойства стационарных спектральных плотностей:
позволяют отметить следующие свойства стационарных спектральных плотностей:
1. Если 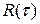 — монотонная убывающая функция от
— монотонная убывающая функция от 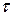 , то
, то 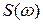 тоже монотонная убывающая функция.
тоже монотонная убывающая функция.
2. Чем шире график корреляционной функции 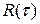 , тем уже график спектральной плотности
, тем уже график спектральной плотности 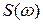 . Это соответствует физической сущности процесса: чем медленнее процесс, тем меньше значение в процессе имеют высокие частоты.
. Это соответствует физической сущности процесса: чем медленнее процесс, тем меньше значение в процессе имеют высокие частоты.
Например, для случайного стационарного процесса с экспоненциально затухающей корреляционной функцией 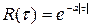
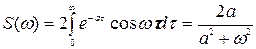 . (8.40)
. (8.40)
3. Если 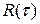 стремится к нулю в течение очень короткого промежутка времени
стремится к нулю в течение очень короткого промежутка времени 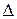 , то
, то 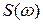 сохраняет приблизительно постоянное значение. Такой спектр называют белым.
сохраняет приблизительно постоянное значение. Такой спектр называют белым.
4. Для постоянной составляющей 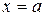 корреляционная функция
корреляционная функция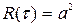 , а график спектральной плотности
, а график спектральной плотности 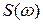 в соответствии с (8.27) представляет собой дельта функцию.
в соответствии с (8.27) представляет собой дельта функцию.
5. При 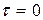 и центрированной случайной функции, получаем соотношение:
и центрированной случайной функции, получаем соотношение:
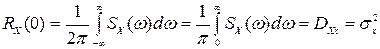 , (8.41)
, (8.41)
которое позволяет находить среднеквадратическое значение случайной функции 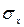 по известной спектральной плотности или корреляционной функции. Из этого выражения следует, что дисперсия стационарной функции D
по известной спектральной плотности или корреляционной функции. Из этого выражения следует, что дисперсия стационарной функции D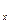 пропорциональна площади, ограниченной кривой спектральной плотности
пропорциональна площади, ограниченной кривой спектральной плотности 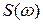 и осью абсцисс.
и осью абсцисс.
8.6. Статистические характеристики случайных
типовых процессов
Лекция 25
План лекции:
1.Статистические характеристики «белого шума».
2. Корреляционная функция и спектральная плотность скорости
изменения азимута маневрирующей цели.
3. Спектральная плотность задающего воздействия системы наведения ракеты на цель.
4. Рекомендуемая литература [9].
Рассмотрим некоторые случайные стационарные процессы, встречающиеся при исследовании САУ.
8.6.1. Белый шум
Случайный процесс, характеризуемый спектральной плотностью 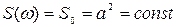 во всем диапазоне частот, т. е. имеющий равномерный на всех частотах спектр, называют белым шумом. В соответствии с (8.29) корреляционная функция белого шума имеет вид
во всем диапазоне частот, т. е. имеющий равномерный на всех частотах спектр, называют белым шумом. В соответствии с (8.29) корреляционная функция белого шума имеет вид 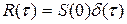 , т. е. является
, т. е. является 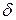 -функцией, что указывает на отсутствие корреляционной связи между любыми сколь угодно близкими друг к другу значениями случайного процесса. Процесс такого типа является математической идеализацией реального процесса.
-функцией, что указывает на отсутствие корреляционной связи между любыми сколь угодно близкими друг к другу значениями случайного процесса. Процесс такого типа является математической идеализацией реального процесса.
Дисперсия этого процесса будет бесконечно большой 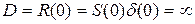 , а значит и мощность, необходимая для создания такого процесса, также бесконечна. Однако в тех случаях, когда спектр случайного воздействия значительно превосходит полосу пропускания частот исследуемой системы и равномерен в пределах этой полосы, реальный спектр можно заменить белым шумом. Случаи, когда реальный спектр помехи можно аппроксимировать белым шумом, встречаются в практике достаточно часто. Примером процесса типа белого шума является тепловой шум сопротивления.
, а значит и мощность, необходимая для создания такого процесса, также бесконечна. Однако в тех случаях, когда спектр случайного воздействия значительно превосходит полосу пропускания частот исследуемой системы и равномерен в пределах этой полосы, реальный спектр можно заменить белым шумом. Случаи, когда реальный спектр помехи можно аппроксимировать белым шумом, встречаются в практике достаточно часто. Примером процесса типа белого шума является тепловой шум сопротивления.
8.6.2. Корреляционная функция и спектральная плотность скорости изменения азимута
маневрирующей цели
Рассмотрим корреляционную функцию и спектральную плотность случайного процесса, имеющего место на входе системы автоматического сопровождения цели. Подобный сигнал представлен на рис. 8.6, а. Он характеризует изменение углового перемещения самолета — угловой координаты цели 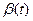 относительно системы сопровождения радиолокатора. На рис. 8.6, а видно, что кривая
относительно системы сопровождения радиолокатора. На рис. 8.6, а видно, что кривая 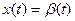 не является стационарным случайным процессом. Однако поведение цели можно представить так, будто угловая скорость движения цели в течение некоторого интервала времени остается постоянной, затем скачком меняется и на следующем интервале также остается постоянной (рис. 8.6, б).
не является стационарным случайным процессом. Однако поведение цели можно представить так, будто угловая скорость движения цели в течение некоторого интервала времени остается постоянной, затем скачком меняется и на следующем интервале также остается постоянной (рис. 8.6, б).
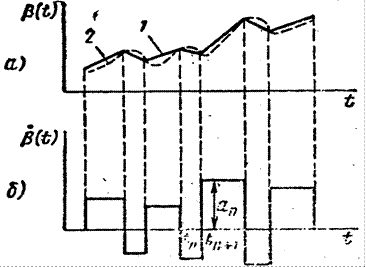
Рис. 8.6. Изменения угловой координаты маневрирующей цели (а)
и ее производной (б)
При этом моменты скачков и значения скоростей — случайные величины. Такая картина соответствует движению цели в направлении на радиолокатор и идеализированному маневру ее в горизонтальной плоскости (мгновенное изменение курса).
Значения функции 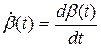 в любых двух интервалах взаимно независимы, но имеют одинаковые функции распределения вероятности.
в любых двух интервалах взаимно независимы, но имеют одинаковые функции распределения вероятности.
Случайный стационарный процесс в данном случае может быть определен так:
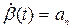 при
при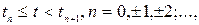 (8.42)
(8.42)
где аn— независимые случайные переменные, имеющие одинаковое распределение вероятности.
Для определения корреляционной функции необходимо найти среднее значение произведения:
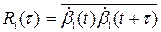 . (8.43)
. (8.43)
Возможны два случая.
Если моменты времени 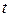 и
и 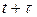 таковы, что величины
таковы, что величины 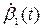 и
и 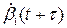 находятся в одном интервале
находятся в одном интервале 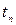 , то среднее значение произведения угловых скоростей равно среднему квадрату угловой скорости или дисперсии:
, то среднее значение произведения угловых скоростей равно среднему квадрату угловой скорости или дисперсии:
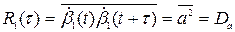 . (8.44)
. (8.44)
Если 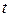 и
и 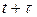 таковы, что эти величины лежат в разных интервалах, то искомое произведение скоростей равно нулю:
таковы, что эти величины лежат в разных интервалах, то искомое произведение скоростей равно нулю:
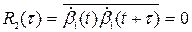 , (8.45)
, (8.45)
так как произведения с положительными и отрицательными знаками равновероятны. В результате корреляционная функция
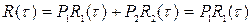 , (8.46)
, (8.46)
где P1 - вероятность нахождения значений скорости 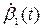 и
и 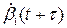 в одном интервале;
в одном интервале;
P2 = 1 - P1 — вероятность нахождения их в разных интервалах.
Обозначим через 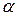 среднее число перемен скорости за 1 с. Тогда
среднее число перемен скорости за 1 с. Тогда 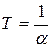 будет средним значением интервала времени, в течение которого угловая скорость сохраняет постоянную величину. Будем полагать, что вероятность появления перемены скорости в течение малого промежутка времени
будет средним значением интервала времени, в течение которого угловая скорость сохраняет постоянную величину. Будем полагать, что вероятность появления перемены скорости в течение малого промежутка времени 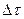 пропорциональна этому промежутку и равна
пропорциональна этому промежутку и равна 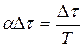 . Вероятность отсутствия перемены скорости для этого же промежутка
. Вероятность отсутствия перемены скорости для этого же промежутка 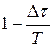 . Для интервала времени
. Для интервала времени 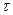 вероятность отсутствия перемены скорости, т. е. вероятность нахождения моментов времени
вероятность отсутствия перемены скорости, т. е. вероятность нахождения моментов времени 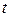 и
и 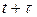 в одном интервале постоянной скорости, равна произведению вероятностей отсутствий перемены скорости в каждом элементарном промежутке
в одном интервале постоянной скорости, равна произведению вероятностей отсутствий перемены скорости в каждом элементарном промежутке 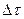 , так как эти события независимы.
, так как эти события независимы.
Следовательно, для конечного промежутка 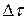
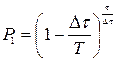 , (8.47)
, (8.47)
где 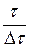 - среднее количество промежутков
- среднее количество промежутков 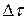 .
.
Переходя к пределу при 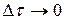 , получим
, получим
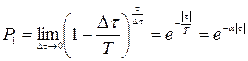 . (8.48)
. (8.48)
Функцию распределения (8.48) называют распределением Пуассона. Таким образом, искомая корреляционная функция
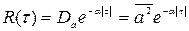 , (1.49)
, (1.49)
т. е. оказывается экспоненциально затухающей.
Спектральная плотность для рассматриваемого процесса
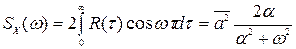 , (8.50)
, (8.50)
где 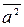 — средний квадрат угловой скорости;
— средний квадрат угловой скорости;
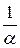 —средняя длина промежутков времени, в течение которых скорость остается постоянной. Величину
—средняя длина промежутков времени, в течение которых скорость остается постоянной. Величину 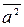 находят экспериментально на основании изучения распределения угловых скоростей слежения за самолетом, а
находят экспериментально на основании изучения распределения угловых скоростей слежения за самолетом, а 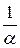 - путем определения средней продолжительности прямолинейного движения маневрирующего самолета.
- путем определения средней продолжительности прямолинейного движения маневрирующего самолета.
8.6.3. Спектральная плотность задающего воздействия системы наведения ракеты на цель
Процесс наведения ракеты на цель при телеуправлении и самонаведении может рассматриваться как процесс слежения ракеты за целью. Задающим воздействием системы при этом является закон изменения во времени угла x(t) между некоторой пространственной осью и направлением на цель (рис. 8.7).
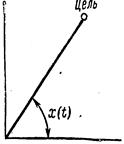
Рис. 8.7. К определению задающего воздействия
Величина x(t) оказывается случайной функцией времени ввиду случайности скорости цели, ее высоты, ракурса, маневра и т. д. Она ограничена временем, соответствующим продолжительности одной атаки.
Для того чтобы определить спектральную плотность задающего воздействия, следует рассмотреть все множество функций x(t). Такое множество функций можно представишь одной случайной функцией с неограниченным временем t (кривая 2 рис.8.6, а).
Спектральную плотность случайного процесса x(t) можно определить, заменив кривую 2 ломаной 1..
Наилучшее приближение будет тогда, когда разность между истинным значением x(t) и сглаженным изменяется по показательному закону.
Ранее была получена формула спектральной плотности (8.50) для скорости изменения входного сигнала системы автосопровождения цели.
Чтобы найти спектральную плотность задающего воздействия системы наведения ракеты на цель, необходимо перейти от производной 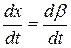 к сигналу x(t), пользуясь операторным соотношением
к сигналу x(t), пользуясь операторным соотношением 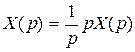 . Тогда
. Тогда
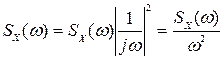 .
.
Окончательно выражение для спектральной плотности задающего воздействия x(t) принимает следующий вид:
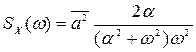 ,
,
где 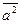 - средний квадрат угловой скорости линии визирования цели при всех возможных атаках ее ракетой;
- средний квадрат угловой скорости линии визирования цели при всех возможных атаках ее ракетой;
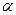 - величина, обратная среднему значению промежутков времени, в течение которых скорость линии визирования постоянна.
- величина, обратная среднему значению промежутков времени, в течение которых скорость линии визирования постоянна.
Если ломаная кривая проведена так, чтобы разность между истинным значением x(t) и сглаженным изменялась по показательному закону, то спектральная плотность случайной функции x(t) будет иметь вид:
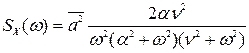 , (8.51)
, (8.51)
где 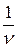 - постоянная времени показательной кривой, по которой происходит переход истинного значения случайной функции x(t) относительно сглаженной кривой.
- постоянная времени показательной кривой, по которой происходит переход истинного значения случайной функции x(t) относительно сглаженной кривой.
Таким образом, задающее воздействие наземных радиолокационных станций сопровождения и следящих головок самонаведения имеет спектральную плотность типа (8.51).
8.7. Экспериментальное определение корреляционных функций, спектральных плотностей и дисперсий
случайных процессов
Лекция 26
План лекции:
1. Экспериментальное определение корреляционной функции.
2. Экспериментальное определение спектральных плотностей.
3. Измерение дисперсии и случайного процесса.
4. Рекомендуемая литература [9].
Для определения корреляционной функции 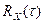 по экспериментальной реализации случайного процесса можно воспользоваться приближенной формулой
по экспериментальной реализации случайного процесса можно воспользоваться приближенной формулой
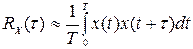 . (8.52)
. (8.52)
Точность приближения зависит от интервала наблюдения Т. Заменив интеграл (8.52) суммой, можно вычислить 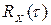 . Для вычисления корреляционной функции осциллограмму случайного процесса представляют в виде отрезков ординат, отстоящих друг от друга на расстоянии
. Для вычисления корреляционной функции осциллограмму случайного процесса представляют в виде отрезков ординат, отстоящих друг от друга на расстоянии 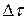 (рис. 8.8).
(рис. 8.8).
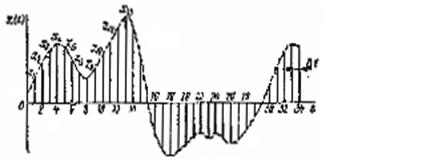
Рис. 8.8. К определению корреляционной функции
Тогда отдельные точки корреляционной функции как среднее значение попарных произведений ординат кривой реализации, отстоящих на интервал 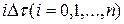 , могут быть подсчитаны с помощью выражений:
, могут быть подсчитаны с помощью выражений:
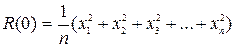 ;
;
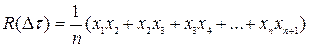 ;
;
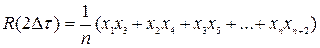 ;
;
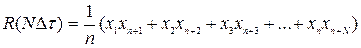 .
.
Измерение корреляционной функции производят с помощью алгоритма (рис. 8.9), в котором используется принцип перемножения значений случайного процесса, разделенных интервалом времени 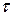 .
.
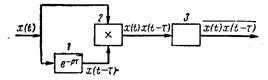
Рис. 8.9. Блок-схема вычисления корреляционной функции
Помимо перемножающего устройства 2 (рис. 8.9), вычислитель содержит элемент 1 с регулируемой задержкой 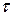 , сглаживающее устройство 3 и регистрирующее устройство. Выходная величина с множительного устройства как произведение x(t) и
, сглаживающее устройство 3 и регистрирующее устройство. Выходная величина с множительного устройства как произведение x(t) и 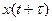 поступает на сглаживающее устройство 3, которое пропускает постоянную составляющую и медленно меняющиеся составляющие сигнала
поступает на сглаживающее устройство 3, которое пропускает постоянную составляющую и медленно меняющиеся составляющие сигнала 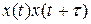 . В результате на выходе коррелятора получается приближенное значение корреляционной функции
. В результате на выходе коррелятора получается приближенное значение корреляционной функции 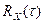 .
.
Погрешность таких корреляторов связана главным образом с ограниченным временем усреднения. Более высокую точность получают при использовании дискретных вычислительных устройств.
С помощью магнитного коррелографа график 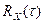 вычерчивается за 10—60 мин. Изучаемый случайный процесс в таком коррелографе записывается сразу на двух дорожках магнитной ленты с постоянным сдвигом во времени. Затем путем изменения положения одного из натяжных роликов лентопротяжного механизма на величину
вычерчивается за 10—60 мин. Изучаемый случайный процесс в таком коррелографе записывается сразу на двух дорожках магнитной ленты с постоянным сдвигом во времени. Затем путем изменения положения одного из натяжных роликов лентопротяжного механизма на величину 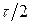 устанавливается сдвиг
устанавливается сдвиг 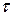 во времени между магнитными записями, считываемыми головками. Обработанный в специальном вычислительном устройстве сигнал с головок выдается на электронный потенциометр, который и производит отметку в виде точки на бумаге. Коррелограмму строят путем повторения процесса для ряда значений
во времени между магнитными записями, считываемыми головками. Обработанный в специальном вычислительном устройстве сигнал с головок выдается на электронный потенциометр, который и производит отметку в виде точки на бумаге. Коррелограмму строят путем повторения процесса для ряда значений 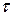 .
.
Полученные в результате экспериментальных записей корреляционные функции обычно аппроксимируют какими-либо математическими зависимостями, например типа
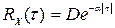 ,
,
где 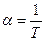 - параметр, характеризующий скорость спадания кривой.
- параметр, характеризующий скорость спадания кривой.
На практике часто встречаются и с экспоненциально-косинусной функцией
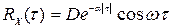 .
.
Подобный вид имеют случайные процессы типа турбулентности атмосферы, фединга радиолокационного сигнала, углового мерцания цели.
Можно показать, что любая корреляционная функция может быть аппроксимирована с желаемой степенью точности рядом, членами которого являются показательные функции
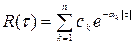 .
.
Спектральная плотность, соответствующая этой функции, определяется по формуле
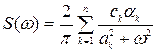 .
.
Экспериментальное определение спектральной плотности как средней величины квадрата амплитуды гармоник возможно с помощью спектрометров. Для этой цели можно использовать схему, приведенную на рис. 8.10. Исследуемая случайная функция подается на гармонический анализатор 1, который является узкополосным резонансным фильтром, настраиваемым на определенную частоту 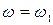 . По истечении некоторого времени на выходе фильтра выделится гармоника частотой
. По истечении некоторого времени на выходе фильтра выделится гармоника частотой 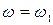 . Выходная величина фильтра 1 возводится в квадрат с помощью, например, квадратического детектора 2 и подается на инерционный измерительный прибор 3. Показания такого прибора равны среднему значению выходной величины, т. e. дают приближённые значения спектральной плотности при
. Выходная величина фильтра 1 возводится в квадрат с помощью, например, квадратического детектора 2 и подается на инерционный измерительный прибор 3. Показания такого прибора равны среднему значению выходной величины, т. e. дают приближённые значения спектральной плотности при 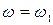 :
:
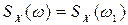 .
.
Меняя настройку анализатора, определяем ряд точек и по ним строим искомую кривую.
График 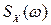 также можно получить разложением осциллограмм случайного процесса в ряд Фурье в достаточно большом интервале времени Т, принимая
также можно получить разложением осциллограмм случайного процесса в ряд Фурье в достаточно большом интервале времени Т, принимая
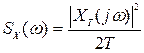 .
.
Однако чаще всего 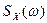 получают с помощью обработки осциллограмм случайного процесса по формуле 8.27.
получают с помощью обработки осциллограмм случайного процесса по формуле 8.27.
Спектральную плотность обычно удобно аппроксимировать дробно-рациональной функцией 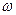 , если она получена в виде экспериментально снятой кривой.
, если она получена в виде экспериментально снятой кривой.

Рис. 8.10. Блок-схема вычисления спектральной плотности
Способы аппроксимации экспериментальных кривых такими функциями разработаны В. В. Солодовниковым.
Измерение дисперсий случайного процесса осуществляют с помощью различных дисперсиометров. Дисперсию нормального случайного процесса можно найти путем определения его среднего значения на выходе детектора, на вход которого поступает подлежащий измерению случайный процесс. На рис. 8.11 показана статическая характеристика детектора 1, случайный сигнал 2 на входе детектора и сигнал 3 на его выходе.
В соответствии с (8.9) среднее значение модуля сигнала на выходе детектора
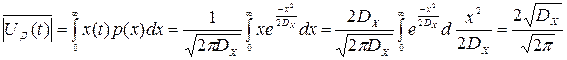 ,
,
откуда дисперсия
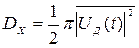 .
.
При расчете принято UВХ(t)=x(t).

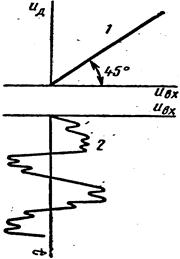
Рис. 8.11. Статическая характеристика (7) и сигналы на входе (2)
и выходе (3) детектора
В качестве усредняющего устройства в схеме дисперсиометра используется интегратор со сбросом, осуществляемым автоматически.
Напряжение на выходе интегратора за время усреднения определяется количеством сбросов (с максимальным напряжением) и остаточным напряжением, которое измеряется прибором. Среднее значение модуля случайного сигнала 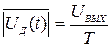 ,
,
где UВЫХ — напряжение на выходе интегратора за время усреднения; Т — время усреднения.
8.8. ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ
ЧЕРЕЗ ЛИНЕЙНУЮ систему
Лекция 27
План лекции:
1. Интегральное уравнение связи между процессами
на выходе и входе линейных систем.
2. Рекомендуемая литература [9].
8.8.1. Интегральное Уравнение связи
между характеристиками процессов
на выходе и входе линейных систем
Спектральная пл
 2014-02-02
2014-02-02 4008
4008