Модуль 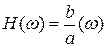 АФЧХ
АФЧХ 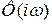 называется амплитудной частотной характеристикой (АЧХ).
называется амплитудной частотной характеристикой (АЧХ).
АЧХ представляет собой зависимость отношения амплитуды входного и выходного сигналов от частоты внешнего воздействия. Она показывает степень искажения системой или звеном входного сигнала по амплитуде на различных частотах.
Аргумент 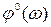 АФЧХ
АФЧХ 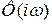 называется фазовой частотной характеристикой (ФЧХ). ФЧХ представляет собой зависимость сдвига фаз входного и выходного сигналов от частоты входного воздействия. Она показывает степень искажения системой или звеном входного сигнала по фазе на различных частотах. АФЧХ строится на комплексной плоскости в координатах,
называется фазовой частотной характеристикой (ФЧХ). ФЧХ представляет собой зависимость сдвига фаз входного и выходного сигналов от частоты входного воздействия. Она показывает степень искажения системой или звеном входного сигнала по фазе на различных частотах. АФЧХ строится на комплексной плоскости в координатах,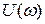 и
и 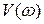 . Она представляет собой геометрическое место концов вектора
. Она представляет собой геометрическое место концов вектора 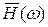 (годограф), соответствующее частотной передаточной функции при изменении частоты
(годограф), соответствующее частотной передаточной функции при изменении частоты 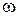 от нуля до бесконечности (рис. 3.1,а)
от нуля до бесконечности (рис. 3.1,а)
АФЧХ может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции 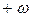 на
на 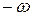 получается сопряжённая комплексная величина. Поэтому АФЧХ для отрицательных частот может быть построена как зеркальное изображение относительно вещественной оси АФЧХ для положительных частот.
получается сопряжённая комплексная величина. Поэтому АФЧХ для отрицательных частот может быть построена как зеркальное изображение относительно вещественной оси АФЧХ для положительных частот.
Из рис. 3.1, а следует зависимости, связывающие модуль 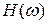 и аргумент
и аргумент 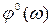 АФЧХ с действительной
АФЧХ с действительной 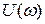 и мнимой
и мнимой 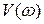 частями частотной передаточной функции:
частями частотной передаточной функции:
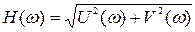 ; (3.24)
; (3.24)
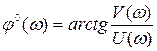 ;
;
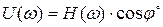 ;
;
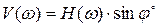 . (3.25)
. (3.25)
Формулы (3.24) и (3.25) позволяют аналитически определить АЧХ и ФЧХ по передаточной функции системы или звена.
На рис. 3.1. б показаны примеры амплитудной и фазовой частотных характеристик обычных инерционных звеньев. У таких звеньев в силу их инерционности АЧХ по мере увеличения частоты приближается к оси частот.
При этом, чем менее инерционно звено, тем длиннее его амплитудная характеристика, т.е. тем больше полоса пропускания. Теоретически АЧХ продолжается до бесконечности, но практически полоса пропускания оценивается значением частоты, при котором отношение амплитуд 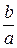 становится меньше определенного достаточно малого конечного значения. Это значение обычно берут равным 5%.
становится меньше определенного достаточно малого конечного значения. Это значение обычно берут равным 5%.
Наличие максимума у АЧХ говорит о резонансных свойствах звена или системы. Частота, соответствующая максимуму АЧХ, называется резонансной частотой.
Для получения частотных характеристик экспериментальным путём для каждого значения частоты определяют амплитуду гармонического входного воздействия, амплитуду выходной величины, а также фазовый сдвиг между обеими амплитудами.
Ценность использования частотных характеристик заключается в том, что они позволяют косвенно, т.е. без решения дифференциального уравнения системы, судить о поведении САУ в отношении устойчивости и ряда показателей качества, а также определять и рассчитывать средства коррекции системы для получения заданных динамических показателей.
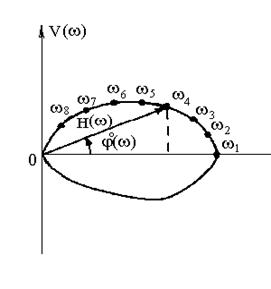
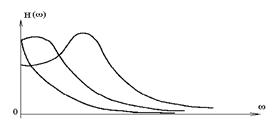
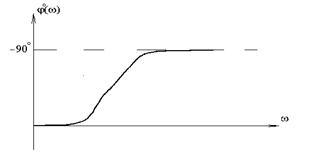
Рис. 3.1
ЛОГАРИФМИЧЕСКИЕ АМПЛИТУДННЫЕ И ФАЗОВЫЕ
В настоящее время наибольшее применение получили логарифмические частотные характеристики. Их применяют как для анализа, так и для синтеза линейных и нелинейных систем автоматического управления.
Такое признание логарифмические характеристики получили благодаря своим достоинствам, которые, прежде всего, сводятся к простоте их построения и наглядности получаемых результатов.
Построение ЛАФЧХ производится фактически без расчётов по известным логарифмическим характеристикам типовых звеньев с применением шаблонов этих характеристик. Структурная схема САУ должна быть сведена при этом к схеме, состоящей из последовательно соединённых типовых звеньев с единичными местными обратными связями. К указанному виду можно свести любую схему на основании правил преобразования структурных схем.
Эквивалентная передаточная функция 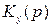 последовательно соединенных звеньев равна произведению передаточных функций этих звеньев, т.е.
последовательно соединенных звеньев равна произведению передаточных функций этих звеньев, т.е.
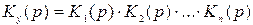 .
.
Следовательно
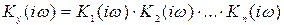 ,
,
или
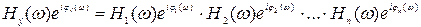 . (3.26)
. (3.26)
На основании (3.26) будем иметь:
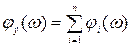 ; (3.27)
; (3.27)
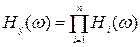 . (3.28)
. (3.28)
В результате логарифмирования выражения (3.28) получим
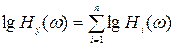 , (3.29)
, (3.29)
т.е. в логарифмическом масштабе амплитудная частотная характеристика последовательно соединенных звеньев равна сумме амплитудных характеристик отдельных звеньев. Это позволяет строить логарифмические амплитудные и фазовые частотные характеристики (ЛАФЧХ) разомкнутых систем путем геометрического сложения соответствующих характеристик типовых звеньев, на которые разбивается система. Это существенно сокращает время построения частотных характеристик сложных САУ.
Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (ЛАХ) и логарифмическую фазовую частотную характеристику (ЛФХ). Для построения ЛАХ находится величина
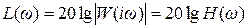 . (3.30)
. (3.30)
Эта величина выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела - в 100 раз, 3 бела - в 1000 раз и т.д.
Децибел равен одной десятой части бела. Если бы 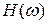 было отношением мощностей, то перед логарифмом в правой части (3.30) должен был бы стоять множитель 10. Так как
было отношением мощностей, то перед логарифмом в правой части (3.30) должен был бы стоять множитель 10. Так как 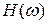 представляет собой отношение не мощностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов и т.п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в сто раз, что соответствует двум белам или двадцати децибелам. Поэтому в правой части (3.30) стоит множитель 20.
представляет собой отношение не мощностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов и т.п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в сто раз, что соответствует двум белам или двадцати децибелам. Поэтому в правой части (3.30) стоит множитель 20.
Для построения ЛАЧХ и ЛФЧХ используется стандартная сетка (рис. 3.2). По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие 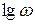 , и пишется само значение частоты w в рад/сек. Для этой цели можно использовать специальную полулогарифмическую бумагу. За единицу приращения
, и пишется само значение частоты w в рад/сек. Для этой цели можно использовать специальную полулогарифмическую бумагу. За единицу приращения 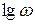 принимают декаду, соответствующую десятикратному изменению частоты. Применяется также деление оси абсцисс на октавы. Октава соответствует изменению частоты в два раза.
принимают декаду, соответствующую десятикратному изменению частоты. Применяется также деление оси абсцисс на октавы. Октава соответствует изменению частоты в два раза.
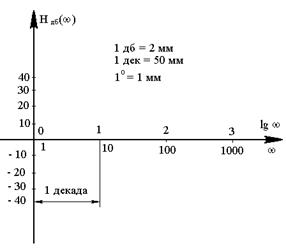
Рис 3.2
По оси ординат откладывается модуль в децибелах (дБ). Для этой цели на ней наносится равномерный масштаб. Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля 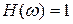 (т.е.
(т.е. 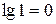 ). Ось ординат может пересекать ось абсцисс (ось частот) в произвольном месте. Следует учесть, что точка
). Ось ординат может пересекать ось абсцисс (ось частот) в произвольном месте. Следует учесть, что точка 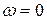 лежит на оси частот слева в бесконечности, т.к.
лежит на оси частот слева в бесконечности, т.к. 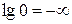 . Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход ЛАЧХ.
. Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход ЛАЧХ.
Для построения ЛФЧХ используется та же ось абсцисс (ось частот). По оси ординат откладывается фаза в градусах в линейном масштабе. Построение ЛАФЧХ ведется с помощью шаблонов, поэтому целесообразно придерживаться следующих масштабов: 1 дБ = 2 мм; 1° = 1 мм; 1 дек. = 50 мм.
Лекция 8
План лекции:
1. ЛАФЧХ типовых звеньев.
2. Особенности частотных характеристик устойчивых и минимально-
фазовых звеньев.
3. Рекомендуемая литература [1, 3, 8].
3.5. Частотные характеристики типовых звеньев
Выше было отмечено, что ЛАФЧХ любой, как угодно сложной САУ, можно построить практически без расчетов по известным ЛАФЧХ типовых звеньев, которые сведены в табл. 3.1.
1. Усилительное звено. Передаточная функция этого звена 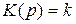 . Амплитудно-фазовая частотная характеристика имеет вид
. Амплитудно-фазовая частотная характеристика имеет вид
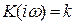 . (3.31)
. (3.31)
Согласно (3.24), (3.25) и (3.31) имеем:
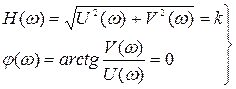 . (3.32)
. (3.32)
Логарифмическая амплитудная частотная характеристика
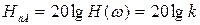 . (3.33)
. (3.33)
Анализ (3.32) и (3.33) показывает, что ЛАХ усилительного звена не зависит от частоты, а ФЧХ равна 0.
2. Интегрирующее звено. Передаточная функция этого звена имеет вид 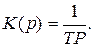 АФЧХ равна
АФЧХ равна 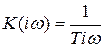 . (3.34)
. (3.34)
Согласно (3.34) имеем:
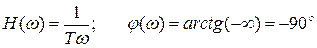 . (3.35)
. (3.35)
На основании (3.35)
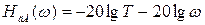 . (3.36)
. (3.36)
ЛАХ пересекает ось частот при 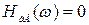 т.е.
т.е.
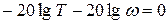 , или
, или 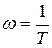 . (3.37)
. (3.37)
Найдем изменение ЛАХ (по амплитуде) при изменении частоты на одну декаду
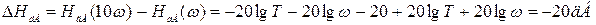 .(3.38)
.(3.38)
Таким образом, ЛАХ интегрирующего звена согласно (3.36), (3.37) и (3.38) представляет собой прямую линию с наклоном (-20) дБ/дек, пересекающую ось частот при 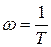 .
.
3. Апериодическое (инерционное) звено. Передаточная функция этого звена имеет вид
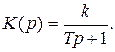
АФЧХ равна
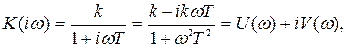 (3.39)
(3.39)
где
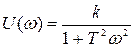 ;
; 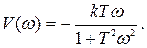
Согласно (3.39) АЧХ и ФЧХ имеют вид:
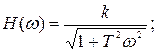
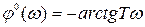 . (3.40)
. (3.40)
ЛАЧХ апериодического звена
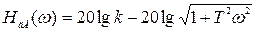 (3.41)
(3.41)
может быть приближенно представлена ломаной линией. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика построена из двух асимптот, к которым стремится ЛАЧХ при w ® 0 и w ® ¥. Найдем эти асимптоты.
При малых значениях w<< 1/T в выражении (3.41)
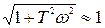 т.е.
т.е. 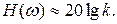
В этом случае характеристика представляет собой прямую, параллельную оси частот и проходящую на уровне 20lg k. Это есть низкочастотная асимптота, к которой стремится ЛАЧХ при w ® 0.
С другой стороны, на больших частотах, когда w >> 1/T имеем
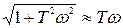 , т. е.
, т. е. 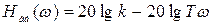 .
.
В этом случае характеристика представляет собой прямую, имеющую наклон (-20) дБ/дек. Действительно, при увеличении w на 1 декаду, т.е. в 10 раз
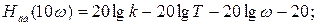
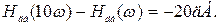
Эта линия является высокочастотной асимптотой, к которой стремится ЛАЧХ при w ® ¥. Обе асимптоты пересекаются на сопрягающей частоте w = 1 /T.
При w =1/ T согласно (3.41) имеем
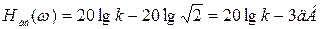 .
.
Таким образом, максимальное расхождение между истинной и асимптотической ЛАЧХ равно всего 3 дБ. Поэтому при практических построениях используют обычно асимптотическую ЛАЧХ.
Фазовая частотная характеристика, соответствующая выражению (3.40), при w®¥ изменяется от 0 до (–p/2). При этом в точке w = 1 /T фазовая характеристика j (w) = - p / 4.
Если частотные характеристики получены экспериментально, по ним нетрудно определить параметры звена Т и k, пользуясь описанной выше зависимостью между этими характеристиками и передаточной функцией.
4. Колебательное звено. Передаточная функция колебательного звена имеет вид
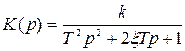 . (3.42)
. (3.42)
АФЧХ 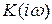 , согласно (3.42), равна
, согласно (3.42), равна
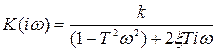 . (3.43)
. (3.43)
Исходя из выражения (3.43) получим:
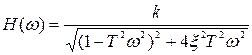 ; (3.44)
; (3.44)
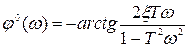 . (3.45)
. (3.45)
На основании (3.44) можно записать
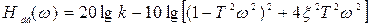 . (3.46)
. (3.46)
Тогда ЛАЧХ можно представить в виде двух асимптот, к которым она стремится при w ® 0 и w ® ¥.
Уравнение низкочастотной асимптоты получается из (3.46) при w<< 1/T
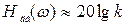 .
.
Уравнение высокочастотной асимптоты при x = 0имеет вид
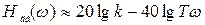 . (3.47)
. (3.47)
Из последнего выражения следует, что при увеличении частоты w на 1 декаду ЛАЧХ понижается на 40 дБ, что и определяет наклон высокочастотной асимптоты в (- 40) дБ/дек. В области средних частот (w» 1 /T) асимптотическую ЛАЧХ корректируют с помощью готовых графиков поправок, дающих разность между истинной к асимптотической ЛАЧХ. Графики поправок (рис.3.3.) и фазовые частотные характеристики колебательного звена (рис.3.3.) существенно зависят от величины x.
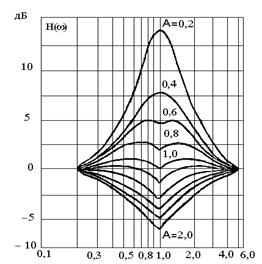
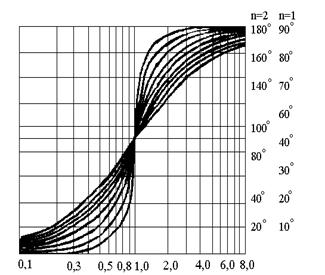
Рис.3.3
Таблица 3.1
| № п/п | Типовое звено | Передаточная функция | ЛАФЧХ |
| Усилительное | k | 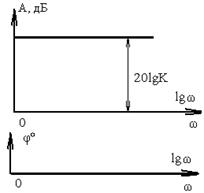 | |
| Дифференцирующее | Tp | 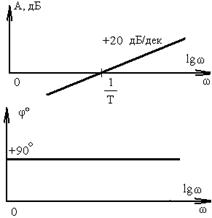 | |
| Интегрирующее | 1 / Tp | 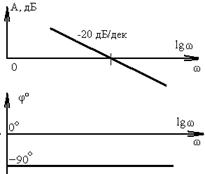 | |
| Апериодическое | 1 / (Tp+1) | 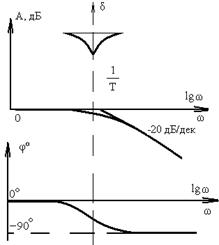 | |
| Форсирующее первого порядка | Tp+1 | 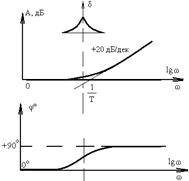 | |
| Форсирующее второго порядка | 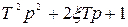 | 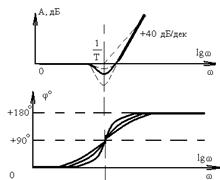 | |
| Колебательное | 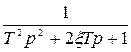 | 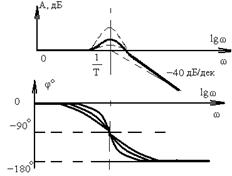 | |
Колебательное при 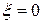 (демпфирование отсутствует) (демпфирование отсутствует) | 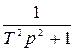 | 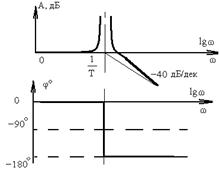 | |
Форсирующее звено второго порядка при 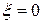 | 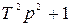 | 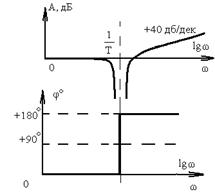 | |
| Неустойчивое форсирующее звено первого порядка | Tp-1 | 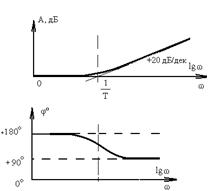 | |
| Неустойчивое форсирующее звено второго порядка | 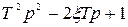 | 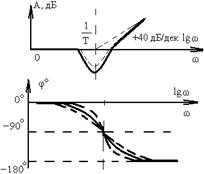 | |
| Неустойчивое апериодическое | 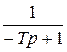 |  | |
| Фазоинверсное | - 1 |  | |
| Неустойчивое колебательное | 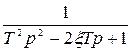 |  |
5. Дифференцирующее и форсирующее звенья. ЛАФЧХ дифференцирующего и форсирующих (первого и второго порядка) звеньев можно получить зеркальным отражением относительно оси частот соответственно интегрирующего, апериодического и колебательного звеньев.
3.6. Особенности частотных характеристик устойчивых
и минимально-фазовых звеньев
В общем случае исчерпывающее описание звена с помощью частотных характеристик требует знания АФЧХ W(iw), либо любой пары функций: H(w) и j(w) или U(w) и V(w).
Однако оказывается, что для некоторого класса звеньев существует однозначная связь между образующими эти пары функциями, и поэтому для полного описания таких звеньев достаточно иметь только одну из них.
Остановимся вначале на связи между действительной U(w) и мнимой V(w) частотными функциями. Доказано, что в случае устойчивых звеньев эти функции однозначно связаны, т.е. по любой из них можно найти другую. Устойчивым звеном называется звено, все полюсы передаточной функции которого имеют отрицательные действительные части.
Теперь обратимся к определению связи между амплитудной H (w) и фазовой j (w) частотными функциями. Доказано, что эти функции однозначно связаны у минимально-фазовых звеньев. Минимально-фазовым звеном называется звено, у которого все полюсы и нули передаточной функции имеют отрицательные или равные нулю действительные части. Свое название минимально-фазовые звенья получили в связи с тем, что они дают минимальный фазовый сдвиг j по сравнению с любыми звеньями, имеющими такую же амплитудную функцию H (w), но у которых указанное выше условие в отношении полюсов и нулей передаточной функции не выполняется. Чтобы проиллюстрировать последнее, рассмотрим звено с уже знакомой нам передаточной функцией
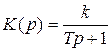 .
.
Согласно определению, это звено является минимально-фазовым, так как, его единственный полюс равен -1/Т, т.е. отрицательный действительный, а нулей вообще нет. Амплитудно-фазовая функция этого звена
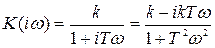
и, следовательно, амплитудная функция равна
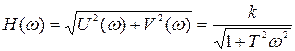 ,
,
а фазовая
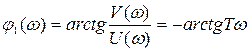 .
.
При w ® ¥ значение j изменяется от 0 до (–p/2).
Рассмотрим теперь звено с передаточной функцией
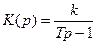 .
.
Это звено не является минимально-фазовым, так как его передаточная функция имеет положительный действительный полюс (+ 1 /Т). Заметим, что по этой причине данное звено является также и неустойчивым. Амплитудно-фазовая функция этого звена имеет вид
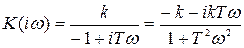 .
.
Его АЧХ совпадает c АЧХ первого звена, а фазовая функция равна
j (w) = arctgTw – p.
При w ® ¥ значение j изменяется от (- p)до (– p / 2). Таким образом, второе звено создает большее фазовое запаздывание, чем первое, являющееся минимально-фазовым.
Для графического описания минимально-фазовых звеньев применяют только АЧХ. В случае необходимости по ней может быть построена ФЧХ. Принципиально связь между этими характеристиками такова, что величина фазы j растет с увеличением наклона АЧХ. При этом в случае применения ЛАЧХ можно приближенно считать, что участку ЛАЧХ с наклоном (- 20) дБ/дек соответствует фазовый сдвиг, близкий к (– p/2), а участку ЛАЧХ с наклоном (- 40) дБ/дек – сдвиг (- p). Конкретно взаимосвязь между ЛАЧХ и ЛФЧХ можно проследить на примере характеристик, приведенных в табл. 3.1.
4. УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Лекция 9
План лекции:
1. Понятие об устойчивости заданного режима.
2. Определение устойчивости по Ляпунову.
3. Критерий устойчивости Гурвица.
4. Рекомендуемая литература [1, 2, 7].
4.1. ОБЩИЕ ПОНЯТИЯ ОБ УСТОЙЧИВОСТИ ЗАДАННОГО РЕЖИМА
В САУ одним из основных является понятие устойчивости заданного режима. Заданным режимом может быть состояние равновесия, при котором обобщенные координаты САУ имеют заданные постоянные значения.
САУ всегда подвергается действию внешних возмущений, которые стремятся вывести ее из состояния равновесия. Если САУ устойчива, она противостоит этим внешним воздействиям, а будучи выведенной из состояния равновесия, с определенной точностью возвращается к нему.
На рис.4.1 а изображен шар, лежащий на вогнутой поверхности. При всяком отклонении его от состояния равновесия возникает сила, которая стремится вернуть шар в положение равновесия. Это положение равновесия называется устойчивым.
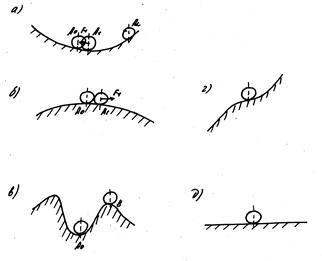
Рис. 4.1
На рис.4.1 б шар лежит на выпуклой поверхности, и любое отклонение его от положения равновесия вызовет силу, которая будет стремиться еще дальше увести его от положения равновесия. Это неустойчивое положение.
На рис. 4.1 в состояние равновесия А0 устойчиво лишь до тех пор, пока отклонения не вышли за границу, определяемую точкой В. Выйдя за эту границу, шар уже не вернется в точку А0. В этом случае мы называем точку А0 устойчивой в малом (т.е. при малых отклонениях от равновесия) и неустойчивой в большом, если при больших отклонениях.
Из возможных состояний равновесия бывают еще полуустойчивые (рис. 4.1 г) и безразличные (рис. 4.1 д) состояния равновесия.
Кроме устойчивости равновесия, существует и устойчивость движения.
Пусть на систему действуют внешние силы, в результате чего ее движение совершается по некоторой обобщенной траектории, определяемой решением уравнений движения, т.е. функциями у1(t), у2(t), …, уn(t). Можно указать то движение, которое надо сообщить системе. Назовем его заданным движением у*1(t), у*2(t), …, у*n(t).
Заданное движение называется невозмущенным движением. Но если на систему, кроме заданных, подействуют дополнительные внешние воздействия, которые затем перестанут действовать, то под их влиянием САУ перейдет в новое, возмущенное движение.
Заданное невозмущенное движение называется устойчивым, если в результате действия возмущений возмущенное движение с течением времени войдет в некоторую заданную область, определяемую величинами
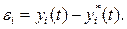
После этих предварительных замечаний перейдем к определению устойчивости, которое было дано А. М. Ляпуновым.
Примем, что рассматриваемая система описывается нелинейными дифференциальными уравнениями вида
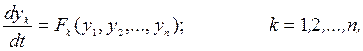 (4.1)
(4.1)
где ук – обобщенные координаты системы, Fk – нелинейная функция.
Пусть в начальный момент t = t0 начальные значения координат равны у 10 , у 20 , у 30 , …, ук 0 , а каждой совокупности начальных значений соответствует
единственное решение уравнений (4.1) для всех t > t 0 :
у к = у к (у10 , у20 , у30 , …, у n0,t). (4.2)
Установившиеся процессы описываются тривиальными решениями уравнений (4.1):
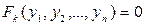 , (4.3)
, (4.3)
решая которые, найдем у*1, у*2, …, у* n.
Введем отклонения хк координат от установившихся значений ук:
х к = у к – у*n. (4.4)
Подстановка отклонений (4.4) в уравнения (4.1) приводит к системе уравнений
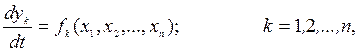 (4.5)
(4.5)
где fk – нелинейная функция.
 2014-02-02
2014-02-02 2057
2057








