Лекция 14 7 страница

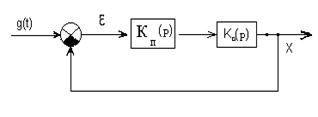
Рис. 6.9

Применительно к принятым на рисунке обозначениям можно написать:

Wc(р) = Kп(р)K0(р),

или Wc(iw)= Kп(iw)K0(iw), (6.6)

где Wc(iw) выражение для АФЧХ разомкнутой скорректированной системы. На основании (6.6) имеем

20lg ½ Wc(iw) ½ = Hc(w)_дБ = Нж.дБ(w) = Нп.дБ(w)+ Но.дБ(w), (6.7)

где Нс.дБ(w) - ЛАЧХ скорректированной системы, которая должна совпадать с желаемой ЛАЧХ. Из выражения (6.7) следует,что

Нп.дБ (w)=Нж.дБ (w) - Но.дБ (w). (6.8)

Из приведенных соотношений вытекает следующий порядок выполнения расчетов при синтезе САУ с последовательным КУ:

1. Строится ЛЧАХ исходной нескорректированной системы (располагаемая ЛАХ).

2. По заданным требованиям к качеству переходного про­цесса и к точности САУ строится ЛАЧХ скорректированной систе­мы, т.е. желаемая ЛАЧХ.

3. Учитывая, что в минимально-фазовых системах (какими являются в основном системы регулирования) имеется однознач­ная связь между амплитудными и фазовыми характеристиками, по имеющимся ЛАЧХ строят соответствующие ЛФЧХ и определяют запасы по фазе и по амплитуде.

4. Вычитанием ЛАЧХ исходной системы из ЛАЧХ скорректи­рованной системы получают ЛАЧХ, корректирующего устройства Нп.дБ(w).

5. По полученной ЛАЧХ корректирующего устройства подби­рается наиболее простое по техническому исполнению корректирующее устройство.

6. Если ЛАЧХ выбранного корректирующего устройства будет несколько отличаться от расчетной, то необходимо постро­ить окончательную ЛАЧХ скорректированной системы и по ней проверить полученные показатели переходного процесса.

6.7. СИНТЕЗ ПАРАЛЛЕЛЬНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА

Задана передаточная функция разомкнутой цепи K0(p). Тре­буется ввести корректирующую обратную связь Z(p) так, чтобы система в целом (рис. 6.10) обладала желаемой частотной ха­рактеристикой.

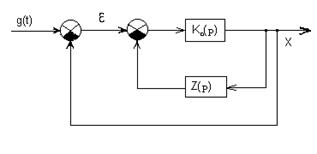
Рис. 6.10

Передаточная функция разомкнутой цепи с коррекцией равна

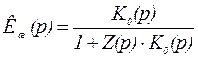. (6.9)

Следовательно

.

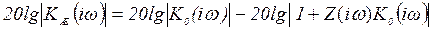Чтобы избавиться от суммы под знаком логарифма, запишем приближенное выражение

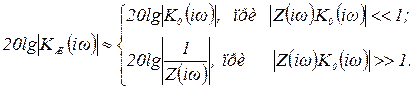(6.10)

Построим ЛАЧХ неизменной части системы с передаточной функцией К0, имеющей желаемый коэффициент усиления, а также желаемую ЛАФЧ Кж (рис. 6.11).

.

В качестве искомой характеристики 1/Z(p) примем характе­ристику, обозначенную на рис. 6.11 точечным пунктиром и совпадающую в средней части с Кж. Вычтем 1/Z из характер­истики К0. Получим

.

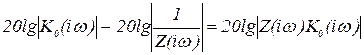Этот результат показан на рис. 6.11 штрихпунктирной линией. Из графика видно, что на участке CD характеристика½ ZK0 ½ >1, а до точки С и после точки D характеристика ½ ZK0 ½ <1 так как ось абсцисс соответствует значению амплитуды, равному 1 (20 lg А=0).

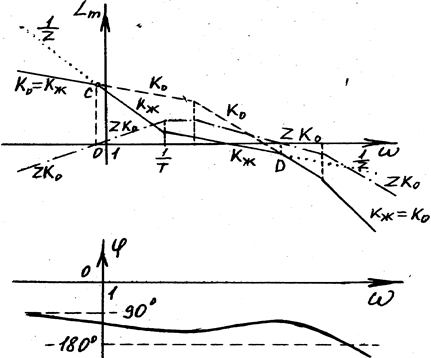
Рис.6.11

Следовательно, при принятом очертании исходной характеристики 1/Z удовлетворяются написанные выше приближенные равенства (6.10).

Таким образом, найдено параллельное корректирующее устройство в виде обратной связи, которое создает для системы в целом близкую к желаемой частотную характеристику. Согласно рис.6.11 логарифмическая характеристика 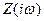получит вид, представленный на рис. 6.12, что соответствует следующей пе­редаточной функции искомой корректирующей обратной связи:

.

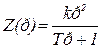Это есть гибкая инерционная обратная связь с двойным дифференцированием (т.е. обратная связь по угловому ускорению исполнительного привода следящей системы).

1/T

w

Рис. 6.12

7. МЕТОДЫ СИНТЕЗА, ОСНОВАННЫЕ НА ТЕОРИИ

ПРОСТРАНСТВА СОСТОЯНИЙ

ЛЕКЦИЯ 20

План лекции:

1. Рассказать о составлении уравнений САУ в пространстве состоя­ний.

2. Рассмотреть пример.

3. Рекомендуемая литература [4, 6].

7.1. Уравнения системы в пространстве состояний

При исследовании динамических свойств САУ классическими методами после составления дифференциальных уравнений для отдельных элементов системы обычно переходят к передаточным функциям. Да­лее составляют общую структурную схему САУ, в которой отдельные элементы представляются блоками с соот­ветствующими передаточными функциями. Затем определяют пе­редаточную функцию замкнутой системы, характеризующую связь между изображениями по Лапласу входной и выходной величины САУ.

Поведение системы во времени можно характеризо­вать не только выходной величиной САУ, но и промежуточ­ными переменными в цепи системы, число которых равно порядку системы n. Таким образом, получается n -мерный вектор состоя­ния, множество возможных положений которого образует вектор­ное пространство, называемое пространством состояний системы.

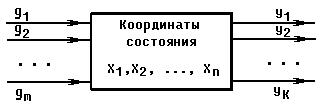
Рис. 7.1

Будем рассматривать общий случай обыкновенных линейных САУ

(рис. 7.1), описываемых системой дифферен­циальных уравнений в нормальной форме в векторно-матричной записи

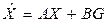; (7.1)

Y = CX,

где X - вектор состояния системы, Y - вектор выходных вели­чин, G - вектор внешних воздействии (задающих и возмущающих), т.е:

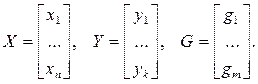
Через А, В, С обозначены:

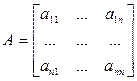- собственная параметрическая матрица САУ;

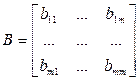- входная матрица САУ;

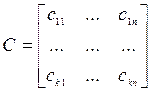- выходная матрица САУ.

Процессы в системе при свободном движении (без внешних воздействий) согласно (7.1) описываются векторно-матричным уравнением вида

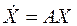, (7.2)

которое имеет следующее характеристическое уравнение:

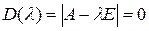. (7.3)

В развернутой форме векторное уравнение (7.2) записывается следующей системой дифференциальных уравнений:

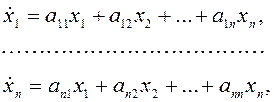(7.4)

Характеристическое уравнение (7.3) в развернутой форме имеет вид

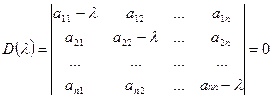. (7.5)

В качестве примера рассмотрим вывод уравнений состояния электромеханической следящей системы, принципиальная схема которой приведена на рис. 7.2.

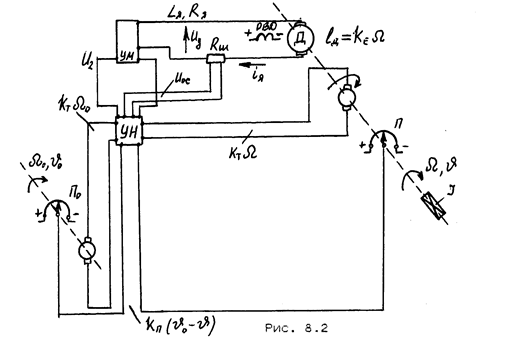
Рис. 7.2

В этой системе введены обратные связи по углу поворота, ско­рости вращения и току в цепи якоря двигателя. Обозначение переменных ясны из чертежа.

Для электродвигателя постоянного тока имеем:

1) уравнение электрической цепи

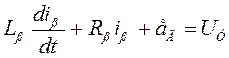; (7.6)

2) уравнение механической цепи

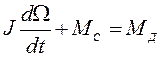, (7.7)

где М_С=γΩ - момент сопротивления; М_Д=k_М i_Я - момент двигателя; е_Д=k_E Ω – противо-э.д.с двигателя.

Через γ, k_{М ,} k_E обозначены соответствующие коэффициенты.

Преобразуя выражения (7.6) и (7.7), получим уравнения двигателя в виде

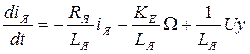; (7.8)

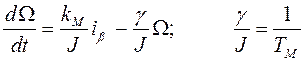. (7.9)

Для входной цепи усилителя напряжения имеем

,

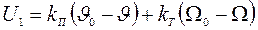где 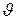_о , Ω_о – внешние входные воздействия (угол и угловая скорость поворота задающего вала);

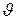, Ω – выходные величины системы (угол и угловая скорость поворота выходного вала).

Для входной цепи усилителя мощности запишем

U₂ = K₁U₁ - K_ocU_oc,

где U_oc=R_ш i_Я .

Выходное напряжение усилителя мощности УМ, с учетом предыдущего выражения, будет равно

U_у = K_умU₂=К_умК₁U₁ - K_умK_осR_шi_Я.

После подстановки получим

U_у = K_умK₁[К_П( 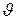_о - 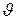)+К_Т(Ω_о-Ω)]-K_умK_осR_шi_Я. (7.10)

Совместно (7.8) и (7.10) дают уравнение

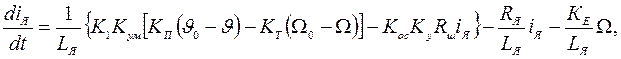которое может быть представлено в виде

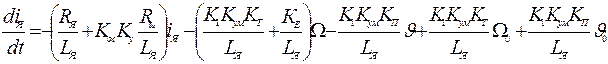.(7.11)

Скорость вращения

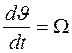. (7.12)

Систему из трех уравнений (7.11), (7.9) и (7.12) запишем в векторно-матричной форме:

.

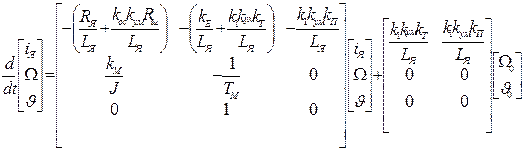Введем обозначения i_Я=x₁; Ω=x₂; 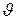=x₃ – координаты вектора состояний следящей системы. Обозначим также:

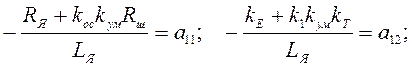
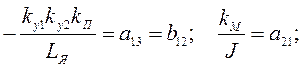
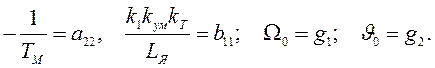
В результате получим уравнение состояний следящей системы в стандартной векторно-матричной форме

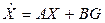, (7.13)

где X – вектор состояний системы, G – входной вектор, причем

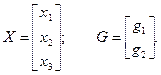
Параметрическая матрица состояния системы А и входная матрица В имеют вид:

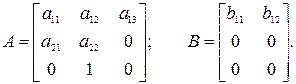
Соответствующая структурная схема cистемы представлена на рис. 7.3.

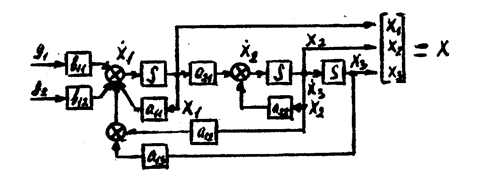
Рис. 7.3

Она составлена по уравнениям вида

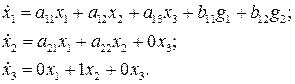
Дополним уравнение (7.13) уравнением выхода.

Y=CX.

Поскольку в наших обозначениях выходные величины Ω=x₂, 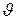=x₃, то в этом уравнении координатами выходного вектора системы

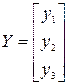
будут величины y₁=0, y₂=x₂= Ω, y₃=x₃= 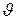, поэтому выходная мат­рица системы будет иметь вид

.

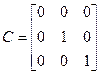Таким образом, при введении в систему корректирующих фильтров за счет дополнения основных уравнений системы уравнениями цепей коррекции, пространство состояний корректируе­мой системы расширяется. Порядок системы увеличивается, од­нако число свободно подбираемых параметров увеличивается еще больше.

В качестве примера составим уравнения состояния интегро-дифференцирующего корректирующего звена (рис. 7.4 и 7.5).

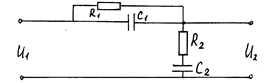
Рис. 7.4

В качестве координат состояния целесообразно выбрать напря­жения на конденсаторах, характеризующие накопление количест­ва электричества. Получим

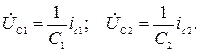
Но, так как

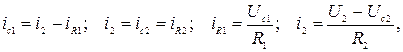
то после подстановки и простых преобразовании будем иметь следующие уравнения состояния:

.

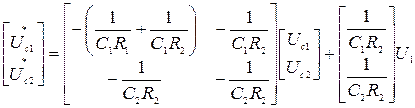Структурная схема в пространстве состояний, составленная по уравнениям данного корректирующего звена, приведена на рис. 7.5

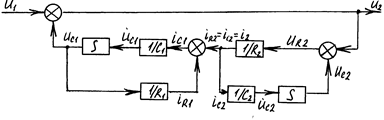
Рис. 7.5

Выходная величина U₂=U₁-U_C1.

Включение последовательно подобранного корректирующего звена расширяет пространство состояний на две координаты, однако число свободных варьируемых параметров С₁, С₂, R₁, R₂ равно четырем.

ЛЕКЦИЯ 21

План лекции:

1. Коррекция системы в пространстве состояния.

2. Корневой метод синтеза САУ по координатам пространства состоянии.

3. Прямой метод синтеза корректирующей обратной связи следя­щей

системы.

4. Рекомендуемая литература [4].

7.2. Коррекция системы в пространстве состояний

При расчете систем управления в пространстве состояний надо иметь в виду, что не все координаты состояния могут быть технически измеряемыми. Это часто является или чрезвычайно затруднительным, или технически невозможным.

Пусть А⁰ обозначает матрицу нескорректированного объекта управления. Положим, что r координат вектора x⁰ технически измеряемы, a h координат - неизмеряемы. Для кор­рекции системы так называемым методом "расширения пространс­тва состояний" введем блочную, окаймленную рядами нулей, матрицу

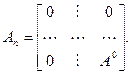(7.14)

Теперь уравнение объекта управления в векторно-матричной форме будет

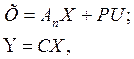
где U и Y - векторы соответственно управления и выхода, Р и С - матрицы соответствующих порядков.

Закон управления запишем в виде

,

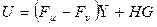где F_μ и F_ν - матрицы, которые являются функциями пара­метров последовательных корректирующих устройств (корректи­рующих фильтров) μ=­{μ₁, …, μ_n-τ} и параметров отрицательных обратных связей ν={ν₁, …, ν_γ}, H – входная матрица управления.

Для замкнутой системы получим

,

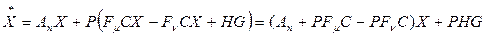или

,

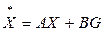где

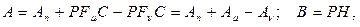
т.е. последовательная коррекция определяется матрицей A_μ=PF_μC, заполняющей нулевые места блочной матрицы (7.14), т.е.

.

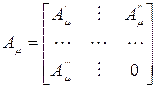Корректирующее влияние обратных связей несет в себе матрица A_ν=PF_νC, входящая в основную часть блочной матрицы (7.14), т.е.

.

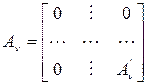Свободное движение скорректированной системы описывается векторно-матричным уравнением вида

,

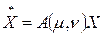которому соответствует характеристическое уравнение

.

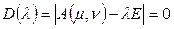В развернутом форме характеристическое уравнение имеет вид

,

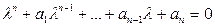где коэффициенты есть функции от параметров объекта и параметров корректирующих цепей:

.

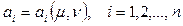7.3. Прямой корневой метод синтеза

доминантного типа

О качестве процесса управления можно судить по располо­жению корней характеристического уравнения (т.е. полюсов пе­редаточной функции замкнутой системы), учитывая также еще и операторный многочлен в правой части дифференциального урав­нения (т.е. нули передаточной функции замкнутой системы).

В настоящее время разрабатываются различные корневые методы расчета, автоматических систем. Наиболее перспективным из корневых методов сейчас является прямой корневой метод синтеза, называемый модальным методом синтеза системы по заданному качеству процесса управления.

Заданное качество системы будем определять желаемым расположением нулей и полюсов ее передаточной функции. Пусть задана передаточная функция замкнутой системы

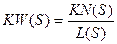(7.15)

где К - общий коэффициент усиления, N(s) и L(s) - много­члены, имеющие единичные коэффициенты при младших членах.

Передаточная функция замкнутой системы для управляемой величины по задающему воздействию g(t) имеет вид

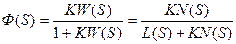(7.16)

или

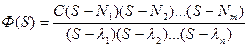. (7.17)

Задача синтеза состоит в том, чтобы, опираясь на ряд качественных показателей системы, найти соответствующее рас­положение величин λ₁, λ₂, …, λ_n на комплексной плоскости, а затем найти параметры корректирующих цепей, обеспечивающих заданное расположение указанных корней. При этом исходными качественными показателями могут быть, например, вид переходного процесса (апериодический, колебательный), время затухания, колебательность, частота колебании, интегральная квадратичная ошибка и т.д.

Указанные требования на одновременное выполнение раз­личных качественных показателей создаваемой системы приводят к задаче выделения на комплексной плоскости соответствующих областей допустимого расположения полюсов и нулей передаточ­ной функции замкнутой системы.

7.4. Прямой корневой метод синтеза САУ

по координатам пространства состояний

Пусть характеристическое уравнение, системы имеет вид

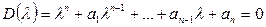(7.19)

Каждый коэффициент a_i (i=1, …, n) является функцией от не­которых параметров объекта управления и параметров корректирующих цепей, т.е.

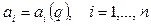, (7.20)

где q=[q₁, q₂, …]^T - искомый параметрический корректирующий вектор.

Для решения задачи модального синтеза введем желаемый характеристический многочлен

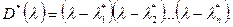
После раскрытия скобок получим

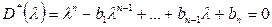(7.21)

где λ^*_i - желаемые значения корней характеристического много­члена, лежащие в заданных пределах:

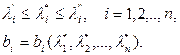(7.22)

Приравнивая соответствующие коэффициенты (7.20) и (7.22), получим

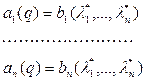(7.23)

Здесь имеем n уравнений с n неизвестными, решая которые непосредственно или численными интерационными методами, можно определить все n численных значении параметров корректирую­щего вектора q=[q₁, q₂, …]^T.

Очевидно, что полная коррекция, т.е. независимое назна­чение всех коэффициентов характеристического уравнения a_i (i=1, …, n) возможно только при числе корректирующих параметров не меньше n. Это обстоятельство дает возможность предписанного назначения желаемых корней λ^*_i (i=1, …, n).

Пример.

Для следящей системы, рассмотренной в 8.1, собственная скорректированная параметрическая матрица имеет вид

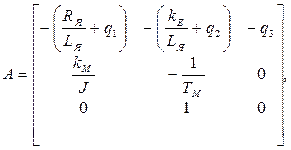
где

.

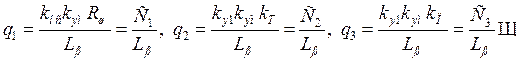Характеристическое уравнение системы будет

.

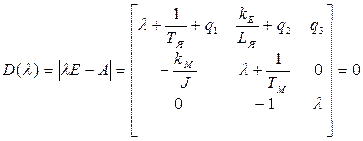После раскрытия определителя получим

l3+a₁λ²+a₂λ+a₃=0,

где

.

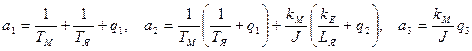Задаемся спектром матрицы А:

.

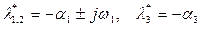После подстановки этих значении в уравнение

,

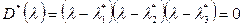получим желаемое характеристическое уравнение

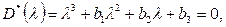
где

.

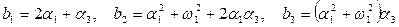В результате приравнивания коэффициентов характеристических уравнений проектируемой и желаемой систем будем иметь следу­ющие функции реализации:

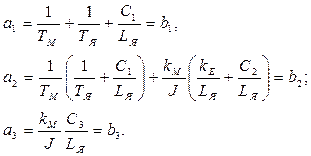
Отсюда следует возможность непосредственного решения задачи модального синтеза в виде

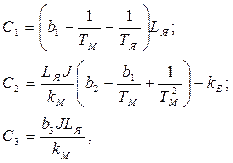
где C₁, C₂, C₃ - определяемые при синтезе коэффициенты передачи от измеряемых координат пространства состояний сис­темы, т.е. от тока в цепи якоря, от скорости вращения, от угла поворота исполнительного двигателя до входного напряжения цепи якоря.

7.5. Прямой метод синтеза корректирующей обратной

связи следящей системы

Пусть задана структурная схема следящей системы (рис. 8.8) и желаемое расположение корней характеристического уравнения замкнутой системы (рис. 7.9).

Передаточные функции неизменной части системы имеют вид

.

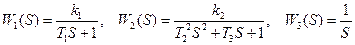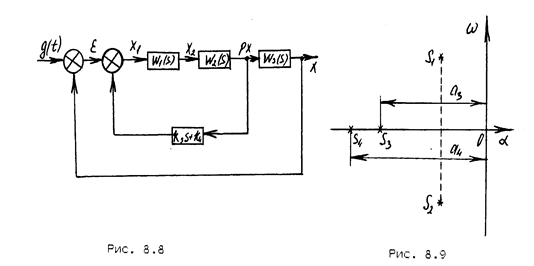
Требуется найти значения коэффициентов k₃ и k₄ дополни­тельной обратной связи, приводящие к желаемому расположению корней (рис.3.9), и коэффициент усиления прямой цепи системы k= k₁ k₂.

Согласно схеме имеем

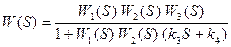
Следовательно

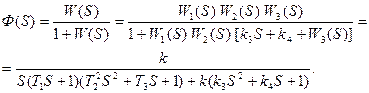
Отсюда характеристическое уравнение замкнутой системы имеет вид

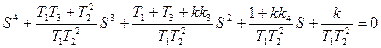(7.24)

Желаемому расположению корней соответствует следующее уравнение с заданными коэффициентами:

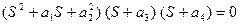
или

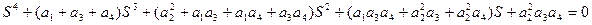
Приравнивая коэффициенты этого уравнения и уравнения 8.24, получаем соотношение

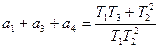(7.25)

и значения искомых коэффициентов

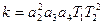
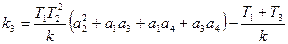
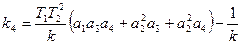
Условие (7.25) накладывает одну связь на произвольный выбор расположения корней – условие физической реализуемости в данной системе.

8. Системы автоматического управления

при случайных воздействиях