Уравнения (4.5) называются уравнениями возмущенного движения. Их тривиальные решения:
х1 = 0, …, х n = 0, (4.6)
при которых, как видно из (4.4), ук= у*к, называются уравнениям невозмущенного движения.
Начальные значения отклонения х к = х к0 называют возмущениями.
Решение системы уравнений (4.5) при некоторой заданной совокупности начальных условий называется возмущенным движением системы.
х к = fк (x10 , …, x n0, t). (4.7)
4.2. ОПРЕДЕЛЕНИЕ УСТОЙЧИВОСТИ ПО А.М. ЛЯПУНОВУ
Невозмущенное движение называется устойчивым по отношению к переменным ук, если при всяком заданном числе А, как бы мало оно ни было, можно выбрать другое положительное число λ (А) так, что для всех возмущений хк0, удовлетворяющее условию
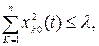
возмущенное движение (4.7) будет удовлетворять неравенству
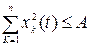 .
.
На рис. 4.2 показано геометрическое изображение условия устойчивости в пространстве трех переменных х1,х2, х3. геометрическая трактовка условия устойчивости по Ляпунову: если при возмущениях, выведших точку В0 (х10, х20, х30) за границу сферы λ, возмущенное движение будет таково, что точка не выйдет за границу сферы А, то оно устойчиво.
Если с течением времени возмущенное движение стремится к началу координат, то система асимптотически устойчива. При том 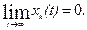
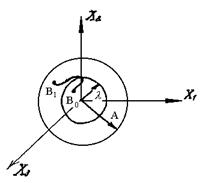
Рис. 4.2
Определение устойчивости по Ляпунову относится к движению, а не к системе. САУ может быть устойчива по отношение к одному движению и неустойчива по отношению к другому. Например, система регулирования скорости вала машины, устойчивая к изменению скорости, будет неустойчивойк изменению угла поворота. Но для краткости в дальнейшем будем говорить об устойчивых и неустойчивых САУ. Под устойчивостью САУ по существу подразумевается устойчивость процесса регулирования, т.е. устойчивость равновесия, или в более общем случае устойчивость частного решения дифференциального уравнения.
На практике при исследовании устойчивости реальных САУ часто пользуются линейными уравнениями, полученными в результате линеаризации, т.е. в результате отбрасывания членов, содержащих вторые и высшие степени, а также произведения отклонений переменных и их производных. В связи с этим возникают вопросы о возможности определения устойчивости реальных систем по их линеаризованным уравнениям.
Приведем интерпретацию теорем Ляпунова для линейных систем.
1. Линейная система устойчива, причем асимптотически, если все корни ее характеристического уравнения имеет отрицательные вещественные части.
2. Линейная система неустойчива, если среди корней ее характеристического уравнения есть хотя бы один корень с положительной вещественной частью.
3. Линейная система не асимптотически устойчива, если среди корней ее характеристического уравнения один нулевой, а у остальных отрицательные вещественные части.
С точки зрения дифференциальных уравнений в устойчивой линейной системе собственные колебания с течением времени затухают и полное движение стремится к вынужденному, т.е. решение дифференциального уравнения, определяющее возмущенное уравнение системы, стремится к частному решению. Это будет только в том случае, если корни рk характеристического уравнения Д(р)= 0 будут иметь отрицательные вещественные части, т.е.
рk= – dk ± iwk. (4.8)
Наличие одного нулевого корня в характеристическом уравнении приводит к тому, что с течением времени собственное движение стремится не к нулю, а к некоторой постоянной величине, зависящей от начальных условий.
Математическая формулировка условий, которым должны удовлетворять коэффициенты характеристического уравнения устойчивой системы, или другие формы выражения условий устойчивости, называется критериями устойчивости.
На практике применяет в основном алгебраические и частотные критерии устойчивости, в том числе критерии Рауса, Гурвица, Вышнеградского, Михайлова, Найквиста и др.
Все эти критерии позволяют исследовать устойчивость линейных замкнутых систем регулирования, не прибегая к решению уравнений и к определению корней характеристического уравнения.
3. КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА
Алгебраический критерий Гурвица позволяет судить об устойчивости линейной системы по коэффициентам характеристического уравнения замкнутой системы
Д (р)= аnрn+ аn-1 рn-1+…+ а1 р+ а0=0 (4.9)
Нетрудно показать, что левым корням характеристического уравнения (4.9) соответствуют положительные коэффициенты, аn, аn-1,..., а1, а0. Для этого уравнение (4.9) можно представить в виде произведения простых сомножителей
Д (р)= аn(р – р1)(р – р2)…(р – рn)=0, (4.10)
подставить в него корни
рk= – dk ± iwk (4.11)
и, раскрыв скобки, привести его к виду (4.9).
Таким образом, необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения системы. Однако это условие не является достаточным. Критерий Гурвица позволяет сформулировать необходимое и достаточное условие устойчивости.
Для того, чтобы система была устойчивой, необходимо и достаточно, чтобы старший определитель Гурвица 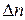 и все его диагональные миноры были бы положительные.
и все его диагональные миноры были бы положительные.
Правило образования определителя Гурвица сводится к следующему. В верхней строке записываются по порядку коэффициенты с нечетными индексами, начиная с аn-1.. Всего заполняется n элементов строки, взамен недостающих коэффициентов ставятся нули. Вниз от элементов i -ой строки столбцы определителя заполняются коэффициентами с индексами, возрастающими каждый раз на единицу.
Старший определитель Гурвица, составленный по этому правилу на основании уравнения (4.9), имеет вид
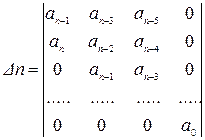 .
.
Для обеспечения устойчивости системы необходимо и достаточно выполнение следующих условий:
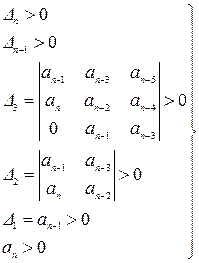 (4.12)
(4.12)
Подучим условия устойчивости по критерию Гурвица для некоторых частных случаев.
1. Система 1-го порядка. Характеристическое уравнение в этом случае имеет вид
Д (р)= а1 р + а0=0.
Условия устойчивости (4.12) сводятся к выполнению следующих неравенств: 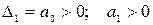 .
.
2. Система 2-го порядка. Старший определитель Гурвица, составленный по характеристическому уравнению
Д (р)=а2р2+ а1 р+ а0=0,
принимает вид
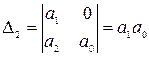 . (4.13)
. (4.13)
Условия устойчивости (4.12) сводятся к выполнению следующих неравенств:
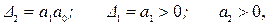
т.е. система будет устойчива, если
а2>0; а1>0; а0>0.
Таким образом, необходимым и достаточным условием устойчивости систем 1-го и 2-го порядков является положительность коэффициентов их характеристических уравнений.
3. Система 3-го порядка. Старший определитель Гурвица, составленный по характеристическому уравнению
Д (р)=а3р3+ а2 р2 + а1 р+ а0,
принимает вид
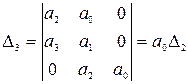 ,
,
где
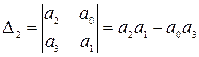 . (4.14)
. (4.14)
Условие устойчивости (4.12) в этом случаев сводится к выполнению следующих неравенств:
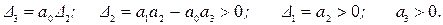
Таким образом, кроме положительности коэффициентов а3>0; а2>0; а1>0; а0>0
для обеспечения устойчивости системы 3-го порядка необходимо выполнение следующего дополнительного условия:
а2а1– а0а3 > 0. (4.15)
Для уравнений более высоких степеней пользоваться критерием Гурвица нецелесообразно, так как процесс раскрытия определителей высокого порядка становится неоправданно трудоемким, а дополнительные условия устойчивости получаются громоздкими. При неоднократных попытках предложить более простые методы раскрытия определителей авторы приходили к алгоритму Рауса или очень близкому к нему алгоритму.
ЛЕКЦИЯ 10
План лекции:
1. Критерий Михайлова.
2. Критерий Найквиста.
3. Рекомендуемая литература [1, 4, 8].
4.4. КРИТЕРИЙ МИХАЙЛОВА
Критерий Михайлова относится к графическим критериям. Он позволяет судить об устойчивости САУ любого порядка по годографу характеристического многочлена
Д(р)=аnрn+…+а1р+а0=аn(р-р1)(р-р2)…(р-рn), (4.16)
который при p=iw можно представить в виде
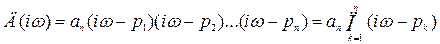 . (4.17)
. (4.17)
Каждый сомножитель (iw - рk) многочлена Д(iw) можно представить на плоскости комплексного переменного в виде вектора.
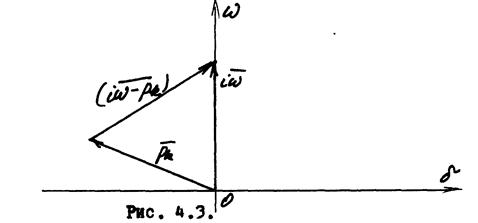
Из рис. 4.3. видно, что если корни рk имеет отрицательные вещественные части pk=-dk± iwk, т.е. векторы рk расположены слева от мнимой оси комплексной плоскости, то при изменении частоты w = -¥ ¸ ¥ каждый из векторов 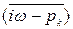 опишет угол против часовой стрелки (в положительном направлении), равный 1800. Следовательно, вектор характеристического уравнения
опишет угол против часовой стрелки (в положительном направлении), равный 1800. Следовательно, вектор характеристического уравнения
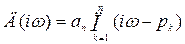
в этом случае опишет угол (180 n)°. Это и есть критерий устойчивости Михайлова.
Чтобы воспользоваться этим критерием, годограф характеристического уравнения, который описывает вектор Д(iw), целесообразно строить в координатах V(w) и U(w):
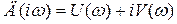 .
.
Учитывая симметричность годографа относительно действительной оси (функция U(w) – четная), можно ограничиться построением лишь одной его половины, например, при изменении w от 0 до ¥. Условие устойчивости в этом случае можно сформулировать следующим образом: чтобы система была устойчивой, необходимо и достаточно, чтобы вектор характеристического уравнения Д(iw) при изменении w от 0 до ¥ повернулся в положительном направлении на угол (90 n)° (рис. 4.4).
При w=0 нечетная функция V(w)=0, а U(w)=а0, причем а0>0. Учитывая это, критерий Михайлова можно сформулировать следующим образом.
Чтобы система была устойчивой, необходимо и достаточно, чтобы годограф характеристического уравнения Д(iw), начинаясь при w=0 на положительной полуоси U(w), при возрастании частоты от 0 до ¥ прошел последовательно в положительном направлении n квадрантов координатной плоскости.
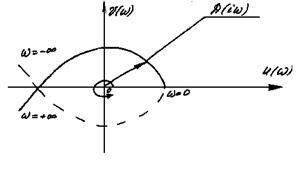
Рис. 4.4
На рис.4.5 показаны кривые Михайлова (годографы вектора Д(iw)) для устойчивых систем от 1-го до 5-го порядка.
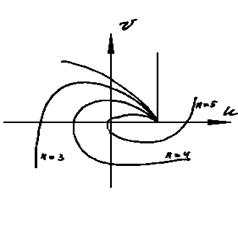
Рис. 4.5
На рис. 4.6 показаны кривые Михайлова неустойчивых систем: а) а0<0;
б) вектор Д(iw) поворачивается по часовой стрелке; в) порядок уравнения n =5, а кривая Михайлова находится в одном квадранте; г) нарушается последовательность прохождения квадрантов; д) система находится на границе устойчивости, т.к. кривая Михайлова проходит через начало координат; е) система неустойчива, т.к. кривая Михайлова проходит через начало координат и не последовательно пересекает квадранты.
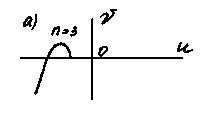
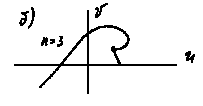
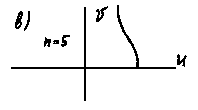
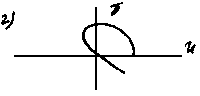
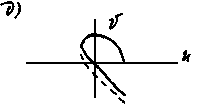
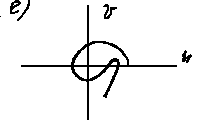
Рис. 4. 6
Рассмотрим одно из следствий критерия Михайлова-условие перемежаемости корней действительной U(w) и мнимой V(w) частей функции Д(iw).
При последовательном прохождении кривой Михайлова квадрантов координатной плоскости действительная U(w) и мнимая V(w) оси пересекаются поочередно. Отсюда следует, что действительная и мнимая функции при возрастании w обращаются в нуль поочередно, т.е. корни их вещественны и перемежаются.
На рис. 4.7 а приведен пример графиков для устойчивой системы (кривые U и V пересекают ось w поочередно); на рис. 4.7 б для неустойчивой системы (очередность пересечения кривыми U и V оси w нарушена).
Условие перемежаемости корней показывает, что для суждения об устойчивости системы не обязательно точно вычерчивать всю кривую, достаточно определить ее ход лишь вблизи точек пересечения с координатными осями.
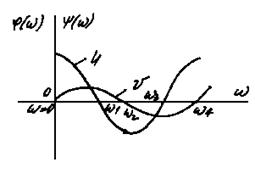
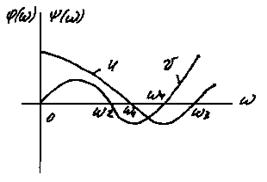
а б
4.5. КРИТЕРИЙ НАЙКВИСТА
Частотный критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике разомкнутой системы W(iw), которая строится в координатах действительной 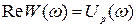 и мнимой
и мнимой 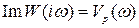 частей АФЧХ (рис.4.8).
частей АФЧХ (рис.4.8).
Чтобы определить условие устойчивости по критерию Найквиста, необходимо найти связь между функциями W(iw) и Д(iw). Для этого рассмотрим функцию
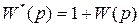 , (4.18)
, (4.18)
представляющую собой знаменатель передаточных функций замкнутой системы.
Передаточную функцию разомкнутой системы W(р) можно представить в виде отношения двух многочленов
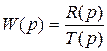 , (4.19)
, (4.19)
где Т(р) часто называют характеристическим многочленом разомкнутой системы. С учетом (4.19) выражение (4.18) можно представить в следующем виде:
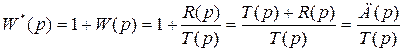 , (4.20)
, (4.20)
где Д(р)=Т(р)+R(р) - характеристический многочлен замкнутой системы, причем порядок многочлена Д(р) определяется порядком многочлена Т(р) и равен n.
Заменяя р на iw, будем иметь
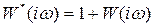 , (4.21)
, (4.21)
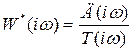 . (4.22)
. (4.22)
Анализ (4.21) показывает, что вектор W*(iw) смещен на единицу по отношению к вектору W (iw). Причем, они описывают один и гот же годограф – АФЧХ разомкнутой системы W(iw) (рис. 4.9). Эго позволяет условие устойчивости связать как с поведением вектора W(iw), так и вектора W*(iw).
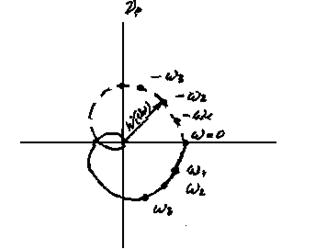
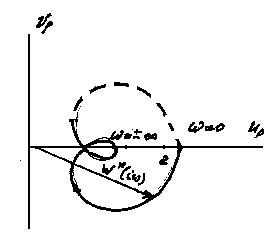
Рис. 4.8 Рис. 4.9
На основании (4.22) можно записать
arg W*(iw)= arg Д (iw)-arg Т (iw). (4.23)
При изменении частоты w от - ¥ до + ¥ для обеспечения устойчивости системы в соответствии с критерием Михайлова
arg Д (iw)=180о×n. (4.24)
Следует иметь в виду, что устойчивая замкнутая система может оказаться неустойчивой в разомкнутом состоянии, поэтому характеристическое уравнение разомкнутой системы Т(р)=0 может иметь корни с положительными действительными частями (правые корни). Положим, что уравнение Т (р)=0 имеет r правых корней и (n-r) левых, тогда в соответствии c рис. 4.4. вектор Т (iw) при изменении частоты от - ¥ до + ¥ опишет угол в положительном направлении 180о(n-r) и в отрицательном -180or, т.е.
arg Т (iw)=180о(n-r)-180or=180оn-360or. (4.25)
С учетом (4.24) и (4.25) уравнение (4.23) принимает вид
arg W*(iw)=180оn-180оn+360or=360or. (4.26)
Учитывая симметричность АФЧХ относительно действительной оси (Up(w) –функция четная), условие (4.26) можно переписать в виде
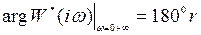 . (4.27)
. (4.27)
Отсюда вытекает формулировка критерия Найквиста.
Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении частоты w от 0 до ¥ вектор W*(iw) повернулся в положительном направлении на угол 1800r, где r - число правых корней характеристического многочлена разомкнутой системы, т.е. чтобы АФЧХ разомкнутой системы W(iw) охватила точку (-1, 0×i) в положительном направлении r/2 раз.
Если разомкнутая система устойчивая, то r=0 и условие (4.27) принимает вид
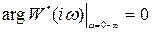 , (4.28)
, (4.28)
т.е. суммарный угол поворота вектора W*(iw) вокруг начала координат должен равняться нулю. Это будет в том случае, когда АФЧХ не охватывает точку (-1, 0×i) т.е. пересекает действительную ось в диапазоне (0¸ -1).
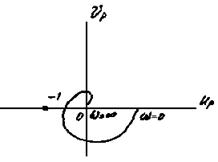
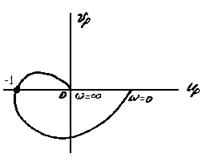
Условие устойчивости в этом случае можно сформулировать следующим образом. Для того чтобы замкнутая система была устойчива в случае устойчивой разомкнутой системы, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку (-1, 0×i), т.е. пересекала бы действительную ось правее этой точки (рис. 4.10 а).
Если АФЧХ пересечет действительную ось в точке (-1, 0×i), то соответствующая ей система будет находиться на границе устойчивости (рис.4.10 в). Случай показанный на рис. 4.10 г, соответствует неустойчивой системе.
Для систем высокого порядка могут возникнуть затруднения при определении угла, на который поворачивается вектор W*(iw). В этом случае для суждения об устойчивости, можно рекомендовать следующую интерпретацию критерия Найквиста, предложенную Я.З. Цыпкиным.
 а
а 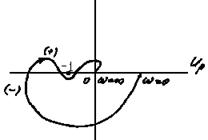 б
б
 в
в 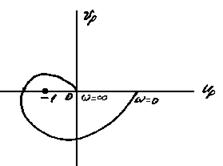 г
г
Рис. 4. 10
Система будет устойчивой, если разность между числом положительных и отрицательных переходов АФЧХ W(iw) через отрезок действительной оси (-¥¸ -1) при изменении w от 0 до ¥ будет равна r, где r - число правых корней характеристического уравнения разомкнутой системы.
При этом переход АФЧХ через действительную ось сверху вниз считается положительным, снизу вверх - отрицательным.
Разность положительных и отрицательных переходов АФЧХ действительной оси Up в диапазоне (-¥¸ -1) (рис.4.10 б) равна нулю, следовательно, замкнутая система, соответствующая этому случаю, будет устойчива.
Для астатических систем характеристический многочлен разомкнутой системы Т(р) имеет нулевые корни Т (р)=рn×Т*(р), т.е. передаточная функция разомкнутой системы в этом случае принимает вид
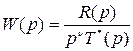 , (4.29)
, (4.29)
где n - порядок астатизма.
Заменяя в выражении (4.29) р на iw, получим
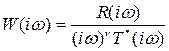 (4.30)
(4.30)
Анализ (4.30) показывает, что при w=0 АФЧХ разомкнутой системы W(iw) терпит разрыв. Чтобы избежать неопределенности в точке разрыва при построении АФЧХ разомкнутой системы, условились обходить начало координат в плоскости комплексного переменного справа по дуге бесконечно малого радиуса r (рис.4.11).
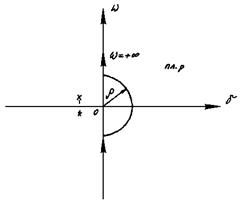
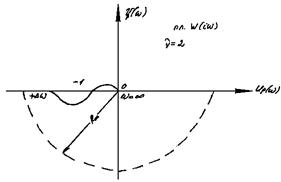
Рис 4.11 Рис. 4.12
Из выражения (4.30) следует, что при изменении частоты w в окрестности нуля (w=-Dw ¸ +Dw) АФЧХ разомкнутой астатической системы можно представить в виде дуги, которую описывает бесконечно большой радиус R¥. При этом в диапазоне w = +Dw ¸ +¥ АФЧХ разомкнутой астатической системы строится обычным методом, а затем дополняется дугой, которую должен описать радиус, вращаясь по часовой стрелке на угол (90ν)°.
Определение устойчивости по АФЧХ разомкнутой астатической системы, дополненной дугой бесконечно большого радиуса, ведется точно так же, как и для статических систем.
На рис. 4.12. показана АФЧХ устойчивой системы при наличии астатизма второго порядка.
Рассмотренные особенности применения критерия Найквиста для астатических систем можно распространить и на случай, когда характеристическое уравнение разомкнутой системы имеет чисто мнимые корни ± iw1. В отличие от предыдущего случая наличие в уравнении Т(р)=0 мнимых корней связано с разрывом W(iw) при w =± iw1.
ЛЕКЦИЯ 11
План лекции:
1. Определение устойчивости по ЛАФЧХ.
2. Д - разбиение в плоскости комплексного параметра.
4. Рекомендуемая литература [1, 3, 8].
4.6. СУЖДЕНИЕ ОБ УСТОЙЧИВОСТИ ПО ЛАФЧХ
РАЗОМКНУТОЙ СИСТЕМЫ
По построенным логарифмическим амплитудным и фазовым характеристикам разомкнутой системы также можно судить об устойчивости замкнутой системы. Для этого надо установить соответствие между некоторыми свойствами ЛАЧХ и амплитудно-фазовой характеристики. Рассмотрим только системы, устойчивые в разомкнутом состоянии.
Как установлено выше, "опасным" для устойчивости САУ является отрезок отрицательной вещественной полуоси от –¥ до – 1.
Когда амплитудно-фазовая характеристика пересекает отрицательную вещественную полуось, логарифмическая фазовая характеристика пересекает одну из линий –p, -3p и т.д. Переходы через эти линии не опасны, если они совершаются справа от точки (– 1, i×0), т.е. если модуль 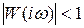 и, следовательно, если ординаты ЛАЧХ
и, следовательно, если ординаты ЛАЧХ 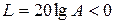 , т.е. отрицательны при j = – p.
, т.е. отрицательны при j = – p.
Положительному переходу (сверху вниз) через отрезок (–¥, – 1 ) характеристик 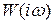 соответствует переход фазовой характеристики
соответствует переход фазовой характеристики 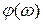 через одну из линий –p, -3p,... снизу вверх (тоже положительный переход). Отрицательному переходу
через одну из линий –p, -3p,... снизу вверх (тоже положительный переход). Отрицательному переходу 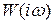 также соответствует отрицательный переход ЛФЧХ. Отсюда вытекает следующее положение: если разомкнутая система устойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы во всех областях положительных ЛАЧХ разность между числом положительных и отрицательных переходов ЛФЧХ через линии –p, -3p,... равнялась нулю.
также соответствует отрицательный переход ЛФЧХ. Отсюда вытекает следующее положение: если разомкнутая система устойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы во всех областях положительных ЛАЧХ разность между числом положительных и отрицательных переходов ЛФЧХ через линии –p, -3p,... равнялась нулю.
Очевидно, если разомкнутая САУ неустойчива и ее характеристическое уравнение имеет r правых корней, то для устойчивости замкнутой САУ разность между положительными и отрицательными переходами ЛФЧХ через (–180)° на тех частотах, на которых ЛАЧХ положительна, должна равняться r / 2.
На рис. 4.13 показаны примеры АФЧХ и соответствующие им ЛАФЧХ разомкнутой системы. При этом предполагается, что разомкнутая система устойчива. Исследование проводится в области положительных ординат ЛАЧХ. Пересечение АФЧХ 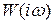 с кругом единичного радиуса соответствует пересечение ЛАЧХ с осью частот.
с кругом единичного радиуса соответствует пересечение ЛАЧХ с осью частот.
На рис. 4.13 а,в показаны характеристики систем, устойчивых в замкнутом состоянии, на рис. 4.13 б,г - характеристики неустойчивых систем.
На рис. 4.14 а показаны запасы устойчивости по амплитуде 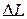 и по фазе
и по фазе 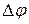 . Запас устойчивости по амплитуде определяется значением ЛАЧХ на частоте пересечения ЛФЧХ прямой, проходящей через (-180)°. Запас устойчивости по фазе
. Запас устойчивости по амплитуде определяется значением ЛАЧХ на частоте пересечения ЛФЧХ прямой, проходящей через (-180)°. Запас устойчивости по фазе 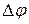 определяется как превышение ЛФЧХ над прямой (-180)° на частоте среза. Частотой среза называют частоту, на которой ЛАЧХ пересекает ось частот, т.е.
определяется как превышение ЛФЧХ над прямой (-180)° на частоте среза. Частотой среза называют частоту, на которой ЛАЧХ пересекает ось частот, т.е. 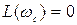 (на частоте среза САУ не искажает входной сигнал по амплитуде).
(на частоте среза САУ не искажает входной сигнал по амплитуде).
Если запасы устойчивости 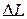 и
и 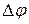 равны нулю, то система находится на границе устойчивости. Чем больше значения
равны нулю, то система находится на границе устойчивости. Чем больше значения 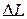 и
и 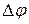 , тем дальше от границы устойчивости находится система. Тем не менее, стремиться к неограниченному увеличению
, тем дальше от границы устойчивости находится система. Тем не менее, стремиться к неограниченному увеличению 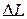 и
и 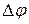 не следует, так как увеличение запасов устойчивости обычно связано с уменьшением коэффициента передачи системы и, следовательно, с увеличением статических ошибок и ухудшением качества регулирования (в частности, с увеличением времени переходного процесса).
не следует, так как увеличение запасов устойчивости обычно связано с уменьшением коэффициента передачи системы и, следовательно, с увеличением статических ошибок и ухудшением качества регулирования (в частности, с увеличением времени переходного процесса).
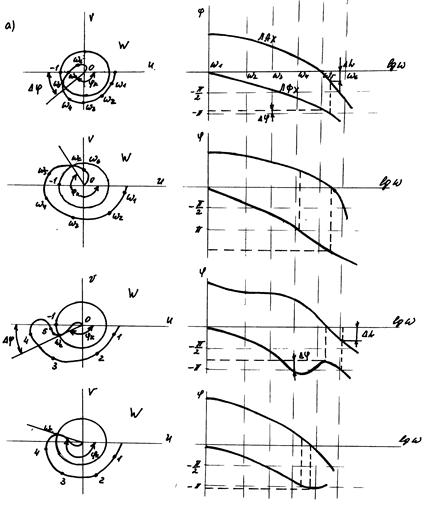
Рис. 4.13
Поэтому при проектировании САУ запасы устойчивости необходимо выбирать таким образом, чтобы исключить возможность потери устойчивости при случайном изменении параметров и режимов работ системы, и в то же время обеспечить требование к качеству и ошибкам регулирования. Например, рекомендуют выбирать запасы устойчивости по амплитуде 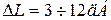 и по фазе
и по фазе 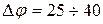 .
.
 2014-02-02
2014-02-02 1023
1023








