Тема 2.2 Метод граничных элементов

Лекция 10

Сходимость, аппроксимация и устойчивость разностных схем.

Решение одномерных нестационарных задач

Решение одномерной линейной задачи с краевым условием второго рода

В реальных задачах одно или несколько краевых условий часто могут быть выражены через производную (краевые условия Неймана).

Часто при работе с математическими моделями приходится исследовать зависимость параметров системы от времени. Такой класс задач называется нестационарные. Существует два способа получения решения: явный и неявный метод. При использовании любого из способов нам надо принять шаблон для замены частных производных на разностные аналоги.

LV+P=0 исходный дифференциальный оператор

L^hV^h+p^h=0 разностный оператор. h – шаг сетки

|| V^(h)-V^h ||≤c_1*h^k – сходимость порядка К. Разностная схема аппроксимируется с точностью К.

с₁=Const, не зависит от h

Аппроксимация

L^hV(h)+p^h=δ^h<o:p</o:p

Если норма невязки || δ^h || ≤ c_2*h^k – имеет место аппроксимация порядка К.

Устойчивость к возмущению

L^hV^h+p^h=0

L^hZ^h+p^h=ε^h

Приводятся фундаментальные решения для ортотропных и анизотропных областей и показывается, что все положения, обсуждавшиеся в предыдущих разделах, справедливы также и для бесконечных областей при выполнении определенных условий регулярности на бесконечности. Привлечение подходящего фундаментального решения, удовлетворяющего части граничных условий рассматриваемой задачи, позволяет снизить объем вычислительной работы. И наконец, "описываются специальные численные процедуры для общего вида трехмерных и осесимметричных задач.

"•

Рис. 1. Граничные элементы (а— постоянные; б— линейные; в— квадратичные).

Функции и и q имеют постоянные значения в области каждого элемента и

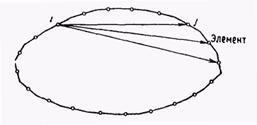
Рис. 2. Схема связи между фундаментальным решением в граничном узле i и граничными элементами.