Введение. В этой главе исследуется приложение метода граничных интегральных уравнений к уравнению теплопроводности

В этой главе исследуется приложение метода граничных интегральных уравнений к уравнению теплопроводности

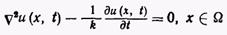(1)

с граничными условиями следующего типа:

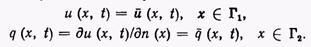(2)

Коэффициент k в уравнении (4.1) может принимать различные значения в зависимости от рассматриваемой физической задачи и считается независимым как от координат, так и времени. Поскольку рассматриваемая задача зависит от времени, необходимо задать некоторые начальные условия в момент времени t = t_Q:

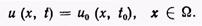(3)

Задаче, описываемой уравнением (1), граничными условиями (2) и начальным условием (3), можно придать форму интегрального уравнения относительно неизвестной функции и, и для выполнения этого преобразования могут быть использованы различные приемы. Один из них был предложен в 1970 г. Риццо и Шиппи, которые применили прямую формулировку метода граничных элементов в сочетании с преобразованием Лапласа к решению задач неустановившейся теплопроводности. В предположении, что все входящие в задачу функции допускают преобразование Лапласа, граничное интегральное уравнение записывалось и решалось в пространстве изображений для последовательности действительных положительных значений параметра преобразования. Затем применялась численная процедура обратного пре­образования для нахождения значений неизвестных в действительном пространстве. При использовании такого подхода временная зависимость задачи на какой-то период устранялась и вместо исходного уравнения параболического типа решалось более удобное уравнение в частных производных эллиптического типа. Баттерфилд и Томлин применили непрямую формулировку (с использованием источника), рассмотрев среду с ортотропными областями, встречающуюся в механике грунтов. Решение для неустановившегося случая было получено распределением мгновенных источников в рассматриваемой области в начальный момент времени, с тем чтобы воспроизвести заданное начальное условие, и заданием на внешней и внутренних границах непрерывных функций источников, удовлетворяющих заданным условиям на внешней границе и на границах раздела.

Чанг, Канг и Чен использовали зависящие от времени фундаментальные решения в сочетании с прямым методом решения двумерных задач теплопроводности как в изотропной, так и в анизотропной средах. Дискретное представление граничного интегрального уравнения было выполнено с постоянными шагами по пространственным и временной координатам. Аналогичный подход к решению трехмерных задач использовал Шоу, который в основном рассмотрел аналитические, а не численные аспекты метода. Этот прием обсуждался впоследствии Вроубелом и Бреббия, исследовавшими возможность включения в рас­смотрение интерполирующих функций высокого порядка от пространственных и временной переменных и тем самым рассмотрения более важных с практической точки зрения задач. Они также исследовали численную процедуру для решения неустановившихся осесимметричных задач, где из-за сложности получения фундаментального решения потребовалось ввести разложение в ряды и аналитически вычислять интегралы по времени, входящие в граничное интегральное уравнение.

Иной подход, основанный на использовании комбинации методов граничных элементов и конечных разностей при решении нестационарных задач, был предложен Бреббия и Уокером. Здесь производная по времени аппроксимировалась конечными разностями, и для нахождения зависимости решения от времени использовалась шаговая процедура конечно-разностного типа.

Все упомянутые выше численные схемы рассматриваются ниже, где также приведены основные процедуры для их численной реа­лизации применительно к двумерным задачам. Хотя обсуждаются в основном задачи для конечной однородной изотропной среды, рассмотрены также задачи с внутренними источниками, кусочной неоднородностью среды, ортотропией и анизотропией, бесконечными или полубесконечными областями — все это делается точно так же, как и в гл. 2 для задач о потенциале.

Затем кратко обсуждаются трехмерные задачи и несколько более подробно описано приложение к асимметричным случаям. Зависящее от времени фундаментальное решение для осесимме-тричного случая получается непосредственно из решения для трехмерной задачи, и представлена процедура численного решения уравнения (1) для осесимметричной области.