Преобразование Лапласа

Введем следующее обозначение преобразования Лапласа для функции и (х, t), для которой это преобразование допускается:

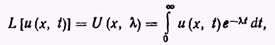(4)

и предположим, что параметр преобразования X — действительное положительное число.

Интегрируя по частям, можно показать, что

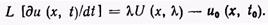(5)

Уравнение (1) после выполнения преобразования принимает вид

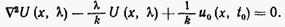(6)

Граничные условия (2) также следует преобразовать в соответствии с формулой (4.4), полагая для простоты, что они не зависят от времени, и получая в результате

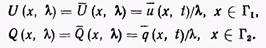(7)

Аналогично находим и преобразование Лапласа для уравнения взвешенных невязок

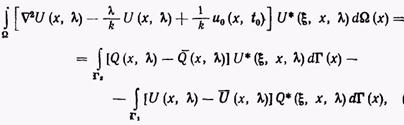(8)

где Интегрируя оператор Лапласа дважды по частям, получим

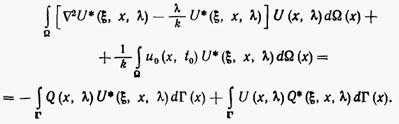(9)

Полагая фундаментальным решением уравнения (6), удовлетворяющим равенству

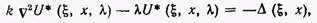(10)

из уравнения (9) найдем

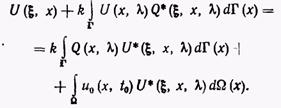(11)

Фундаментальное решение U* для трехмерных задач имеет вид

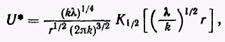(12)

а для двумерных задач —

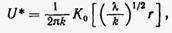(13)

где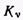— модифицированная функция Бесселя второго рода порядка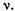

Исследуем особенности записанных выше фундаментальных решений. При U0 к нулю стремится и аргумент модифицированных функций Бесселя. Предел функци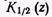и при 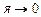имеет вид

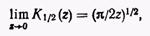(14)

что дает

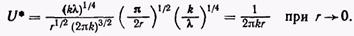(15)

Отсюда следует, что фундаментальное решение уравнения (6) имеет особенность того же типа, что и фундаментальное решение исходного уравнения Лапласа.

Аналогично получаем предел функции:

(16)

откуда имеем

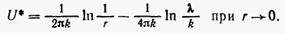(17)

Первое слагаемое в правой части этого выражения представляет собой фундаментальное решение для двумерного уравнения Лапласа, тогда как второе слагаемое является некоторой постоянной.

Считая точку £ в уравнении (11) принадлежащей границе и учитывая, что интеграл от функции Q* имеет разрыв, когда точка | находится на границе Г, получим уравнение

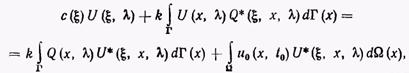(18)

где коэффициент с имеет то же значение, что и раньше.

В дискретной форме это уравнение решается численно для последовательности N выбранных значений параметра преобразования, задаваемых достаточно произвольно. Отметим, что наличие специальных начальных условий приводит к интегралу по области Q. Один путь вычисления этого интеграла состоит в разбиении всей области на ячейки и численном интегрировании по каждой из них. Однако если функция и₀ удовлетворяет уравнению Лапласа, то интеграл по области в уравнении (18) можно преобразовать в эквивалентные граничные интегралы. Каким бы ни был метод вычисления интеграла по области, этот интеграл уже не вводит дополнительной неизвестной, поскольку функция и₀ задается, а уравнение (18) по-прежнему остается граничным интегральным уравнением.

Последним этапом является обратное преобразование решения, которое выполняется численно. Следуя, например, методу Шапери, предположим, что функция и в любой точке может быть представлена в виде бесконечного ряда

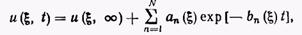(19)

где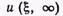— стационарное решение, а_п и b_п — функции пространственных координат. Применяя к представлению (19) преобразование Лапласа, получим

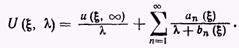(20)

Значения коэффициентов b_n полагаются равными предварительно выбранным значениям А,. Таким образом, остается определить N значений коэффициента а в каждой граничной точке (плюс в каждой внутренней точке, в которой требуется знать решение). Решения уравнения (18) дают N значений функции U в каждой точке, что позволяет с помощью выражения (20) определить коэффициенты а_n и, следовательно, с помощью выражения (19) найти значения физической величины U. Аналогичные расчеты требуется проводить и при определении действительных значений внутренних и граничных потоков.

Отметим, что обратное преобразование по существу представляет собой процесс аппроксимации кривой, и раз так, то в процессе численного решения важно знать ожидаемый характер поведения решения, с тем чтобы подобрать значения параметра преобразования Я,, поскольку, выбрав слишком много значений, можно сделать неустойчивым процесс нахождения решения с помощью выражения (20), тогда как выбор слишком малого числа значений не позволит с достаточной точностью аппроксимировать кривую.